Concept 34.2: Neurons Generate Electric Signals by Controlling Ion Distributions

The one feature common to all nervous systems is that they encode and transmit information in the form of action potentials. Some basic electrical principles help us understand how neurons produce action potentials and other electric signals. Current is a flow of electric charges from place to place. In a wire, electrons flow, and current is based on the flow of electrons. However, in the cells of organisms, current is based on the flow of ions in solution (see Concept 2.2), such as sodium ions (Na⁺), potassium ions (K⁺), or chloride ions (Cl⁻). Each Na⁺ ion, for example, bears a single positive charge. When Na⁺ ions move from one place to another, positive charges flow, and this flow of charges is an electric current.

A voltage, also called an electric potential difference, exists if positive charges are concentrated in one place and negative charges are concentrated in a different place. Voltages produce currents because opposite charges attract and will move toward one another if given a chance. To illustrate, suppose positively charged ions are concentrated in one area and negatively charged ions are concentrated in another. Positive ions such as Na⁺ will be attracted to and tend to flow toward the negative area, giving rise to a current.

Of all the background information that is helpful for understanding the electrical function of neurons, the locations where voltage differences can exist are most important.

• No voltage differences exist from one place to another within open solutions such as the intracellular fluids of a cell. In an open solution, positive and negative ions distribute themselves evenly so that there are no charge imbalances.
• Voltage differences exist only across membranes such as the cell membrane. A cell membrane is composed primarily of lipids (see Figure 5.1). Because ions have an electric charge, they tend to associate with water, not lipids, because water molecules are polar (see Concept 2.2). Moreover, the lipid molecules in a membrane, being hydrophobic, tend to associate with each other rather than with water or ions. Because of these principles, ions tend to remain in the aqueous solutions on either side of a membrane and do not readily cross the membrane. Consequently, positive ions may be concentrated on one side of a cell membrane while negative charges are concentrated on the opposite side.

Solutions that are not immediately in contact with a membrane are termed bulk solutions. We can summarize by saying that a bulk solution is electrically neutral and does not show charge differences from place to place, but a membrane may have a charge difference across it, caused by ion imbalances in the water immediately next to the membrane surfaces:

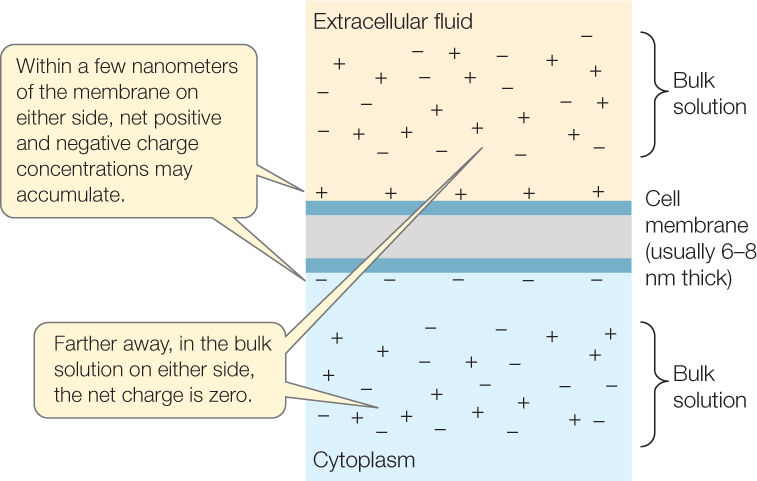
A voltage exists across a membrane that has a charge difference from one side to the other. This voltage (potential difference) is called the membrane potential and can be readily measured (FIGURE 34.4). A neuron is described as “resting” when it’s not carrying a signal. In a resting neuron, the membrane potential is referred to as the resting potential and is typically between −60 and −70 millivolts (mV). The minus sign means that the inside of the cell is electrically negative relative to the outside. Membrane potentials are always written in this way: the sign (negative or positive) always refers to the charge inside relative to the charge outside.

RESEARCH TOOLS

Figure 34.4: Measuring the Membrane Potential An electrode can be made from a fine glass tube with a sharp tip filled with a solution that conducts electric charges. When such an electrode is inserted into an axon and another electrode is placed in the extracellular fluid just outside the axon, the difference in voltage across the axon cell membrane—called the membrane potential—can be measured.

Like other cell membranes, neuron cell membranes contain proteins that serve as ion transporters and channels (see Concept 5.2). Ions cannot pass through the membrane lipid bilayer, as we have just emphasized, and this permits charge differences to exist across a neuron cell membrane. However, ions can pass through the transporters and channels in the membrane. The transporter proteins and channel proteins determine the magnitudes and directions of the voltages and currents across the membrane.

Only small shifts of ions are required for rapid changes in membrane potential

As we talk in this chapter about the functions of neurons, we will often encounter cases in which rapid changes of the membrane potential are of critical importance. We need, therefore, to focus briefly on some key properties of these changes.

The membrane potential changes when ions are redistributed. During the rapid events of routine electrical signaling such as action potentials, ion redistribution occurs through membrane channel proteins. Channels are proteins that permit ions to cross the membrane by simple diffusion (see Concept 5.2).

Suppose that a membrane shifts from being negative on the inside to being positive on the inside. Suppose also that this change occurs because channels in the membrane allow a current of positive charges (ions) to flow inward across the membrane.

A critically important point is that only relatively small numbers of positive charges need to move through the membrane for this change of membrane potential to occur. This is true because only the charges within a few nanometers of the membrane surfaces are changing. Robert Schmidt and his colleagues once asked, Of all the ions within 1,000 nanometers of a membrane surface, what proportion are responsible for the membrane potential? Their answer was less than 100 out of every 1 million. Just a relatively few ions—positioned within a few nanometers of the membrane surfaces—are involved in rapid changes of membrane potential. The other ions, located in the bulk solutions on either side, are not directly involved.

Similarly, the current through the membrane moves only relatively small numbers of ions during rapid changes of membrane potential. The current is not changing the compositions of the bulk solutions: the compositions of the intracellular and extracellular fluids. A small current is sufficient to redistribute ions on the inner and outer membrane surfaces and lead to a large change in membrane potential—a phenomenon that is fundamental to how neurons generate signals.

The sodium–potassium pump sets up concentration gradients of Na⁺ and K⁺

One of the key membrane proteins is a transporter called Na⁺-K⁺-ATPase or the sodium–potassium pump. The protein goes through repeating cycles in which it actively transports ions. During each cycle, it uses the energy of an ATP molecule to expel three Na⁺ ions from inside the neuron and to pump two K⁺ ions into the neuron from the outside. Na⁺ and K⁺ are the principal positive ions in both the intracellular and extracellular fluids.

The sodium–potassium pump creates steady ion concentration differences between the intracellular and extracellular fluids. Because of it, the concentration of Na⁺ is higher in the bulk fluids outside the neuron than inside, and the K⁺ concentration is higher in the bulk fluids inside than outside.

The resting potential is mainly a consequence of K⁺ leak channels

What is the cause of the resting potential? This voltage difference is principally the result of K⁺ channels that are open all the time. As we have seen, K⁺ is more concentrated inside a neuron than outside. Some (fewer than half) of the K⁺ channels—channels that specifically permit K⁺ to diffuse through the neuron cell membrane—are always open. They are like little holes in a bucket. Much as holes let water leak out of a bucket, these open channels let K⁺ leak out of a neuron. K⁺ diffuses out through these channels because of the K⁺ concentration gradient (a higher K⁺ concentration inside than outside).

This diffusion of K⁺ (positive charges) out of a neuron leaves behind unbalanced negative charges inside the neuron. These negative charges tend to pull K⁺ back into the cell because of the attraction of positive and negative charges. Remember that the charges we are discussing are positioned on the membrane surfaces. As K⁺ leaks out, positive K⁺ charges accumulate on the outer surface of the cell membrane. At the same time, unbalanced negative charges accumulate on the inner membrane surface. In this way, a voltage difference is created across the cell membrane.

In a resting neuron, K⁺ is freer to cross the membrane than other ions because the channels for other ions are mostly closed. As a useful approximation, we can assume that only K⁺ crosses. K⁺ ions diffuse out through K⁺ leak channels until the voltage difference—negative on the inside—pulls K⁺ back inside with exactly the same force as the concentration gradient drives K⁺ out. At this equilibrium point, K⁺ stops moving through the membrane. There is no further net movement of K⁺. The membrane potential in this equilibrium state is called the equilibrium potential of K⁺. Simply put, if K⁺ is the only ion that is free to diffuse across the cell membrane in a resting neuron, its diffusion drives the cell’s membrane potential toward the K⁺ equilibrium potential, which is the voltage difference that will draw K⁺ into the cell to the same degree as the high inside K⁺ concentration makes K⁺ diffuse out.

The Nernst equation predicts an ion’s equilibrium potential

Let’s now look at the general principles that are exemplified by K⁺ diffusion in a resting neuron. These are the principles of electrochemical equilibrium. The principles are easiest to understand when the channels for only one ion are open and, as a result, only one ion can diffuse across the membrane. When these conditions exist, we can say that the membrane is permeable to just the one ion.

Suppose the concentration of an ion is different on one side of a membrane than the other, and suppose also that one side is more positive than the other. In this case there will be two effects on ion diffusion. There will be a concentration effect on diffusion: the ion will tend to diffuse across the membrane from the side of high concentration to the side of low concentration. There will also be an electrical effect on diffusion: the ion will tend to diffuse across the membrane because of electrical attraction, moving toward the side where the charge on the cell membrane is opposite to the ion’s charge. As the ion diffuses across the membrane, its diffusion will modify both effects by changing the electric charge difference and concentration difference across the membrane.

Ion diffusion across the membrane will continue until the concentration effect and electrical effect become equal and opposite. This is the state of electrochemical equilibrium: a state in which the electrical effect causes diffusion in one direction and the concentration (chemical) effect causes diffusion of equal magnitude in the opposite direction. When an ion has reached electrochemical equilibrium, there is no net diffusion of the ion across the membrane in either direction:

In studies of neurons, the electric potential difference at electrochemical equilibrium is usually called the equilibrium potential of the ion and is symbolized E_ion. This potential can be calculated from the ion concentrations inside and outside the cell membrane by use of a famous equation called the Nernst equation.

In this equation, z is the number of charges per ion, T is the absolute temperature, R is a constant (the universal gas constant), and F is another constant (the Faraday constant).

The Nernst equation can be used whenever we can assume that only a single ion is able to diffuse across a membrane. In such cases, the equation predicts the equilibrium membrane potential. For example, we have already said that in a resting neuron, just one ion, K⁺, can readily cross the cell membrane because the open channels are mostly K⁺ channels. Under these circumstances, K⁺ is expected to diffuse to electrochemical equilibrium, and this diffusion is expected to determine the membrane potential. Taking account of the concentrations of K⁺ inside and outside the cell, the K⁺ equilibrium potential, E_K, calculated with the Nernst equation is about −85 mV, depending on temperature. The actual neuron resting potential, as we have said, is close to this, about −65 mV. The principal reason the equation’s prediction is a little off is that resting neurons are slightly permeable to other ions besides K⁺.

As we will see, the Nernst equation can be applied to any ion, not just K⁺, and helps explain each of the major phases of an action potential. It can be used, in an approximate way, to calculate the equilibrium membrane potential whenever just one ion accounts for most diffusion across the membrane and other ions are diffusing to just a minor extent.

Ion distributions across nerve cell membranes are not always at equilibrium. In fact, they sometimes are far from equilibrium. In such cases, ions will move toward equilibrium. The principles of electrochemical equilibrium are then useful for predicting the direction of ion diffusion.

Gated ion channels can alter the membrane potential

Instead of being open all the time like the K⁺ leak channels, most ion channels behave as if they contain gates: they are open under some conditions and closed under others. The channels for ions other than K⁺ are gated channels for the most part. And even most K⁺ channels are gated. Most gated channels are closed in a resting neuron, explaining why the K⁺ leak channels determine the resting membrane potential.

We categorize gated channels on the basis of the agent that causes them to open or close (FIGURE 34.5):

• Voltage-gated channels open or close in response to local changes in the membrane potential.
• Stretch-gated channels open or close in response to stretch or tension applied to the cell membrane.
• Ligand-gated channels have binding sites where they bind noncovalently with specific chemical compounds that control them. A compound that controls a channel is termed a ligand of that channel. A ligand-gated channel opens and closes depending on whether it is bound to its ligand. Although Figure 34.5C shows a ligand-binding site on the outside of the cell membrane, binding sites (e.g., for second messengers) can also be on the inside.

Figure 34.5: Three Types of Gated Ion Channels

Openings and closings of gated channels alter the membrane potential. For example, let’s consider what happens in a resting neuron if some of the Na⁺ channels in the cell membrane open (Na⁺ channels are ordinarily closed in a resting neuron). If Na⁺ channels open, Na⁺ ions diffuse into the neuron from the outside. This is true because Na⁺ is far from electrochemical equilibrium in a resting neuron. Na⁺ is far more concentrated outside the cell than inside, and this concentration difference tends to drive diffusion into the cell. The electrical difference also tends to drive Na⁺ diffusion into the cell because the cell membrane is negative on the inside in a resting neuron, attracting positive ions. The inward diffusion of Na⁺—caused by both concentration and electrical effects—represents an inward flow of positive charges which makes the inside of the neuron cell membrane become less negative. In other words, the voltage difference across the membrane (the membrane potential)—which is ordinarily near −65 mV in a resting neuron—becomes smaller. Perhaps it becomes −60 mV instead of −65 mV.

Depolarization is said to occur whenever the charge on the inside of a neuron cell membrane becomes less negative—relative to the charge on the outside—than it is at rest. In Concept 34.1 we implied that depolarization is either present or absent. Actually, varying degrees of depolarization can occur.

Hyperpolarization can also take place. It occurs whenever the charge on the inside becomes more negative. Opening and closing of gated ion channels can cause either depolarization or hyperpolarization, depending on which ions are affected.

Changes in membrane potential can be graded or all-or-none, depending on whether a threshold is crossed

Two types of changes in membrane potential occur: graded and all-or-none. The type of change that occurs depends on whether a voltage threshold of about −50 mV is crossed. We will start by discussing graded changes.

FIGURE 34.6A shows variations in membrane potential over time in a neuron in which the voltage threshold is not crossed. Note that the membrane potential can be high, low, or in between. These changes are described as graded because any value of the membrane potential is possible. The changes are caused by various gated ion channels opening or closing—some causing the membrane potential to shift in one direction, some causing it to shift in the other direction.

Figure 34.6: Graded and All-or-None Changes in Membrane Potential (A) Graded changes in membrane potential may not reach the voltage threshold. (B) When graded changes in membrane potential reach the voltage threshold, the membrane generates a large all-or-none change in membrane potential—the action potential.

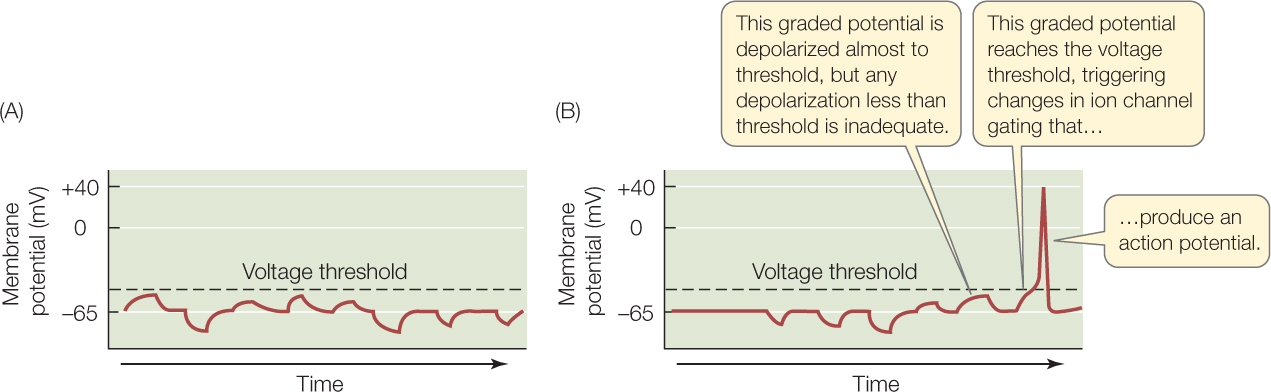
Graded changes of the membrane potential spread only a short distance from the locations of the ion channels that cause them. If a set of Na⁺ channels opens, for example, the change in membrane potential will be greatest at the location along the cell membrane where the channels are found. The change will spread on either side. But it will become smaller and smaller at greater and greater distances from the channels:

Let’s now discuss all-or none changes in the membrane potential. If a neuron depolarizes to the point that its inside charge is within about 50 mV of the outside charge, a massive, all-or-none event occurs: an impulse, or action potential, is triggered (FIGURE 34.6B). A membrane potential of about −50 mV is thus the voltage threshold for an action potential. An action potential is described as all-or-none because, when it occurs, it is always the same size. Action potentials are not graded. Moreover, as we’ll soon discuss, an action potential does not become smaller and smaller as it moves away from the location on a cell membrane where it originates. It stays the same in size as it propagates along the cell membrane of the axon of the neuron.

Graded changes give rise to all-or-none changes when the voltage threshold is crossed, and this interaction between the two types of changes provides one of the most important mechanisms by which a neuron carries out integration. Graded changes in membrane potential at a single location in the cell membrane add together. Suppose, for example, that a neuron simultaneously receives four signals—A, B, C, and D—that affect different types and numbers of gated ion channels in the neuron cell membrane, producing graded changes in the membrane potential. Suppose that at a particular spot on the cell membrane, signal A causes a 2.5-mV depolarization, B causes a 1.5-mV depolarization, C causes a 1-mV hyperpolarization, and D causes a 1-mV depolarization. All these graded changes in the membrane potential sum together. Thus at this particular spot, the membrane potential will be depolarized by 4 mV. It will be −61 mV instead of −65 mV as at rest.

The spot of greatest importance for this type of integration in a neuron is the axon hillock, where the axon arises from the cell body (see Figure 34.2). This is the spot where action potentials are most commonly initiated. A neuron may be receiving hundreds or thousands of signals at its dendrites and cell body. These signals bring about graded changes in membrane potential that spread to the axon hillock, where all the depolarizations and hyperpolarizations sum.

As this summation occurs, if the membrane potential at the axon hillock varies only in the range below about −50 mV, as in Figure 34.6A, no action potentials are produced. Moreover, no electric signals reach the axon terminals because the graded potentials disappear over the distance between the axon hillock and the axon terminals.

However, as the summation of graded potentials occurs, if the membrane potential at the axon hillock crosses the threshold as at the right in Figure 34.6B—that is, if it becomes −50 mV or even more depolarized—the axon hillock initiates an action potential. This action potential travels to the axon terminals, and the axon terminals then send signals to the other cells they innervate.

These processes are the major means by which a single neuron integrates its inputs to determine its outputs. In short, all the inputs create small, graded changes of membrane potential that sum together as they spread. If their integrated effect is a membrane potential that is not as depolarized as about −50 mV, the neuron produces no action potentials. But if their integrated effect is a membrane potential that is depolarized to at least −50 mV, the neuron generates one or more action potentials that propagate long distances down the axon.

An action potential is a large depolarization that propagates with no loss of size

An action potential, or nerve impulse, is a large, brief, localized change in the membrane potential—so large that the polarity reverses from inside-negative to inside-positive. During an action potential, the membrane depolarizes from −65 mV at rest to about +40 mV: a change of more than 100 mV. This event is extremely brief. It lasts only about 1 millisecond. It is also very localized: it is restricted to just a small region of the cell membrane.

An action potential propagates with no loss of size, however. Propagation occurs because an action potential at one location in the cell membrane of a neuron causes currents to flow that depolarize neighboring regions to the voltage threshold. When an action potential occurs in the axon hillock, currents flow into the neighboring region of the axon that is closer to the axon terminals, causing a graded depolarization there that is great enough that threshold is reached. That region then produces an action potential. Currents from that action potential then spread into the axon region still closer to the axon terminals. That region then produces an action potential. Each region of the axon stimulates the next region to produce an action potential until the action potential reaches the axon terminals. This process is what is meant by “propagation” in discussions of neuron function. Recall that action potentials are all-or-none and always the same size. Thus there is no loss of magnitude as an action potential propagates along the length of an axon.

Why does the cell membrane depolarize so profoundly during an action potential? And why does this depolarization end so quickly—within a millisecond? The properties of voltage-gated K⁺ and Na⁺ channels in the neuron cell membrane are chiefly responsible.

When the membrane potential in any local region of an axon reaches threshold, massive numbers of voltage-gated Na⁺ channels in that region quickly open. Suddenly, therefore, the principal ion that can cross the membrane becomes Na⁺, instead of K⁺. This results in a sudden, rapid influx of Na⁺ ions into that part of the axon because, as we discussed earlier, both the Na⁺ concentration difference and the electrical difference across the cell membrane favor inward Na⁺ diffusion. If Na⁺ were the only ion that could cross the membrane at this stage and if enough time were available to reach electrochemical equilibrium, the membrane potential would become E_Na—the equilibrium potential for Na⁺ (about +50 mV according to the Nernst equation). The membrane potential in fact almost reaches E_Na: it typically becomes about +40 mV (FIGURE 34.7, transition from A to B). Quickly, however, the Na⁺ channels close, and voltage-gated K⁺ channels, which respond in a delayed fashion to the local membrane potential, open in massive numbers. With the Na⁺ channels closed and the voltage-gated K⁺ channels open, the principal ion that can cross the membrane becomes K⁺. K⁺ diffuses out of the cell because K⁺ is more concentrated inside than outside and also because, at this moment (with the membrane potential at +40 mV), the outside of the cell membrane is relatively negative, attracting K⁺. The movement of K⁺ out of the cell drives the membrane potential back toward −65 mV, which is close to E_K, the K⁺ equilibrium potential (Figure 34.7C).

Figure 34.7: Production of an Action Potential The diagrams to the left show changes in voltage-gated Na⁺ and K⁺ channels, and those on the right show changes in membrane potential during (A) rest, (B) the rising phase of an action potential, and (C) the falling phase. The black rectangles on the membrane potential curves indicate the part of the curve during which the events diagrammed at left occur. The closing of the Na⁺ channels in (C) is of a specialized type (called inactivation) that cannot be reversed (i.e., the channels cannot reopen) for a brief period. K⁺ leak channels are always open.

Positive feedback (see Concept 29.6) plays a major role in the depolarization phase of an action potential (FIGURE 34.8). Positive feedback occurs because the Na⁺ channels are voltage-gated and the voltage across the neuron cell membrane is rapidly changing. When the cell membrane becomes partly depolarized, some voltage-gated Na⁺ channels open. Na⁺ ions then cross the cell membrane faster (diffusing from outside to inside) and depolarize the membrane even more. This greater depolarization causes more voltage-gated Na⁺ channels to open. This positive-feedback loop continues until all the voltage-gated Na⁺ channels open and maximum depolarization (approaching E_Na) occurs.

Figure 34.8: Positive Feedback Plays a Key Role in the Generation of an Action Potential During the rising phase of an action potential, positive feedback progressively drives all voltage-gated Na⁺ channels to open.

Why does an action potential travel in just one direction along an axon? After any particular local part of the axon membrane has produced an action potential, it undergoes a brief refractory period during which it cannot produce another action potential. Thus as an action propagates along an axon, the region of the cell membrane just behind it is in its refractory period. Currents are able to induce an action potential only in the neighboring region in the direction of the axon terminals.

Action potentials travel particularly fast in large axons and in myelinated axons

Action potentials do not travel along all axons at the same speed. Because of physical laws, they tend to travel faster in large-diameter than in small-diameter axons. This principle has been particularly important in the evolution of invertebrate nervous systems. Many invertebrates have evolved axons of large diameter that increase the speed of conduction of action potentials to muscles on which the animals depend for rapid escape from danger. In squid, for example, the muscle cells used for escape swimming are innervated by giant axons that in some cases are 1 millimeter in diameter. These giant axons are relatively easy to manipulate and study. Many of the basic principles of neuron function were discovered by studying them.

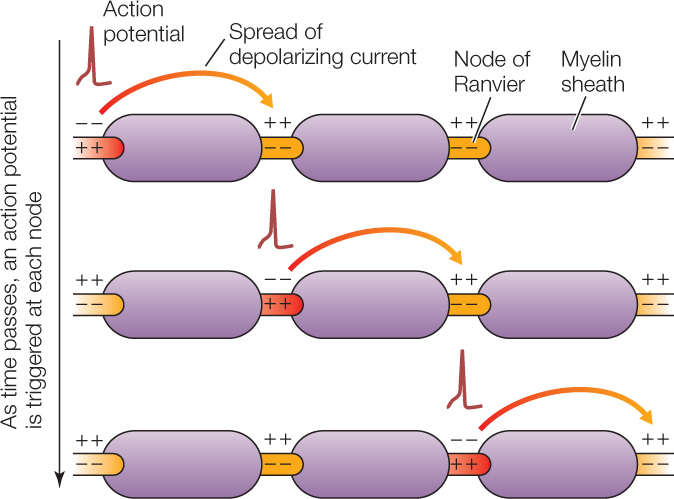
Vertebrates have evolved an additional means of increasing the speed of conduction: myelination. When glial cells wrap around axons, covering them with myelin, they leave uncovered spaces, called nodes of Ranvier, in between (see Figure 34.3). In a myelinated axon, action potentials are generated only at the nodes of Ranvier, because voltage-gated ion channels are clustered at these nodes and also because the myelin-covered axon segments are too well insulated electrically to permit rapid ion fluxes (flows) across the cell membrane. As an action potential travels along a myelinated axon, it jumps from one node of Ranvier to the next, a process called saltatory (“jumping”) conduction. For an axon of any particular diameter, an action potential travels far faster by saltatory conduction than it would by continuously traveling the entire length of the axon membrane:

Now that we have described how an action potential is generated and propagated along an axon, we will address the question of what happens when the action potential arrives at the axon terminal. How is the information communicated to the next cell?