Concept 42.2: Births Increase and Deaths Decrease Population Size
The size of anything, whether a bank account or a population, changes over time through additions and subtractions. Consider the size of something in the future. The size of your bank account, for example, will be equal to the amount of money you have now, plus the amount that is added, minus the amount that is taken out. What differs between bank balances and population sizes are the processes that add or subtract. In the case of your bank account, deposits and interest add to your balance, while withdrawals and bank fees subtract from it. In the case of populations, births (or the production of new individuals via seeds in the case of seed plants) add individuals, while deaths remove individuals. To spell this out,
the number of individuals in a population at some time in the future = the number now + the number that are born–the number that die
If we turn this word equation into symbols, we have the most basic mathematical model of population size:

where N is the population size, B is the number of births in the time interval from time t to time t + 1, and D is the number of deaths in that same interval. Ecologists call this equation the “birth–death” or BD model of population size.
We can use Equation 42.1 to understand population dynamics. Most often, the size of a population does not remain constant over time—the population grows or shrinks. Ecologists call the amount of change over a specific amount of time the growth rate of the population (a somewhat confusing term until we realize that when a population shrinks, its growth rate is negative). The population growth rate can be obtained from Equation 42.1 in two steps. First, we subtract Nt (the present population size) from both sides of the equation to obtain the change in population size:
Nt+1 − Nt = ΔN = (Nt − Nt) + B − D = B − D
The term ΔN is shorthand for the change in population size (using the convention that the Greek letter delta means “change in”). Next, we divide both sides by ΔT, the time interval from t to t + 1, to obtain the change per unit of time:
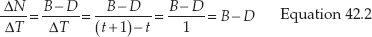
This shows, logically enough, that the change in size over one time interval is the number of births minus the number of deaths during that interval.
Change in the size of a population can be measured directly only for very small, countable populations, such as a zoo population. Ecologists can get around this difficulty by keeping track of a sample of individuals over time. From this sample, they can estimate the number of offspring that the average individual produces, called the per capita birth rate (b), and the average individual’s chance of dying, called the per capita death rate (d), in some interval of time. Per capita (literally, “per head”) means “per individual.” Total birth and death rates in the population can then be estimated by multiplying per capita birth and death rates by population size, so that B = bNt and D = dNt. Substituting into Equation 42.1, we have
867
APPLY THE CONCEPT: Births increase and deaths decrease population size
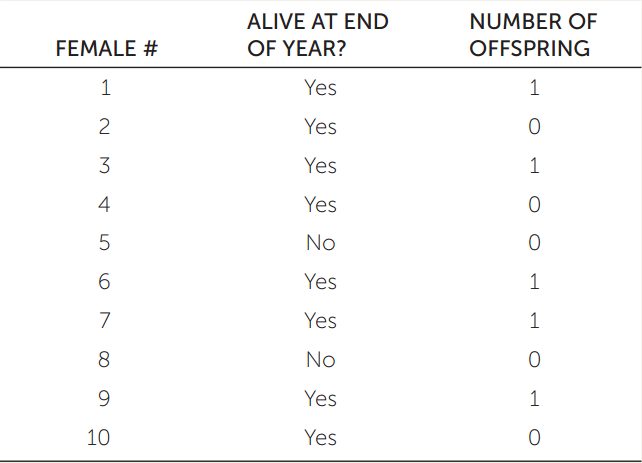
Jane is a rancher who is considering shifting her operation from cattle to American bison (Bison bison), to take advantage of the demand for lean, healthy bison meat. To decide, she needs to know how well bison will do on her ranch. She buys 50 female bison that are already inseminated and places 10 of them, picked at random, into their own pasture. These 10 females serve as a sample from which Jane collects demographic data over one year. Use her data to answer the questions below.
- How many total births and how many total deaths occurred in this sample population?
- What were the estimated average per capita birth and death rates (b and d) for the entire bison herd, based on this sample?
- What was the estimated per capita growth rate (r)?
- Based on these estimates, what was the size of Jane’s entire bison herd at the end of the year? (Hint: Use Equation 42.3.)
Nt+1 = Nt + bNt − dNt
or equivalently,
Nt+1 = Nt + (b − d)Nt
The value (b − d)—the difference between per capita birth rate and per capita death rate—represents the average individual’s contribution to total population growth rate. This value is the per capita growth rate, which ecologists symbolize as r. Substituting r for (b − d), we have

By converting Equation 42.3 into an equation of growth rate analogous to Equation 42.2, we get

What happens if per capita birth rate is greater than per capita death rate, or if death rate is greater than birth rate, or if they are equal? If b > d, then r > 0, and the population grows. If b < d, then r < 0, and the population shrinks. If b = d, then r = 0, and the population size does not change.
We are now in a better position to understand why population sizes or densities change over time: they have to unless the number of births exactly equals the number of deaths. We are also in a better position to understand why population densities vary in space. We saw in Chapter 41 that barriers to dispersal can cause species to be absent from some places. Another possible reason for a species’ absence from a place is a negative population growth rate. A species will not persist in a given location if its per capita growth rate, r, is negative there. Any population that decreases steadily in size over time eventually reaches a density of zero—that is, it goes extinct.
CHECKpoint CONCEPT 42.2
- What is the relationship between per capita birth rate and the total number of births in a population during a time period?
- What do we need in addition to estimates of per capita birth and death rates in order to predict population size at some future time?
- What two strategies could Jane the rancher (see Apply the Concept on this page) use to expand her bison herd faster?
We can understand the dynamics of whole populations, and even some aspects of spatial variation in abundance, if we can estimate the average birth and death rates of the individuals that constitute those populations. What determines these variables?