Concept 42.5: Immigration and Emigration Affect Population Dynamics
Many species occupy habitat patches that are separated from other patches by unsuitable environments (FIGURE 42.10; see also Figure 42.1). Each patch of suitable habitat occupied by the species can be thought of as a subpopulation, and the set of subpopulations in a region is known as a metapopulation. When subpopulations are not too isolated from one another, individuals occasionally move, or disperse, among them.

When dispersal is possible, each subpopulation changes as all populations do—through births and deaths—but with the added input of individuals that move into the subpopulation (immigrants) and loss of individuals that move away (emigrants). Adding the number of immigrants (I) and emigrants (E) to the BD growth model, we get the BIDE model:
The number of individuals in a population at some time in the future = the number now + the number that are born + the number that immigrate − the number that die − the number that emigrate
In the BD model, populations are considered closed systems because there is no immigration or emigration—no individuals move into or out of them. In the BIDE model, subpopulations are considered open systems because individuals can move among them. This difference has a profound effect on population dynamics. In the BD model, a subpopulation that goes extinct stays extinct: once the subpopulation reaches zero, there are no individuals left to reproduce. With the BIDE model, however, immigration can bring an extinct subpopulation “back to life.”
You may think that extinction is rare, but in fact it is fairly common in small habitat patches, even when the environment of the patch is favorable. When subpopulations are small, there is a reasonable possibility during any time period that by chance no female will give birth and that all adult individuals will die—in which case the subpopulation will be extinct. Small populations are also more likely than large ones to go extinct following environmental disturbances.
877

Go to ANIMATED TUTORIAL 42.3 Metapopulation Simulation
PoL2e.com/at42.3
Once a subpopulation goes extinct, it will remain at zero density—and its patch of habitat will remain unoccupied—unless individuals move into, and thus recolonize, the patch. Thus if there is no dispersal among patches, the subpopulations will “wink off” one by one. The time to extinction of the entire metapopulation is longer the larger each subpopulation is, and the more subpopulations there are, but extinction will occur nonetheless. If subpopulations are connected by dispersal, however, the metapopulation as a whole will persist much longer, for two reasons. First, immigration can repopulate unoccupied patches, and “rescue” declining subpopulations from extinction. The repopulated patches, in turn, can colonize others, causing them to “wink on.” Second, immigrants contribute to the genetic diversity within subpopulations by bringing new alleles with them. This gene flow combats the erosion of genetic diversity through genetic drift that can reduce r and compromise a species’ evolutionary potential.
LINK
Gene flow and genetic drift are discussed in Concept 15.2
We can see the recolonization process at work in the metapopulation of Edith’s checkerspot butterfly in the San Francisco Bay area (see Figure 42.1). Many subpopulations of this endangered butterfly went extinct during a severe drought that gripped California between 1975 and 1977. The only subpopulation that did not go extinct was the largest one, on Morgan Hill. The extinct subpopulations remained at zero density until 1986, when nine suitable habitat patches were recolonized from the Morgan Hill source population. Patches closest to Morgan Hill were most likely to be recolonized because adult butterflies do not fly very far.
APPLY THE CONCEPT: Immigration and emigration affect population dynamics
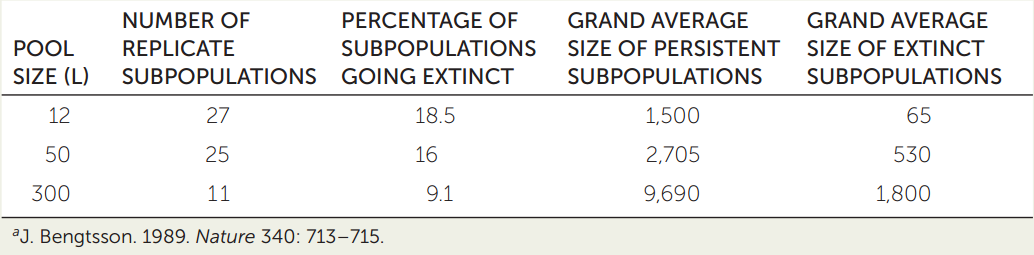
In a study of subpopulations of Daphnia in Swedish rock pools (see Figure 42.10), ecologist Jan Bengtsson established a number of artificial rock pools that held either 12, 50, or 300 liters of water. He introduced the same number of Daphnia to each pool and then covered the pools with mesh, which prevented immigration or emigration. Over the next 4 years, Bengtsson returned repeatedly to count the Daphnia, thereby obtaining the average size of the subpopulation in each pool. If a subpopulation went extinct, he included only the nonzero values for the size of that subpopulation measured before extinction in calculating its average size. The table shows the grand average of these time-based averages for pools in which the subpopulations went extinct, and for those in which they persisted. Use the table to explore how extinction risk changed with the volume of a pool and the number of Daphnia in it.a
- Graph the relationship between pool size and percentage of subpopulations that went extinct, using size as the x axis. What does your graph show you?
- Within each pool size, which subpopulations were at greatest risk of extinction?
- How are these two results related to each other?
- What might have happened if Bengtsson had not placed mesh over his experimental pools?
878
CHECKpoint CONCEPT 42.5
- What is the fundamental difference between the BD (see Concept 42.2) and BIDE models of population growth?
- Barriers to dispersal and environmental tolerance both influence where a species is found. Which of these factors is more important in determining the geographic range of a species, and which is more important in determining which habitats a species occupies within that geographic range?
- Human-caused changes in land use often break up the original habitat of a species into spatially separated fragments. Why is this likely to increase the risk of extinction?
In Chapter 41 we saw that ecological knowledge has many important applications in our everyday lives—in medicine, agriculture, and other areas. Our understanding of the dynamics of populations and metapopulations provides tools that allow us to influence their fates, as several examples will illustrate.