Chapter 1. Mirror Experiment Activity 13.1
Mirror Experiment Activity 13.1
The experiment described below explored the same concepts as the one described in Figure 13.1 in the textbook. Read the description of the experiment and answer the questions below the description to practice interpreting data and understanding experimental design.
Mirror Experiment activities practice skills described in the brief Experiment and Data Analysis Primers, which can be found by clicking on the “Resources” button on the upper right of your LaunchPad homepage. Certain questions in this activity draw on concepts described in the Statistics primer. Click on the “Key Terms” buttons to see definitions of terms used in the question, and click on the “Primer Section” button to pull up a relevant section from the primer.
Experiment
Background
As you have learned, researchers are able to sequence an organism’s genome by digesting or breaking it apart into smaller pieces, sequencing the resulting small genomic fragments, and then aligning these fragments based on sequence overlaps. Although it can be remarkably informative to look at the whole genome sequence of a single organism, researchers can also gain a great deal of information when they compare the whole genome sequences of two different species. They can identify mutations in the genetic sequences that are unique to one species or the other, and can isolate mutations that might be responsible for the different phenotypes observed in these organisms. How different are the sequences of the human and chimpanzee genomes? And if any differences exist between the whole genome sequences of humans and chimpanzees, can these differences help us understand how our species evolved?
Hypothesis
The Chimpanzee Sequencing and Analysis Consortium (CSAC) – a group of over 60 researchers at different institutions – hypothesized that by comparing the whole genome sequences of humans and chimpanzees, mutations that were unique to humans or to chimpanzees could be identified. They could effectively determine how different the chimpanzee and human genomes were from one another.
Experiment
Researchers isolated genetic material from the white blood cells of a chimpanzee. Using an approach similar to that outlined in Fig. 13.1, scientists constructed a preliminary whole genome sequence for this great ape. They compared the chimpanzee and human genomes, and counted the number of nucleotides that differed between these two sequences (Figure 1).
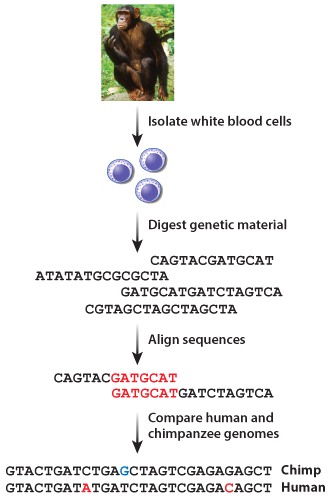
Photo credit: Anup Shah/Animals Animals-Earth Scenes
Results
As you will learn in later chapters, various types of mutations can occur in DNA sequences. Some of these mutations are a change in a single nucleotide, and are referred to as point mutations. Other mutations can involve larger chromosomal segments. A portion of a chromosome can be deleted and effectively removed from an organism’s genome. Chromosome segments can also be duplicated, resulting in extra material within the genome. Often, chromosomal mutations can affect thousands of nucleotides at a time.
The CSAC determined that, as a result of the combined action of point mutations and chromosomal insertions and deletions, the human and chimpanzee genomes differ in sequence by approximately 4%. Some of these differences between the human and chimpanzee genomes can be attributed to normal allelic differences between individuals in the same species. However, 1-2% of these differences are actually lineage-specific, meaning that they are not the result of normal variation within species, but true sequence differences that are unique to either the chimpanzee or human. Researchers were also able to identify certain chromosomal regions where mutations were more likely to occur, predict the rate at which certain genes diverged or evolved, and isolate a handful of mutations that could contribute to distinct human and chimpanzee phenotypes.
Source
The Chimpanzee Sequencing and Analysis Consortium. 2005. Initial sequence of the chimpanzee genome and comparison with the human genome. Nature. 437, 69-87.
Question
As you learned in Fig. 13.1, to sequence a whole genome, researchers will typically break the genome into small fragments, sequence them, and then reassemble these fragments based on sequence overlaps. Two small genomic fragments that have overlapping sequences form a structure known as a contig. The CSAC relied on contigs to sequence the chimpanzee genome.
If researchers isolated the above genomic fragments from chimpanzees, which sequences would constitute a contig?
| A. |
| B. |
| C. |
| D. |
| E. |