Chapter 1. Mirror Experiment Activity 5.8
Mirror Experiment Activity 5.8
The experiment described below explored the same concepts as the one described in Figure 5.8 in the textbook. Read the description of the experiment and answer the questions below the description to practice interpreting data and understanding experimental design.
Mirror Experiment activities practice skills described in the brief Experiment and Data Analysis Primers, which can be found by clicking on the “Resources” button on the upper right of your LaunchPad homepage. Certain questions in this activity draw on concepts described in the Experimental Design primer. Click on the “Key Terms” buttons to see definitions of terms used in the question, and click on the “Primer Section” button to pull up a relevant section from the primer.
Experiment
Background
During the mid-1900s, biologists debated the nature of the cell plasma membrane. Was it a “fluid” structure, whose components could move freely? Or were the lipids and proteins within the plasma membrane firmly anchored and relatively immobile? The advent of antibody staining techniques provided researchers with a new tool to track the movement of proteins and lipids within cell membranes. Specific proteins or molecules could now be tagged with fluorescent markers and subsequently visualized. This technique could be used to help determine the true nature of the plasma membrane.
Hypothesis
Cells derived from different species express unique surface antigens, or molecules located on the cell surface. These surface molecules associate with lipids or proteins within the plasma membrane. If a mouse cell and a human cell could be successfully fused and cultured, the expression of species-specific surface antigens could be assessed.
Investigators could then evaluate which of two alternative hypotheses is correct. If the cell membrane were a fluid structure, then proteins and lipids from both species would mix within the membrane, forming a “mosaic” structure of interspersed mouse and human surface antigens. If the cell membrane were rigid, then the membrane on one side of the cell would contain only mouse-specific surface antigens, and the membrane on the other side of the cell would contain only human-specific surface antigens.
Experiment
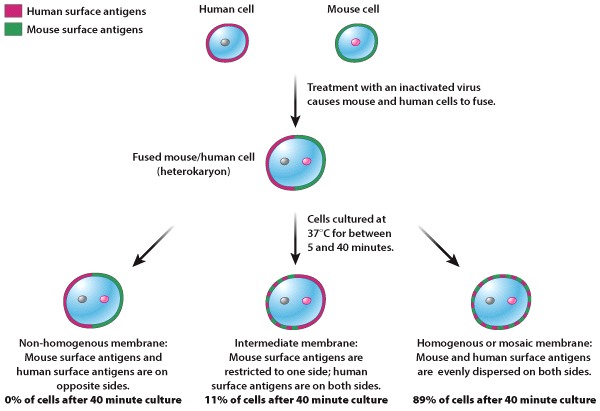
In the 1960s, L. D. Frye and M. Edidin successfully fused mouse and human cells, forming heterokaryotic cells that contained two distinct nuclei - one mouse and one human - and a mixture of mouse and human cytoplasm. These cells were cultured for between 5 and 40 minutes and subsequently stained for mouse and human surface antigens. Fused mouse/human heterokaryotic cells were placed into three different categories based on the distribution of mouse and human antigens within the plasma membrane (Figure 1):
- non-homogenous membranes: mouse surface antigens are on one side of the cell and human surface antigens are on the other side.
- intermediate membranes: either mouse or human surface antigens are restricted to one side of the cell, while the other antigen type is dispersed on both sides.
- homogenous or “mosaic” membranes: both mouse and human cell surface antigens are evenly dispersed on both sides of the cell.
Results
After 40 minutes in culture, most heterokaryotic cells had “mosaic” membranes, containing a homogenous distribution of mouse and human surface antigens. The plasma membrane thus appeared to be a fluid structure, in which proteins and lipids could move.
Source
Frye, L. D., Edidin, M., 1970. “The rapid intermixing of cell surface antigens after formation of mouse-human heterokaryons.” J Cell Sci. 7: 319–35.
Question
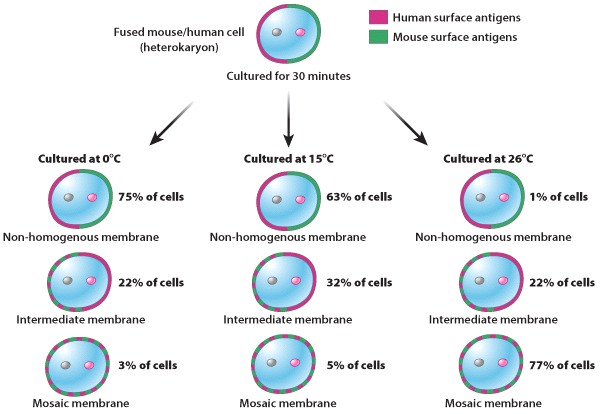
During the course of their experiments, Frye and Edidin cultured heterokaryotic mouse/human cells at different temperatures. They observed the results shown in Figure 2, below. What conclusions could they have drawn from this data?
| A. |
| B. |
| C. |
| D. |
| E. |