Chapter 1. Water Movement

Introduction

Water is the medium of life. All metabolically active cells are mostly water, and the biochemical processes needed to sustain life require that cells maintain their water content within a narrow limit.

This primer explores the movement of water into and out of cells with the goal of providing a quantitative and physical understanding of the underlying processes. We begin with a review of diffusion, and then move on to the important topic of osmosis. Our goal is to explain how a difference in solute concentration across a selectively permeable membrane can lead to a net movement of water. Osmosis then provides a basis for discussing osmotic pressure and turgor pressure. We conclude with a brief introduction to water potential, which is a means for combining all of the processes that affect water movement. Water potential can be used to describe water movement in all organisms, but is especially useful in understanding water transport in plants.

Diffusion

In Chapter 5, we learned that diffusion is the random motion of molecules and that differences in concentration lead to the net movement of molecules (or atoms) from regions of higher to lower concentration. To develop an intuitive understanding of diffusion and its role in biological systems, let’s look at how diffusion occurs at the molecular level.

Imagine a glass of water sitting on your desk. From your macroscopic viewpoint, the liquid appears motionless. But at the molecular level, the water is in constant motion. Individual molecules move rapidly (~ 500 meters per second) and collide with great frequency (~5 trillion (10¹²) collisions per second). The outcome of each collision is that the individual molecules move apart in a new direction. As a result of all these collisions and changes of direction, we can think of each molecule as following its own random “walk.”

Here is the key question for understanding diffusion: If the motion of individual molecules is truly random, how can it lead to a predictable behavior, specifically the net transport of substances from regions of higher to lower concentration?

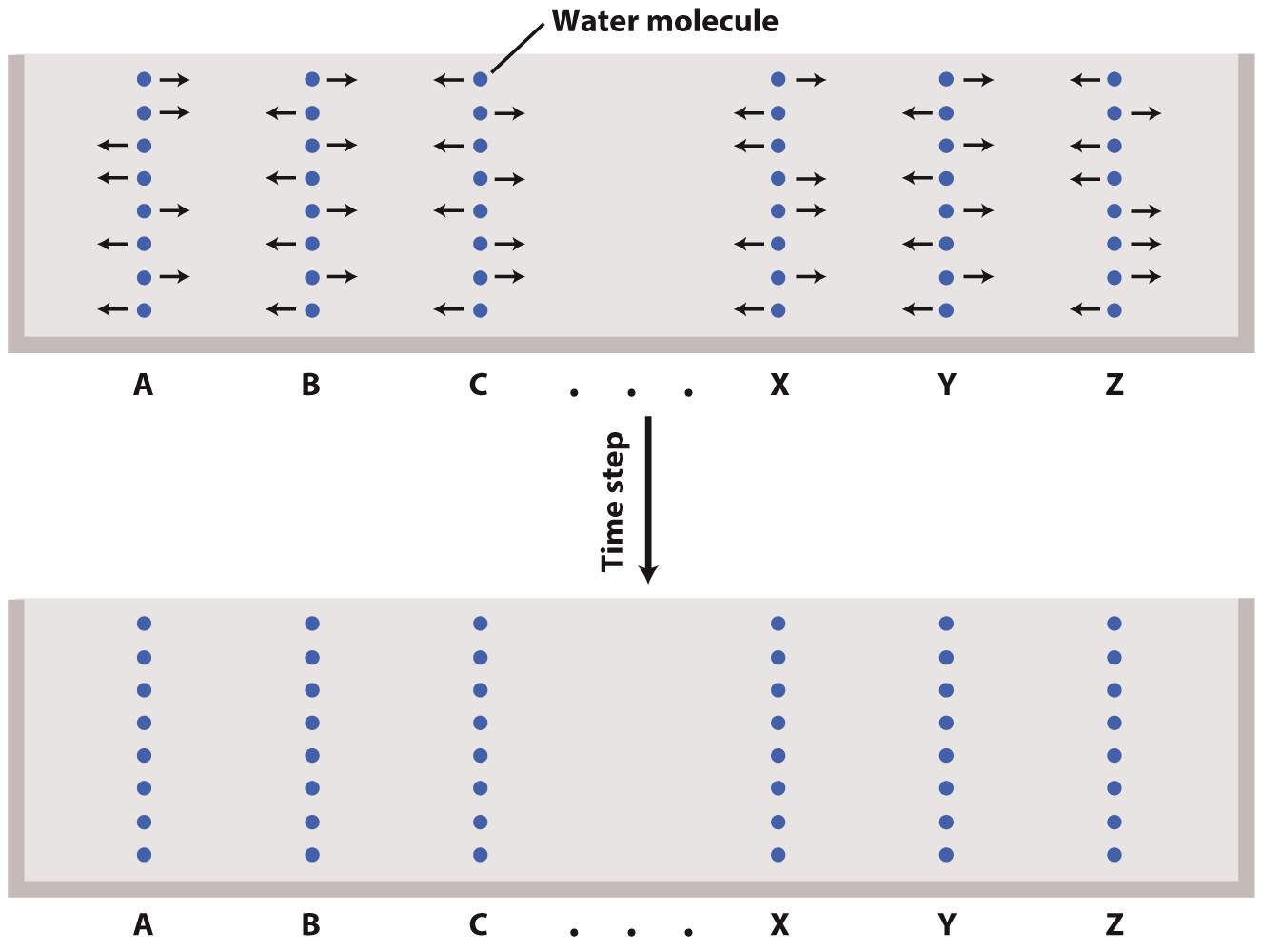
Consider the case in which molecules can move only along a straight line, that is, to the left or to the right. Imagine points along the line labeled from left to right by the letters of the alphabet. The points along the line are occupied by large numbers of particles, which move at a rate of one “step” (for example, from A to B) per time step. Our particles move at random, meaning that each has an equal chance of moving either one step to the right or one step to the left, but move they must! They cannot remain where they are – that is what it means for all particles to be in motion.

If we have even a moderate number of particles, then in one time step about half the particles at B will move to C, and the other half of the particles originally at B will move to A. Of course, about half the particles originally at A move to B, and about half of those originally at C move to B as well. As a result, if we start with all our particles evenly distributed across all the points on the line, they will remain more or less evenly distributed. We say more or less because, as the movement of each individual particle is random, rarely will exactly half the particles move left, and half move right, and so the local abundance of particles at any point in any time step tends to deviate from the long-term average; such variations are often described as "thermal fluctuations."

What happens if our particles are not initially evenly distributed? Suppose the initial number of particles is highest at A and decreases with each step to the right (B, C, etc.). Again, during a time step about half the particles at each location move to the right, and about half to the left. But because the initial distribution of particles is unequal, any location will tend to receive more particles from its neighbor to the left than it sends to the left, and fewer particles from its neighbor to the right than it sends to the right.

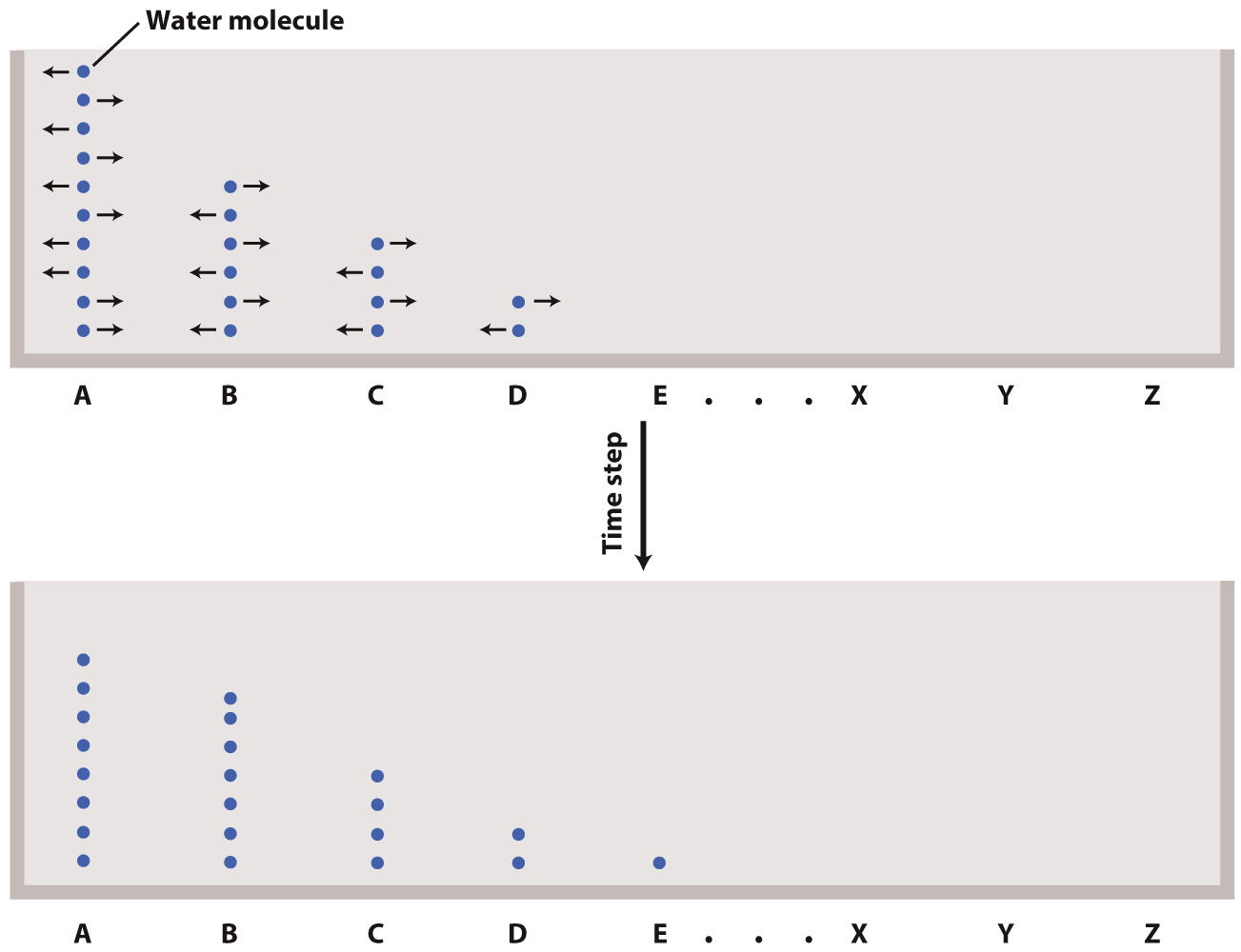
Thus, we observe a net movement of particles from regions of high concentration to low concentration (that is, left to right) that we call diffusive transport. Over a long enough period of time, diffusive transport results in an even (but still thermally fluctuating) distribution of particles, from which all information about the initial distribution has been lost.

What constitutes a long enough time for diffusion to act? For example, if signaling molecules are released from a point source, we might ask how long, on average, before they spread out enough to come into contact with a receptor located at a distance L from the source? If you walk directly a distance L at a constant speed, your transport time will scale linearly with L (time = distance/speed). In diffusive transport, recall that each molecule is on its own random walk, such that in any time step an individual molecule is equally likely to move toward the receptor as it is to move away from the receptor. The mathematical result of this random motion is that the time for diffusive transport scales not with length but with length squared (L²).

As a result, diffusion is fast over short distances, but becomes incredibly slow at even moderate distances. The average time for a glucose molecule to diffuse across a 10-µm cell is only 1 second and to diffuse across a 100-µm cell is 10 seconds. But to diffuse 1 mm would take, on average, 16 minutes, while to diffuse 1 m would take almost 32 years!

This means that only unicellular organisms can rely on diffusion alone. As discussed in Chapter 28, larger organisms circumvented the size limits imposed by diffusion by evolving vascular transport systems that distribute materials by bulk flow instead of diffusion.

Osmosis

Osmosis is the movement of water across a selectively permeable (semipermeable) membrane in response to a difference in solute concentration. When there is a difference in the concentration of solutes on two sides of a selectively permeable membrane, water will move across the membrane from the side with a lower concentration of solutes toward the side with a larger concentration of solutes.

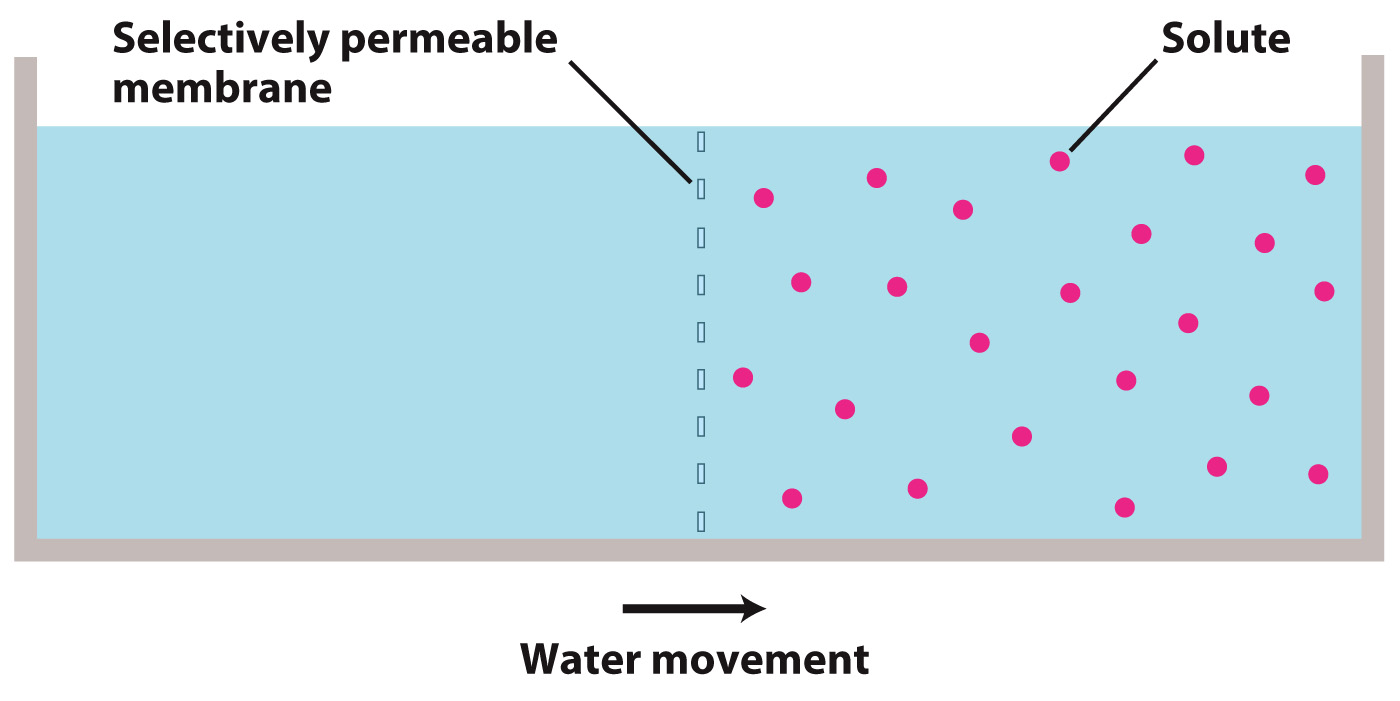
Osmosis can seem mysterious because the solutes on one side of the membrane appear to influence the movement of water on the other side of the membrane and thus to exert some sort of a force at a distance. As we will see, what drives osmosis is the effect of the solutes on the random movement of water molecules on the same side of the membrane.

Let's start by imagining a container of pure water. In this container, the randomly moving water molecules are equally likely to move from the left side of the container to the right side as they are from the right to the left.

Now we place a selectively permeable membrane across the center of the container. A selectively permeable membrane allows water to pass, but prevents solutes from passing. The membrane will also slow the movement of water molecules. Some water molecules bounce off the membrane, while others pass through it. However, as this bouncing off and passing through happen to the same extent on both sides of the membrane, the diffusion of water molecules from the left side to the right side and from the right side to the left side remains equal.

Next we add some solutes to the compartment on the left side of the membrane. The rate at which water molecules diffuse from the right side to the left side remains unchanged. But on the left side, as the solute molecules bounce off the selectively permeable membrane they collide with water molecules and in this way "frustrate" or slow the movement of water molecules toward the membrane. As a result, the net movement of water molecules will be from the right side (which has no solutes) to the left side (where the solutes are present).

If we increase the concentration of solutes on the left side, the larger number of solute molecules bouncing off the membrane makes it even harder for water molecules to reach the membrane. Thus, the net result of a higher solute concentration is to increase the rate at which water moves from the right side (no solutes) to the left side (solutes present).

Note that osmosis occurs even if there are solutes on both sides of a selectively permeable membrane. The net movement of water will be from the side that has a lower concentration of solutes toward the side that has a higher concentration of solutes.

Note also that (at least to a first approximation) the identity of the solute molecules does not matter. All molecules that do not pass through the membrane are equally effective in slowing the movement of water molecules toward the selectively permeable membrane.

Osmotic Pressure

We can prevent osmosis by applying a force to the compartment with the higher solute concentration. The externally applied force imparts to each molecule a greater tendency to move toward the membrane (that is, from higher to lower pressure) and thus increases the rate at which water molecules move out of the compartment with higher solute concentration.

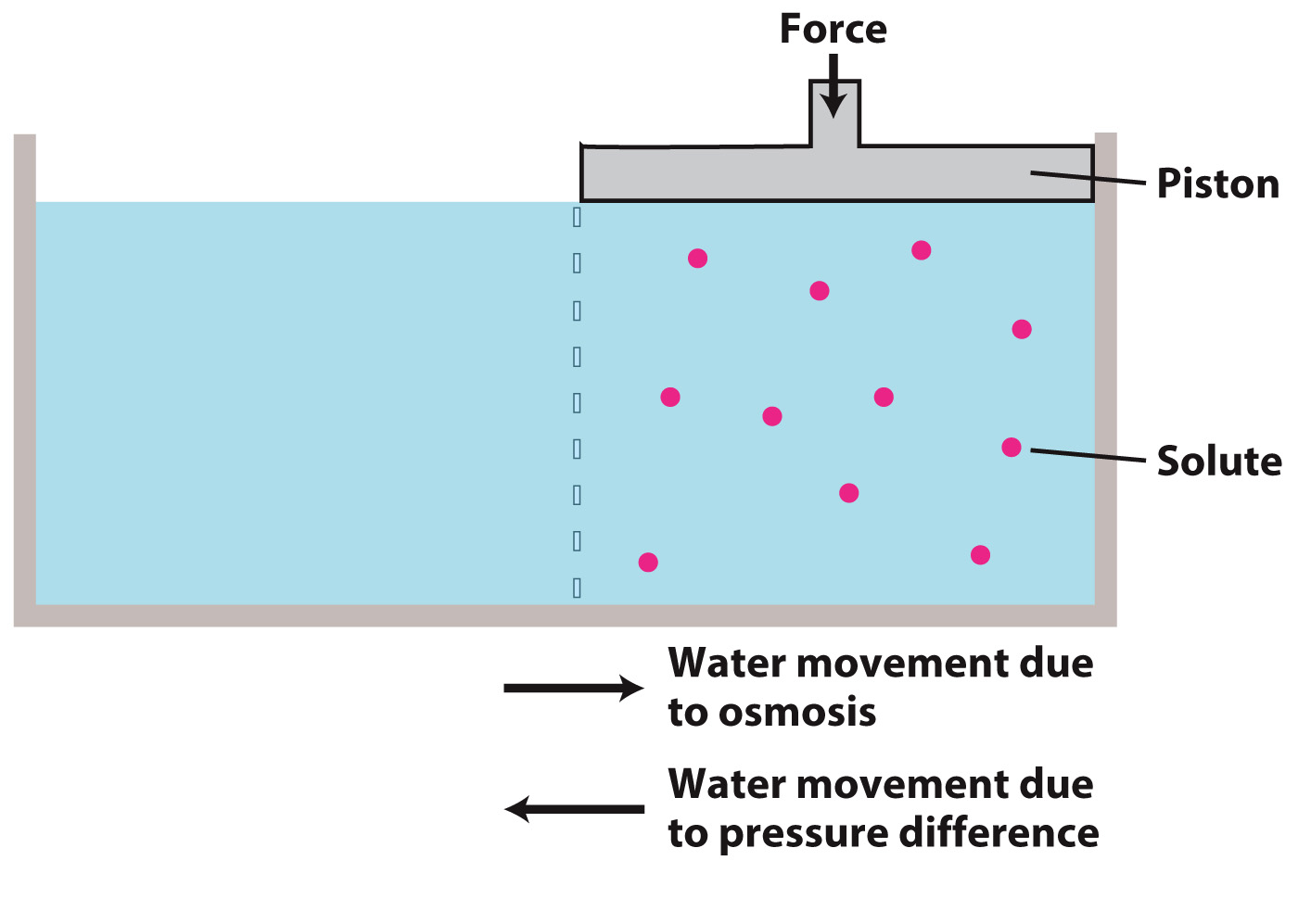
If we know the concentration of the solution, we can calculate the pressure needed to stop osmosis as RTC_s, where R is the gas constant (8.31 J/mol K), T is the temperature (K), and C_s is the solute concentration (mol/m³). Note that this equation assumes that solute molecules do not interact in any way and thus is strictly correct only for dilute solutions.

The pressure that would need to be applied to stop water from moving into a solution by osmosis is referred to as the "osmotic pressure." However, it is important to remember that osmotic pressure is not a real pressure that can be measured, but rather a way of describing the tendency of a solution to “draw water in” by osmosis.

Turgor Pressure

In contrast to osmotic pressure, turgor pressure is an actual pressure that develops as a result of water moving by osmosis into cells surrounded by a cell wall. Cells contain high concentrations of solutes (on the order of 500 to 1000 mol/m³). When in contact with sources of "fresh water" (total solute concentration < 30 mol/m³ (=0.03 mol/L)), a cell will swell as water moves into the cell by osmosis.

Turgor pressure develops because the cell walls resist being stretched and push back on the cell interior, just as a balloon pushes back on the air inside it. Water will continue to enter the cell until the turgor pressure increases to a level sufficient to stop osmosis.

Many organisms have cell walls: bacteria, fungi, many protists, most algae, and all plants. When these organisms live in terrestrial or freshwater environments (where solute concentrations are low), high turgor pressures are the norm. Changes in turgor pressure can play important physiological roles: for example, in the opening and closing of stomata in leaves or the transport of carbohydrates in the phloem (Chapter 29).

A cell without a cell wall will swell until it ruptures when exposed to fresh water. Some protists that live in freshwater habitats do not have cell walls, such as amoebas and paramecium. Instead, they have contractile vacuoles that actively expel the water that continually enters the cell by osmosis.

Water Potential

We have discussed how the presence of solutes can lead to the movement of water across a selectively permeable membrane, and we know from our daily life that pressure can cause water to move (water gushing from a garden hose), as can gravity (a stream flowing down hill). In large organisms such as trees, pressure, osmosis, and gravity all come into play.

Water potential – abbreviated as Ψ (psi) and having units of pressure – is a parameter that combines all three of the factors that influence the movement of water:

Ψ = Ψ_p + Ψ_s + Ψ_g

where these components refer to the effect of pressure ( Ψ_p), solutes ( Ψ_s), and gravity ( Ψ_g) on the movement of water. In a thermodynamic framework, Ψ is a measure of the "free energy" of water (joules per cubic meter) and thus of its capacity to do work. Water moves from higher to lower water potential, in the same way that water flows downhill.

To add together the effects of pressure, solutes, and gravity, we need to make sure that each is expressed on the same scale. The easiest way to do this is to describe each component in relation to a common reference state: typically the water potential of pure water (with no solutes) at atmospheric pressure and located at a reference elevation, for example, ground level. We designate this reference state as having a Ψ = 0. We can then write expressions for:

The pressure potential: Ψ_p = P, where P is the pressure of the water measured relative to atmospheric pressure.

The solute potential: Ψs = -RTC_s, where the negative sign reflects the fact that when solute concentration C_s ≠ 0, water flow, by osmosis, will be from the reference volume to the sample volume. Because water flows from higher to lower Ψ, the value of Ψ_s must be < 0 because the Ψ_s of our reference state = 0. The more concentrated a solution is, the lower (more negative) is its solute potential.

The gravitational potential: Ψ_g = ρgh, where ρ is the density of water (units: 1000 kg/m³), g is the acceleration due to gravity (9.81 m/s²), and h is the height above the reference elevation. If the reference elevation is the base of a tree, Ψ_g increases the higher we go in the tree.

Note that the units are in megapascals (MPa). The pascal is the SI unit of pressure. The weight of our atmosphere at sea level is 100,000 Pa (= 0.1 MPa); a properly inflated car tire is approximately 0.2 MPa.

What Causes Water to Flow Up a Tall Tree?

Water, important for all organisms, plays a key role in vascular plants. Water evaporates as the leaves open their stomata to obtain CO₂ needed for photosynthesis. Vascular plants must extract water from the soil and transport it to their leaves to replace the water lost through evaporation (Chapter 29).

Let's consider a tree at night and during the day.

At night, the stomata are closed and there is no movement of water through the stem. During the day, the stomata are open and water flows from the soil to the leaves to replace water lost by transpiration.

At night, because there is no movement of water (and no physical barriers to water flow from the soil to the leaves), the water potential must be the same at every point from the soil to the leaves:

Ψ_soil = Ψ_{root cell} = Ψ_{root xylem} = Ψ_{leaf xylem} = Ψ_{leaf cell}

When stomata are open during the day and water flows through the tree, the water potential in the leaves must be less than that of the soil since water moves from regions of higher to lower potential:

Ψ_soil > Ψ_{root cell} > Ψ_{root xylem} > Ψ_{leaf xylem} > Ψ_{leaf cell}

Note that here water is assumed to flow from the soil to the root cells, and from there into the xylem. Water exits the xylem in the leaf, flowing first into the leaf cells and then evaporating from the leaf during transpiration.

Let’s now look at the components of water potential in a 10-m-tall tree, considering first the situation during the night when stomata are closed. In our example, the soil is assumed to be fully wet and thus has a Ψ = 0. (Note: as soils dry, Ψ_soil becomes increasingly negative.)

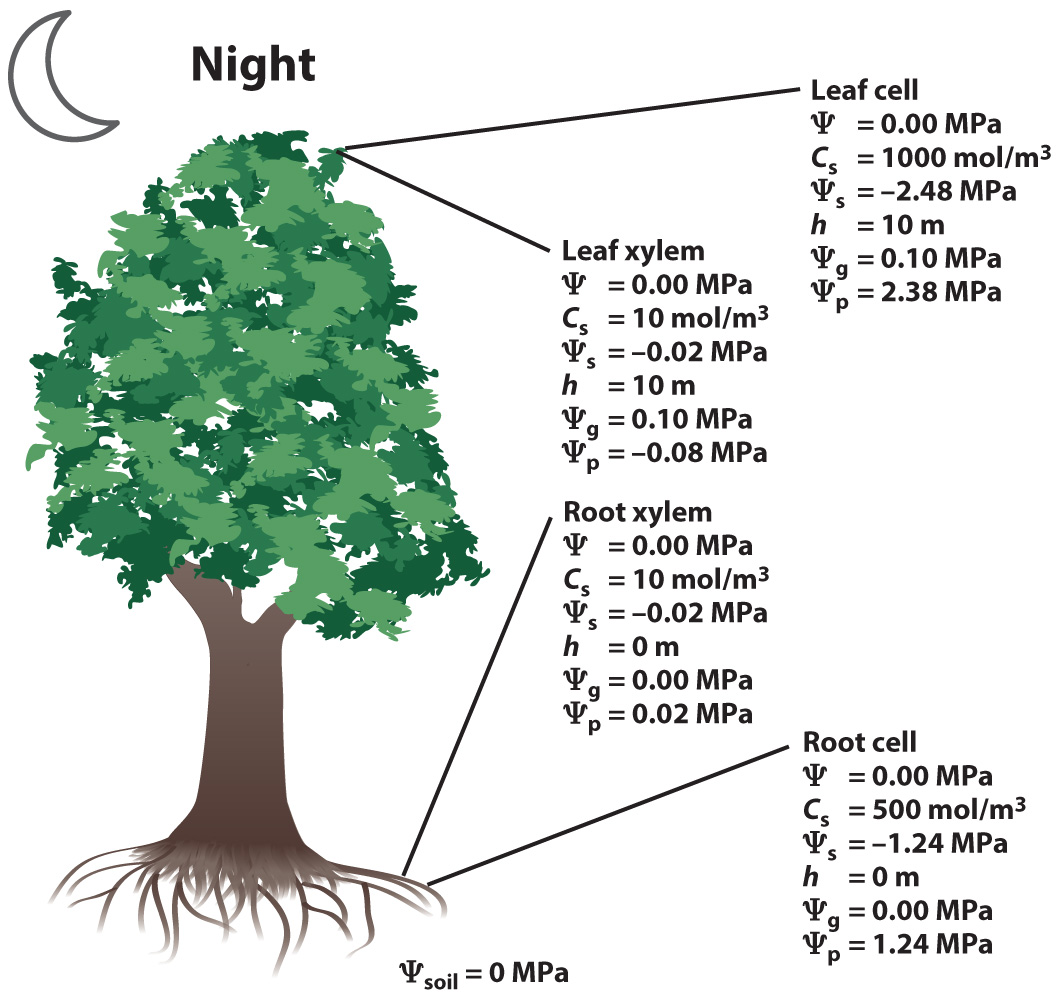
At night, Ψ is the same everywhere in our tree and thus the effects of pressure (Ψ_p), solutes (Ψ_s), and gravity (Ψ_g) must balance one another.

For example, in the living cells, we see that at the bottom (root) and top (leaf) of the tree the effect of solutes is to draw water in by osmosis (Ψ_s < 0), and this negative solute pressure is balanced by a positive turgor pressure (Ψ_p > 0). The Ψ_p in leaf cells is higher than in root cells, primarily because the concentration of solutes (C_s) is higher in the leaf cells; Ψ_g makes only a small contribution.

In the xylem, the concentration of solutes is low and thus Ψ_s makes only a small contribution to the overall Ψ. The major factors are the effect of gravity (Ψ_g higher at the top of the tree), which is balanced by a reverse gradient in Ψ_p. At the base of the tree, Ψ_p > 0 because the xylem walls resist stretching and push back on the water. The positive Ψ_p serves to balance the osmotic influx resulting from the presence of solutes in the xylem. But at the top of the tree Ψ_p < 0.

What does it mean for the pressure to be < 0?

At the top of the xylem, the higher concentration of solutes in the leaf cells creates an osmotic driving force for water movement into the cells, while gravity creates a driving force for water movement down the tree. Thus, the water is being pulled in two directions, leading plant biologists to describe it as being under “tension.” The water does not pull apart because of the strong hydrogen bonds between water molecules (Chapter 2). Furthermore, because the walls of the xylem conduits are very stiff, even though the water pulls inward on the walls, they resist deformation and exert an outward force on the water.

Now let’s consider what happens during the day when the stomata are open and water is evaporating from the surface of cells within the leaf.

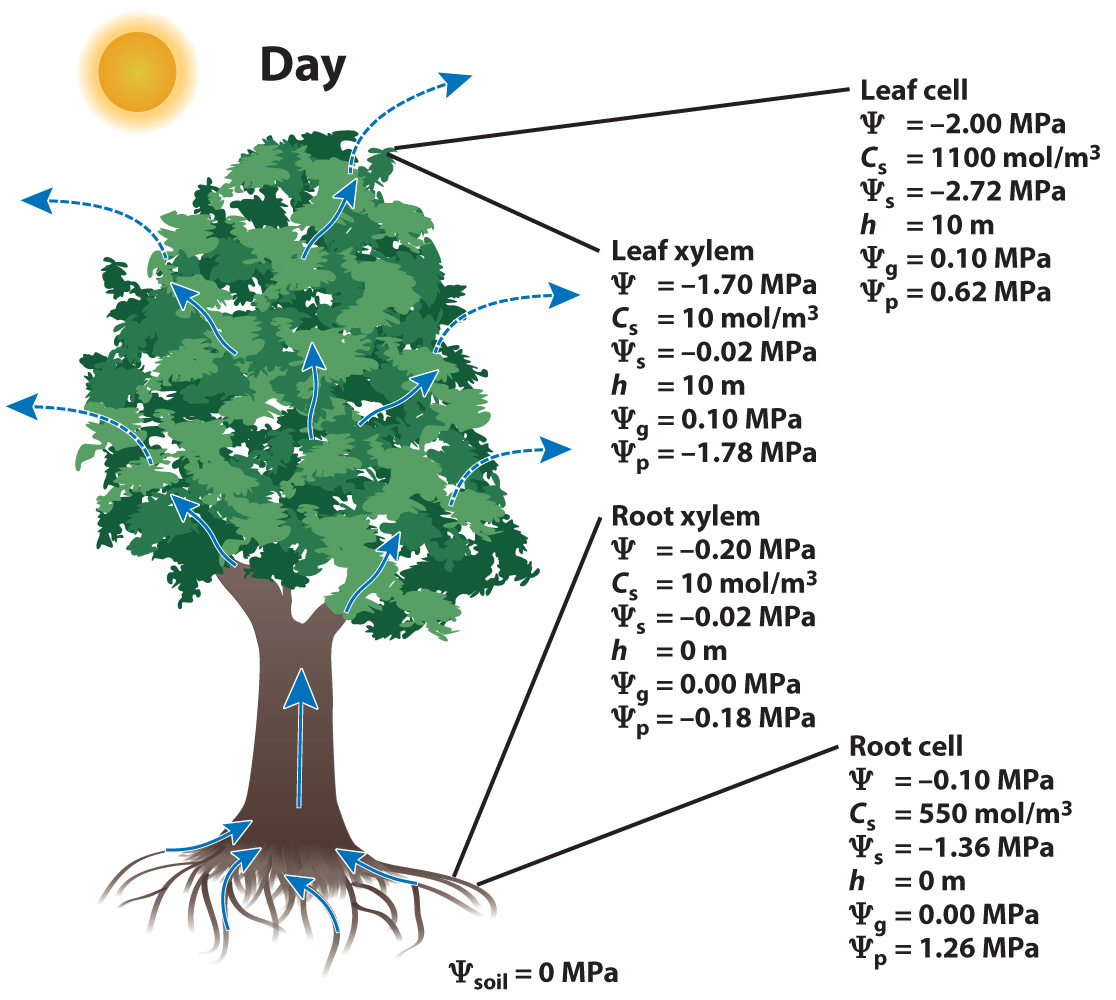
The loss of water from leaf cells causes their Ψ to fall due both to the solutes becoming more concentrated as water is lost and to the cell walls relaxing as cell volume shrinks. This decrease in Ψ causes water to flow into the leaf cells from the xylem.

The movement of water from the xylem to the leaf cells causes the Ψ in the leaf xylem to fall. This drop in Ψ in leaf xylem then creates the gradient in water potential that drives the flow of water through the tree. Note that because Ψ_s and Ψ_g remain unchanged in the xylem, the difference in Ψ_xylem from the roots to the leaves is due to a decrease in the pressure (Ψ_p) at the top of the plant.

Thus, the answer to our question of what is responsible for the movement of water up a tree is that transpiration leads to a decrease in the pressure in the xylem and this difference in the pressure at the top and the bottom of the trees drives the flow of water through the xylem.

Note that in our transpiring tree, the difference in Ψ_p between the bottom and the top of the xylem is large, many times the difference in Ψ_g. A large pressure difference is needed to overcome the energy losses due to friction (viscous drag) of the water flowing through the xylem conduits. How large a pressure difference is needed depends on both the structure of the xylem (water flows more easily through larger diameter conduits) and the flow rate needed to balance water losses due to transpiration.