Chapter 1. Working With Data 21.4

Working with Data: HOW DO WE KNOW? Fig. 21.4

Fig. 21.4 describes the process by which researchers commonly study allele frequencies in a population. Answer the questions after the figure to practice interpreting data and understanding experimental design. Some of these questions refer to concepts that are explained in the following three brief data analysis primers from a set of four available on LaunchPad:

Experimental Design
Data and Data Presentation
Statistics

You can find these primers by clicking on the button labeled “Resources” in the menu at the upper right on your main LaunchPad page. Within the following questions, click on “Primer Section” to read the relevant section from these primers. Click on the button labeled “Key Terms” to see pop-up definitions of boldfaced terms.

HOW DO WE KNOW?

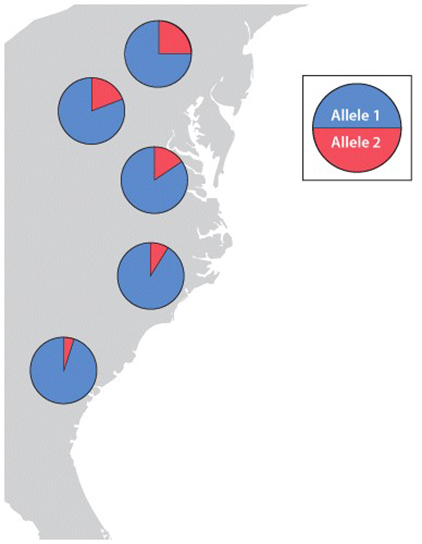
FIG. 21.4: How is genetic variation measured?

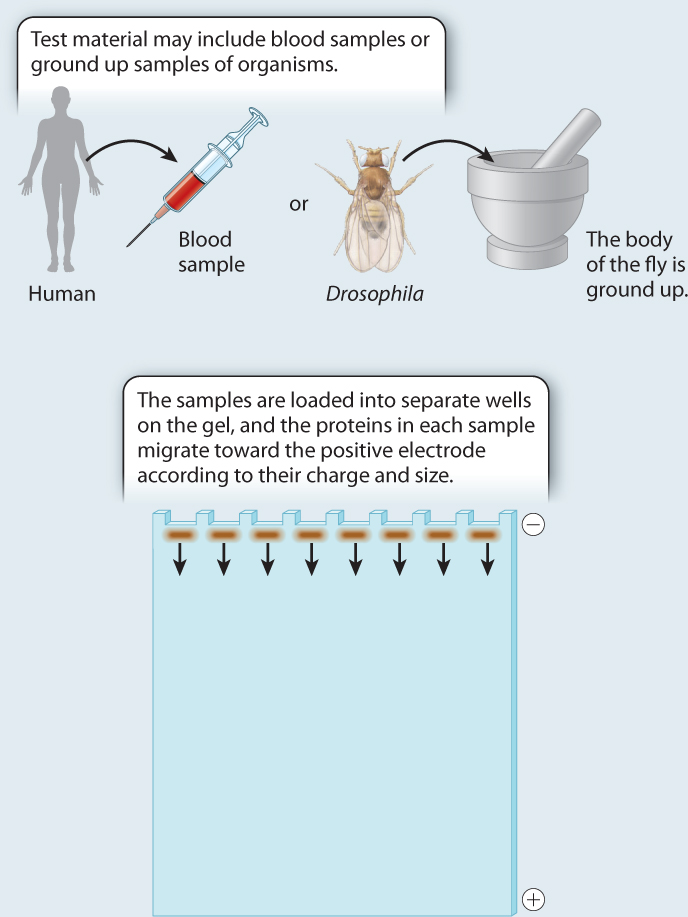
BACKGROUND The introduction of protein gel electrophoresis in 1966 gave researchers the opportunity to identify differences in amino acid sequence in proteins both among individuals and, in the case of heterozygotes, within individuals. Proteins with different amino acid sequences run at different rates through a gel in an electric field. Often, a single amino acid difference is enough to affect the mobility of a protein in a gel.

METHOD Starting with crude tissue—the whole body of a fruit fly, or a blood sample from a human—we load the material on a gel, and turn on the current. The rate at which a protein migrates depends on its size and charge, both of which may be affected by its amino acid sequence. To visualize the protein at the end of the gel run, we use a biochemical indicator that produces a stain when the protein of interest is active. The result is a series of bands on the gel.

RESULTS The genotypes of eight individuals for a gene with two alleles are analyzed. Four are allele 1 homozygotes; two are allele 2 homozygotes; and two are heterozygotes. Note that the heterozygotes do not stain as strongly on the gel because each band has half the intensity of the single band in the homozygote. We can measure the allele frequencies simply by counting the alleles. Each homozygote has two of the same allele, and each heterozygote has one of each.

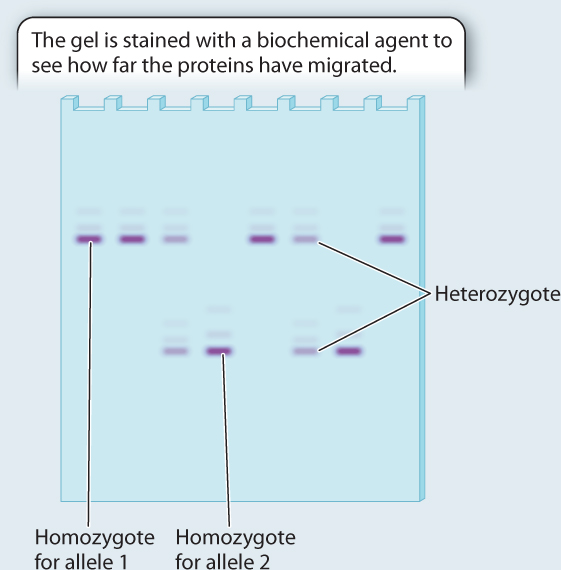
Total number of alleles in the population = 8 × 2 = 16

Number of allele 1 in the population = 2 × (number of allele 1 homozygotes) + (number of heterozygotes) = 8 + 2 = 10

Frequency of allele $1=\frac{10}{16}= \frac{5}{8}$

Number of allele 2 in the population = 2 × (number of allele 2 homozygotes) + (number of heterozygotes) = 4 + 2 = 6

Frequency of allele $2=\frac{6}{16}= \frac{3}{8}$

Note that the two allele frequencies add to 1.

CONCLUSION We now have a profile of genetic variation at this gene for these individuals. Population genetics involves comparing data such as these with data collected from other populations to determine the forces shaping patterns of genetic variation.

FOLLOW-UP WORK This technique is seldom used these days because it is easy now to recover much more detailed genetic information about genetic variation from DNA sequencing.

SOURCE Lewontin, R. C., and J. L. Hubby. 1966. “A Molecular Approach to the Study of Genic heterozygosity in natural populations. II. Amount of variation and degree of heterozygosity in natural populations of Drosophila pseudoobscura.” Genetics 54:595–609.

Question 1 of 8

Question

In a new experiment using the same eight fruit flies from a single population that were used in the study in Fig. 21.4, we study protein variation at another locus, Locus II. Like the first locus, Locus II has two common alleles, which can be separated by gel electrophoresis, with the slower allele designated “S” and the faster one “F”. Here is the gel:

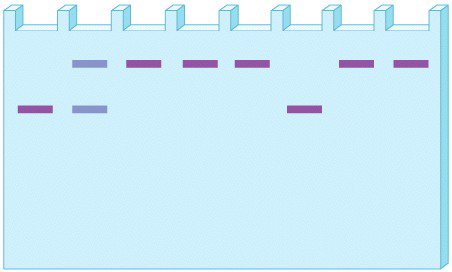
What are the allele frequencies for each allele?

S 6/8, F 3/8

S 6/8, F 2/8

S 5/8, F 3/8

S 11/16, F 5/16

S 21/32, F 9/32

Correct.

Incorrect.

Incorrect. Please try again.

Question 3 of 8

Question

We carry out the same study as in Fig. 21.4 on the same locus, but with four individuals from a different population of the same species. We find in the sample from the second population that the allele frequencies are 0.75 for allele 1 and 0.25 for allele 2. Do these variations from the findings shown in Fig. 21.4 imply that there are allele frequency differences between the two populations?

No, the sample sizes are too small to obtain an accurate assessment of the allele frequencies in each population.

No, even though the bands on the gels are in approximately the same place on the gels, we cannot assume they represent the same alleles in each population.

No, because different forces are acting on allele frequencies in each population, so the similarity in allele frequencies is a coincidence.

Yes, there are more allele 1’s in the second population than there are in the first population.

Yes, because allele frequencies inevitably carry from one population to another because of differences in environmental conditions.

Correct.

Incorrect.

Incorrect. Please try again.

sample

The set of objects or events chosen from a larger population from which observations are taken. Typically, sampling is done randomly to ensure that the sample is representative of the total population of objects or events.

Table

Data and Data Presentation

Collecting Data

We can collect data as part of an experiment. For example, we vary the nutrients added to cells in culture to see which are critical for cell proliferation, and count the number of cells after a specified period in each of the different experimental treatments. Or data collection may be exploratory. For example, if we are interested in what mammal species are present in a remote patch of forest, we can simply record what we see as we walk through the forest. The tools needed for data collection vary correspondingly, ranging from expensive, sophisticated scientific hardware to a notebook and a pencil.

Nowadays computers often collect data automatically, meaning that it is possible to accumulate vast quantities of data. With our ability to sequence DNA cheaply and efficiently, genomic data—long strings of A’s, G’s, C’s, and T’s—is an example of the current explosion of mega-datasets. Satellite imagery, as well, supplies a vast reservoir of data about our planet.

Almost always, data represent a sample. We assume that the cells in our experiment are representative of the appropriate class of cells in general, and we assume that the animals we saw in the forest patch are representative of all the animals present in the forest. With this in mind, we have to be careful in designing our method of collecting data. Imagine, for example, that in determining what mammal species live in our patch of forest, we only visited the forest during daylight hours. Any claim to have assessed the forest for all of its inhabitants then is inaccurate because we have overlooked nocturnal species.

Data sometimes need to be weeded. A freak result in one experiment, for example, might have been caused by contamination and should be removed from the analysis because the result is produced by factors unrelated to what we are investigating. Imagine, for example, that we encounter a domestic cat belonging to a local resident in our forest mammal inventory. Given that we are interested in the native mammals, we should exclude this intruder from our data. Data weeding, however, is a tricky area. It is important only to exclude data that are clearly problematic rather than simply eliminating the data that seem to contradict our hypothesis!

Question 5 of 8

Question

In a study of another locus, also with two alleles designated Allele 1 and Allele 2, over several degrees of latitude in North America, the results are presented using pie charts, below.

What can we conclude from this data?

Allele 1 is better adapted to southern latitudes.

Allele 1 frequency is positively correlated with latitude.

The sample sizes are too small to permit any inferences about the impact of geography on allele frequencies.

Allele 1 frequency shows regression to the mean.

Allele 1 frequency varies randomly from one population to the next.

Correct.

Incorrect.

Incorrect. Please try again.

pie chart

A method of presenting data by dividing a circle into “slices,” each representing the proportion of the total contributed by a particular category.

Table

Data and Data Presentation

Graphing Data

Now we can be confident that our numbers are reliable. The next challenge is to present the data. Typically we do this with a graph. Different kinds of data lend themselves to different kinds of graphs. Our mammal species data is discrete—we have clear categories: A, B, C, D, E, and F. For discrete data, either a pie chart or a bar graph would be appropriate. A pie chart divides a circle into “cake slices,” each representing the proportion of the total contributed by a particular category. In our trapping study, we have a total of 61 animals, so the slice representing species A will make an angle at the center of the pie of 17/61 x 360 = 100°. A bar graph represents the frequency of each species as a column whose height is proportional to frequency.

Fig. 1

What about continuous data? Imagine that the data we collected is the body lengths of the mammals we trapped. In this case, we might choose a histogram, which looks similar to a bar chart; only here we have to impose our own categories on a continuum of data. Because they were discrete categories—different species—the columns in the bar graph may have gaps between them. In the histogram, by contrast, there are no gaps between the columns because the end of one range (1–20cm) is continuous with the beginning of the next (20–40cm).

Fig. 2

Often we are plotting two variables against each other. If, for example, we record the time of day that each mammal is trapped, we can plot the total number of mammals trapped over the course of the 24-hour period.

	Midnight-2am	2am-4am	4am-6am	6am-8am	8am-10am	10am-12am	12am-2pm	2pm-4pm	4pm-6pm	6pm-8pm	8pm-10pm	10pm-midnight
Number trapped	8	3	2	0	0	0	0	0	1	22	17	8
Cumulative number	8	11	13	13	13	13	13	13	14	36	53	61

Table

Often one variable is independent—time, for example, will elapse regardless of the mammal count. We plot this on the x-axis, the horizontal axis of the graph. The dependent variable—the values that vary as a function of the independent variable (in this case, time of day)—is plotted on the y-axis, the vertical axis of the graph. If there is reason to believe that consecutive measurements are related to each other, points can be connected to each other by a line. Plotting our data on a graph using the values of the independent and dependent variables as coordinates gives us a line graph. This is a good way to identify trends and patterns in data. Here we can see that the mammals in our forest plot tend to be inactive (and therefore unlikely to be trapped) during daylight hours.

Fig. 3

In science, data are typically presented as a scatterplot, in which points are specified by their (x,y) coordinates. Points are not joined to each other by lines unless there are specified connections among them. Here, plotted in a way similar to the line graph (with the independent variable on the x-axis) is a scatterplot showing the time taken to drive from home to campus for a large number of students. The independent variable is the distance traveled; the dependent variable is travel time because the distances are fixed but travel times vary. Overall, there is a positive correlation between travel time and distance (the further you live from campus, the longer, on average, it will take you to get there), but there is plenty of variation as well. Look at the eight points representing the eight students who live five miles from campus. The variation we see in travel time (from 6 minutes to 30 minutes) is a reflection of differences in driving speed, traffic conditions, and route.

Fig. 4

What if there are more than two variables? Three-dimensional plots can be informative (but can also cause the reader headaches). A popular modern solution to this problem is a so-called temperature plot, in which the third dimension is represented in two dimensions through color: red (hot) for a strong effect in the third dimension and blue (cool) for a weak effect.

Graphs are the mainstay of scientific presentation, but you will see many other ways of presenting data in your textbook. For example, studies showing how different genes interact with each other in the course of development are often illustrated using network diagrams that give the reader a direct sense of the “connectedness” of a particular gene (or node). Evolutionary trees reveal the branching pattern of evolution with species that are closely related having a more recent common ancestor than those that are more distantly related.

Methods of presenting data in science are not limited, even in textbooks, by standard approaches. The popular press has developed many graphics-intense ways of presenting data. Think of an electoral map after an election. You can view information on a number of levels: whether the state is red or blue, the name of the election winner, the size of his or her majority, and so on. Scientists are learning that they too can package information in ways that are simultaneously informative and attractive.

Question 6 of 8

Question

On the basis of laboratory experiments on fruit flies raised under different conditions, researchers hypothesize that Allele 1 at a particular locus with two alleles is advantageous in dry climates. How would you best test this idea with samples from wild fruit fly populations?

Compare Allele frequencies between one desert population and one rainforest population.

Compare Allele frequencies among multiple desert populations and multiple rainforest populations.

Compare Allele 1 frequencies to Allele 2 frequencies in a desert population.

Compare Allele 1 frequencies to Allele 2 frequencies in rainforest populations.

Sample desert populations along a latitudinal gradient.

Correct.

Incorrect.

Incorrect. Please try again.

hypothesis

A tentative explanation for one or more observations that makes predictions that can be tested by experiments or additional observations.

Table

Experimental Design

Types of Hypotheses

A hypothesis, as we saw in Chapter 1, is a tentative answer to the question, an expectation of what the results might be. This might at first seem counterintuitive. Science, after all, is supposed to be unbiased, so why should you expect any particular result at all? The answer is that it helps to organize the experimental setup and interpretation of the data.

Let’s consider a simple example. We design a new medicine and hypothesize that it can be used to treat headaches. This hypothesis is not just a hunch—it is based on previous observations or experiments. For example, we might observe that the chemical structure of the medicine is similar to other drugs that we already know are used to treat headaches. If we went into the experiment with no expectation at all, it would be unclear what to measure.

A hypothesis is considered tentative because we don’t know what the answer is. The answer has to wait until we conduct the experiment and look at the data. When an experiment predicts a specific effect, as in the case of the new medicine, it is typical to also state a null hypothesis, which predicts no effect. Hypotheses are never proven, but it is possible based on statistical analysis to reject a hypothesis. When a null hypothesis is rejected, the hypothesis gains support.

Sometimes, we formulate several alternative hypotheses to answer a single question. This may be the case when researchers consider different explanations of their data. Let’s say for example that we discover a protein that represses the expression of a gene. Our question might be: How does the protein repress the expression of the gene? In this case, we might come up with several models—the protein might block transcription, it might block translation, or it might interfere with the function of the protein product of the gene. Each of these models is an alternative hypothesis, one or more of which might be correct.

Question 7 of 8

Question

In another study, we take samples of fruit flies from two populations living on neighboring banana plantations in Central America, with 10 individuals in each sample. We determine the allele frequencies in the two samples and find them to be different. We then do a statistical test to see whether this difference is statistically significant. Our result states that the “the probability that the observed differences between the samples arose by chance is p = 0.17.” What can we conclude?

The two samples are 17% different.

The two samples are 17% identical.

The two samples are not significantly different.

The two samples are significantly different.

Conditions differ significantly between the two populations.

Correct.

Incorrect.

Incorrect. Please try again.

statistical test	A test used to distinguish accidental or weak relations from real and strong ones.
P-value	The likelihood that an observed result (or a result more extreme than that observed) could have been observed merely by chance. If P ≤ 0.05, the observed results are conventionally regarded as unlikely to be attributed to chance alone.

Table

Statistics

Statistical Significance

Biologists observe many relations between variables that are either due to chance in the sample that happened to be chosen or that are too weak to be biologically important. To distinguish the accidental or weak relations from the real and strong ones, a statistical test of the relation is carried out. A statistical test must be based on some specific hypothesis. For example, to determine whether an observed correlation coefficient could be due to chance, we might carry out a statistical test of the hypothesis that the true correlation coefficient is 0. A statistical test usually yields a single number, usually called the P-value (or sometimes p-value), that expresses the likelihood that an observed result (such as a correlation coefficient) could have been observed merely by chance. A P-value is a probability, and if P ≤ 0.05 the observed results are conventionally regarded as unlikely to be attributed to chance alone. In that case, the observed relation is likely to be genuine. In other words, if an observed relation would be obtained by chance alone in only 1 in 20 or fewer experiments (P ≤ 0.05), then the observed relation is regarded as likely to be true. A finding of P ≤ 0.01 is taken as even stronger evidence that the observed result is unlikely to be due to chance.

Figure 6

Statistical testing is necessary because different researchers may disagree on whether or not a finding supports a particular hypothesis or if the interpretation of a result could be affected by wishful thinking. Take Figure 6, for example. If you wish to believe that there was a functional relation between xand y, you might easily convince yourself that the 20 data points fit the straight line. But in fact the P value of the regression coefficient is about P = 0.25, which means that about 25% of the time you would get a line that fits the data as well or better than the line you observed, purely by chance. The proper conclusion is that these data give no support for the hypothesis of a functional relation between x and y. If there is such a relation, then it is too weak to show up in a sample of only 20 pairs of points.

There is good reason to be cautious even when a result is statistically significant. Bear in mind that 5% of statistical tests are misleading in that they indicate that some result is significant merely as a matter of chance. For example, over any short period of time, about 5% of companies listed in stock exchanges will have changes in the dollar value of their shares that are significantly correlated with changes in the number of sunspots, even though the correlation is certainly spurious and due to chance alone. Critical thinking therefore requires that one maintain some skepticism even when faced with statistically significant results published in peer-reviewed scientific journals. Scientific proof rarely hinges on the result of a single experiment, measurement, or observation. It is the accumulation of evidence from many independent sources, all pointing in the same direction, that lends increasing credence to a scientific hypothesis until eventually it becomes a theory.

Question 8 of 8

Question

In another fruit fly population sampling study, we compare allele frequencies from a population from Panama and from a population from Rhode Island. Because of import restrictions imposed by the U.S. government, we can only bring in four fruit flies from Panama, so, to keep the sample sizes consistent, we also analyze only four flies from Rhode Island. Allele frequencies differ between the two populations, but statistical testing indicates that the difference is not statistically significant. What is the null hypothesis that we have tested?

Similar selective factors affect alleles at this locus in both Panama and Rhode Island populations.

Different selective factors affect alleles at this locus in Panama and Rhode Island populations.

Geography has no effect on allele frequencies.

The fruit flies were sampled from different populations.

Sample size determines statistical significance.

Correct.

Incorrect.

Incorrect. Please try again.

null hypothesis

A hypothesis that is to be tested, often one that predicts no effect.

Table

Experimental Design

Types of Hypotheses

Sample	Original	2	3	4	5
Frequency of allele 1	0.625	0.75	0.75	0.875	1.0
Latitude (degrees north of the equator)	23	26	29	31	36