Chapter 1. Working With Data 36.20

Working with Data: HOW DO WE KNOW? Fig. 36.20

Figure 36.20 describes experiments that were conducted to understand how the retina of a mammal processes light information. Answer the questions after the figure to practice interpreting data and understanding experimental design. These questions refer to concepts that are explained in the following three brief data analysis primers from a set of four available on LaunchPad.

Experimental Design
Data and Data Presentation
Statistics

You can find these primers by clicking on the button labeled “Resources” in the menu at the upper right on your main LaunchPad page, then select “Content by type.” Within the following questions, click on “Primer Section” to read the relevant section from these primers. Click on the button labeled “Key Terms” to see pop-up definitions of boldfaced terms.

HOW DO WE KNOW?

FIG. 36.20: How does the retina process visual information?

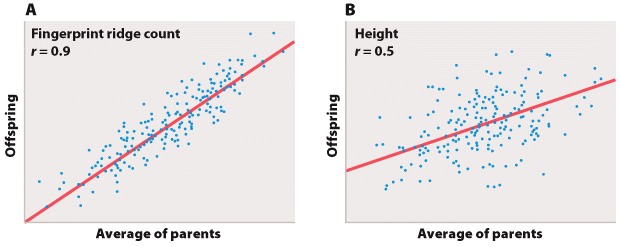
BACKGROUND In the 1950s, the American neurophysiologist Stephen Kuffler was interested in understanding how the retina helps to process light information before it is sent to the brain. He focused on the activity of ganglion cells in the retina because they receive input from the photoreceptors and bipolar cells.

EXPERIMENT Kuffler stimulated different regions of the cat’s retina with localized points of light while recording the action potentials produced by ganglion cells.

RESULTS Kuffler found that there are two types of ganglion cell: on-center and off-center cells. On-center ganglion cells fire more action potentials when light shines on the center of the cell’s receptive field compared to the surrounding region, and off-center cells fire more when light is shown in the periphery and less on the center. These patterns are explained by lateral inhibition of input to the ganglion cells by the photoreceptors and bipolar neurons in the retina.

FOLLOW-UP WORK In the 1960s, Hubel and Wiesel found similar center–surround neural receptive fields, though with enhanced opposition, in part of the thalamus and in the visual cortex of the brain. Cells with these fields enable cats and other mammals to detect shapes of a given orientation moving through their visual field. Similar center–surround receptive fields have also been found in the somatosensory and auditory cortex, highlighting the use of lateral inhibition to enhance sensory acuity and edge detection. Other studies have found similar center–surround sensory processing in invertebrates and other vertebrates.

SOURCE Kuffler, S. W. 1953. “Discharge Patterns and Functional Organization of Mammalian Retina.” Journal of Neurophysiology 16 : 37–68; Hubel, D. H. 1963. “The Visual Cortex of the Brain.” Scientific American 209 : 54–62.

Question 1 of 8

Question

Below in Fig. 1 is a graph of the firing frequency of an “on-center” ganglion cell in response to changes in light intensity directed at the central region of its receptive field.

Figure 1

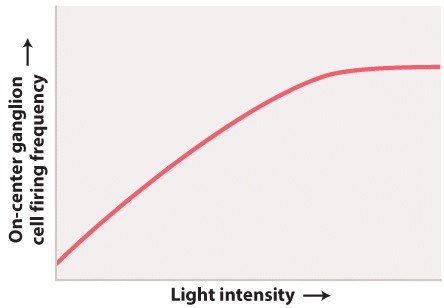
What is the independent variable?

the firing frequency of the on-center ganglion

light intensity

the membrane voltage of the ganglion cell.

A and C

none of the above

Correct.

Incorrect.

Incorrect. Please try again.

independent variable

The manipulation performed on the test group by the researchers.

Table

Experimental Design

Testing Hypotheses: Variables

When performing experiments, researchers manipulate the test group differently from the control groups. This difference is known as a variable. There are two types of variables. An independent variable is the manipulation performed on the test group by the researchers. It is considered “independent” because the researchers could choose any variable they wish. The dependent variable is the effect that is being measured. It is considered “dependent” because the expectation is that it depends on the variable that was changed. In our example of the headache medicine, the independent variable is the type of medicine (new medicine, no medicine, placebo, or medicine known to be effective). The dependent variable is the presence or absence of headache following treatment.

In designing experiments, there is an additional issue to consider: the size of each of our groups. In order to draw conclusions from our data, we need to make sure that our results are valid and reproducible, and not merely the result of chance. One way to minimize the effect of chance is to include a large number of patients in each group. How many? The sample size is the number of independent data points and is determined based on probability and statistics, the subject of the next primer.

Question 3 of 8

Question

In Fig. 36.20, recordings of the off-center ganglion cell are needed in order:

to have a control for interpreting the response of the on-center ganglion cell.

to show that two different retinal ganglion cells exist to detect changes in light intensity across the cat’s visual field.

to show that the two types of ganglion cells receive the same pattern of synaptic input from retinal light receptors (rod cells) .

to show that the two types of ganglion cells receive a different pattern of synaptic input from retinal light receptors (rod cells) .

A and B

B and D

none of the above

Correct.

Incorrect.

Incorrect. Please try again.

control

Operations or observations that are set up in advance in such a way that the researcher knows in advance what result should be expected if everything in the study is working properly.

Table

Experimental Design

Testing Hypotheses: Controls

Hypotheses can be tested in various ways. One way is through additional observations. There are a large number of endemic species on the Galápagos Islands. We might ask why and hypothesize that it has something to do with the location of the islands relative to the mainland. To test our hypothesis, we might make additional observations. We could count the number of endemic species on many different islands, calculate the size of each of these islands, and measure the distance from the nearest mainland. From these observations, we can understand the conditions that lead to endemic species on islands.

Hypotheses can also be tested through controlled experiments. In a controlled experiment, several different groups are tested simultaneously, keeping as many variables the same among them. In one group, a single variable is changed, allowing the researcher to see if that variable has an effect on the results of the experiment. This is called the test group. In another group, the variable is not changed and no effect is expected. This group is called the negative control. Finally, in a third group, a variable is introduced that has a known effect to be sure that the experiment is working properly. This group is called the positive control.

Controls such as negative and positive control groups are operations or observations that are set up in such a way that the researcher knows in advance what result should be expected if everything in the study is working properly. Controls are performed at the same time and under the same conditions as an experiment to verify the reliability of the components of the experiment, the methods, and analysis.

For example, going back to our example of a new medicine that might be effective against headaches, you could design an experiment in which there are three groups of patients—one group receives the medicine (the test group), one group receives no medicine (the negative control group), and one group receives a medicine that is already known to be effective against headaches (the positive control group). All of the other variables, such as age, gender, and socioeconomic background, would be similar among the three groups.

These three groups help the researchers to make sense of the data. Imagine for a moment that there was just the test group with no control groups, and the headaches went away after treatment. You might conclude that the medicine alleviates headaches. But perhaps the headaches just went away on their own. The negative control group helps you to see what would happen without the medicine so you can determine which effects in the test group are due solely to the medicine.

In some cases, researchers control not just for the medicine (one group receives medicine and one does not), but also for the act of giving a medicine. In this case, one negative control involves giving no medicine, and another involves giving a placebo, which is a sugar pill with no physiological effect. In this way, the researchers control for the potential variable of taking medication. In general, for a controlled experiment, it is important to be sure that there is only one difference between the test and control groups.

Question 4 of 8

Question

In related experiments, different on-center ganglion cells were stimulated in their central region with light of varying intensity, and different auditory ganglion cells were stimulated with sounds of varying intensity, yielding the data in Fig. 2 below.

Figure 2

The red lines are regression lines of ganglion cell firing frequency on (A) light intensity and (B) sound intensity.

These results indicate:

that firing frequency is uncorrelated with light intensity but is correlated with sound intensity.

that firing frequency varies more strongly with sound intensity than with light intensity.

that the correlation of firing frequency with light intensity is greater than the correlation of firing frequency with sound intensity.

that firing frequency varies more strongly with light intensity than with sound intensity.

B and C

A and D

Correct.

Incorrect.

Incorrect. Please try again.

regression line	A line drawn on a scatterplot that depicts how, on average, the variable y changes as a function of the variable x across the whole set of data.
correlation	An association between variables such that as one variable increases the other increases, or as one variable increases the other decreases.

Table

Statistics

Correlation and Regression

Biologists often are also interested in the relation between two different measurements, such as height and weight or number of species on an island versus the size of the island. Such data are often depicted as a scatter plot (Figure 5), in which the magnitude of one variable is plotted along the x-axis and the other along the y-axis, each point representing one paired observation.

Figures 5a and 5b

Figure 5A is the sort of data that would correspond to fingerprint ridge count (the number of raised skin ridges lying between two reference points in each fingerprint). While the data show some scatter, the overall trend is evident. There is a very strong association between the average fingerprint ridge count of parents and that of their offspring. The strength of association between two variables can be measured by the correlation coefficient, which theoretically ranges between +1 and –1. A correlation coefficient of +1 means a perfect positive relation (as one variable increases, the other increases proportionally), and a correlation coefficient of –1 implies a perfect negative relation (as one variable increases, the other decreases proportionally). Correlation coefficients of +1 or –1 are rarely observed in real data. In the case of fingerprint ridge count, the correlation coefficient is 0.9, which implies that the average fingerprint ridge count of offspring is almost (but not quite) equal to that of the parents. For a complex trait, this is a remarkably strong correlation.

Figure 5B represents data that would correspond to adult height. The data exhibit greater scatter than in Figure 5A; however, there is still a fairly strong resemblance between parents and offspring. The correlation coefficient in this case is 0.5. This value means that, on average, the offspring height is approximately halfway between that of the average of the parents and the average of the population as a whole.

The illustrations in Figure 5A and 5B also emphasize one limitation of the correlation coefficient. The correlation coefficient measures the strength of a straight-line (linear) relation. A nonlinear relation (one curving upward or downward) between two variables could be quite strong, but the data might still show a weak correlation.

Each of the straight lines in Figure 5 is a regression line or, more precisely, a regression line of y on x. Each line depicts how, on average, the variable y changes as a function of the variable x across the whole set of data. The slope of the line tells you how many units y changes, on average, for a unit change in x. A slope of +1 implies that a one-unit change in x results in a one-unit change in y, and a slope of 0 implies that the value of x has no effect on the value of y. The slope of a straight line relating values of y to those of x is known as the regression coefficient.

Question 5 of 8

Question

The data plotted in the graphs in question 4 represent

continuous data

discrete data

repeated trials of a given retinal or auditory ganglion cell

qualitative data

none of the above

Correct.

Incorrect.

Incorrect. Please try again.

continuous data	Data that are measured and can take any value.
discrete data	Data that are counted and can take only certain values.
qualitative data	Descriptive data.

Table

Data and Data Presentation

Kinds of Data

Data come in several fundamentally different forms:

Qualitative data are descriptive; quantitative data are expressed numerically. Discrete data are counted and can only take certain values; continuous data are measured and can take any value. In general in science, we are dealing with quantitative data because they lead to more and more powerful methods of analysis. In particular, quantitative data lend themselves to statistical analysis. With the quantitative data gathered on the height of our corn stems, for example, we can calculate the average height of all the stems in the field. Data that may appear superficially qualitative is accordingly often transformed into quantitative data. To take a familiar example, in surveys you may be given a statement and asked whether you “Strongly Agree, Agree, Disagree, or Strongly Disagree.” These are qualitative assessments, but they are converted into quantitative data by giving each category a numerical score: Strongly Agree = 4, Agree = 3, Disagree = 2, Strongly Disagree = 1. With these numerical scores, we can summarize the results of the survey statistically. For example, we can compare our survey’s average with the averages from similar surveys carried out over different years or in different countries to see if responses vary by time and place.