Chapter 1. Working With Data 16.14
Working with Data: HOW DO WE KNOW? Fig. 16.14
Fig. 16.14 describes the conclusions that Mendel drew after conducting numerous crosses between pea plants. Answer the questions after the figure to practice interpreting data and understanding experimental design. These questions refer to concepts that are explained in one of four brief data analysis primers--the primer called “Statistics.” You can find these primers by clicking on the button labeled “Resources” in the menu at the upper right on your main LaunchPad page. Within the following questions, click on “Primer Section” to read the relevant section from these primers. Click on “Key Terms” to see pop-up definitions of boldfaced terms.

The numbers of yellow seeds and green seeds produced by 20 individual plants were reported by Mendel in the following data:
| Plant number | Number of pods | Total seeds | Average number of seeds per pod | Proportion green seeds |
|---|---|---|---|---|
| 1 | 8 | 57 | 7.1 | 0.21 |
| 2 | 6 | 36 | 6.0 | 0.31 |
| 3 | 6 | 35 | 5.8 | 0.23 |
| 4 | 6 | 39 | 6.5 | 0.18 |
| 5 | 3 | 31 | 10.3 | 0.23 |
| 6 | 2 | 19 | 9.5 | 0.26 |
| 7 | 3 | 29 | 9.7 | 0.34 |
| 8 | 8 | 97 | 2.1 | 0.28 |
| 9 | 6 | 43 | 7.2 | 0.26 |
| 10 | 6 | 37 | 6.2 | 0.35 |
| 11 | 4 | 32 | 8.0 | 0.19 |
| 12 | 3 | 26 | 8.7 | 0.23 |
| 13 | 10 | 112 | 11.2 | 0.21 |
| 14 | 7 | 45 | 6.4 | 0.29 |
| 15 | 4 | 32 | 8.0 | 0.31 |
| 16 | 7 | 53 | 7.6 | 0.17 |
| 17 | 5 | 34 | 6.8 | 0.18 |
| 18 | 8 | 64 | 8.0 | 0.22 |
| 19 | 4 | 32 | 8.0 | 0.22 |
| 20 | 8 | 62 | 7.8 | 0.29 |
Question
Estimate the mean and standard deviation of the number of pods per plant.
| A. |
| B. |
| C. |
| D. |
| mean | The arithmetic average of all the measurements (all the measurements added together and the result divided by the number of measurements); the peak of a normal distribution along the x-axis. |
| standard deviation | The extent to which most of the measurements are clustered near the mean. To obtain the standard deviation, you calculate the difference between each individual measurement and the mean, square the difference, add these squares across the entire sample, divide by n – 1, and take the square root of the result. |
Statistics
The Normal Distribution

The first step in statistical analysis of data is usually to prepare some visual representation. In the case of height, this is easily done by grouping nearby heights together and plotting the result as a histogram like that shown in Figure 1. The smooth, bell-shaped curve approximating the histogram in Figure 1A is called the normal distribution. If you measured the height of more and more individuals, then you could make the width of each bar in the histogram narrower and narrower, and the shape of the histogram would gradually get closer and closer to the normal distribution.

The normal distribution does not arise by accident but is a consequence of a fundamental principle of statistics which states that when many independent factors act together to determine the magnitude of a trait, the resulting distribution of the trait is normal. Human height is one such trait because it results from the cumulative effect of many different genetic factors as well as environmental effects such as diet and exercise. The cumulative effect of the many independent factors affecting height results in a normal distribution.
The normal distribution appears in countless applications in biology. Its shape is completely determined by two quantities. One is the mean, which tells you the location of the peak of the distribution along the x-axis (Figure 2). While we do not know the mean of the population as a whole, we do know the mean of the sample, which is equal to the arithmetic average of all the measurements—the value of all of the measurements added together and divided by the number of measurements.
In symbols, suppose we sample n individuals and let xi be the value of the ith measurement, where i can take on the values 1, 2, ..., n. Then the mean of the sample (often symbolized ) is given by
, where the symbol
means “sum” and
means x1 + x2 + ... + xn.
For a normal distribution, the mean coincides with another quantity called the median. The median is the value along the x-axis that divides the distribution exactly in two—half the measurements are smaller than the median, and half are larger than the median. The mean of a normal distribution coincides with yet another quantity called the mode. The mode is the value most frequently observed among all the measurements.
The second quantity that characterizes a normal distribution is its standard deviation (“s” in Figure 2), which measures the extent to which most of the measurements are clustered near the mean. A smaller standard deviation means a tighter clustering of the measurements around the mean. The true standard deviation of the entire population is unknown, but we can estimate it from the sample as
What this complicated-looking formula means is that we calculate the difference between each individual measurement and the mean, square the difference, add these squares across the entire sample, divide by n - 1, and take the square root of the result. The division by n - 1 (rather than n) may seem mysterious; however, it has the intuitive explanation that it prevents anyone from trying to estimate a standard deviation based on a single measurement (because in that case n - 1 = 0).
In a normal distribution, approximately 68% of the observations lie within one standard deviation on either side of the mean (Figure 2, light blue), and approximately 95% of the observations lie within two standard deviations on either side of the mean (Figure 2, light and darker blue together). You may recall political polls of likely voters that refer to the margin of error; this is the term that pollsters use for two times the standard deviation. It is the margin within which the pollster can state with 95% confidence the true percentage of likely voters favoring each candidate at the time the poll was conducted.
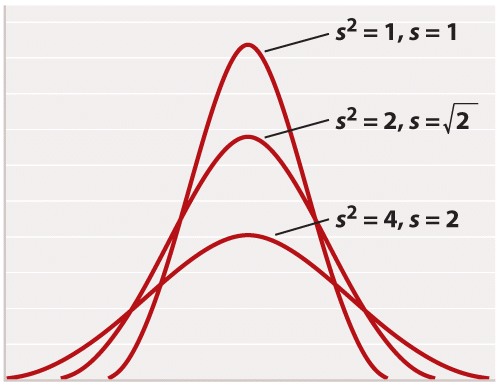
For reasons rooted in the history of statistics, the standard deviation is often stated in terms of s2 rather than s. The square of the standard deviation is called the variance of the distribution. Both the standard deviation and the variance are measures of how closely most data points are clustered around the mean. Not only is the standard deviation more easily interpreted than the variance (Figure 2), but also it is more intuitive in that standard deviation is expressed in the same units as the mean (for example, in the case of height, inches), whereas the variance is expressed in the square of the units (for example, inches2). On the other hand, the variance is the measure of dispersal around the mean that more often arises in statistical theory and the derivation of formulas. Figure 3 shows how increasing variance of a normal distribution corresponds to greater variation of individual values from the mean. Since all of the distributions in Figure 3 are normal, 68% of the values lie within one standard deviation of the mean, and 95% within two standard deviations of the mean.
Another measure of how much the numerical values in a sample are scattered is the range. As its name implies, the range is the difference between the largest and the smallest values in the sample. The range is a less widely used measure of scatter than the standard deviation.