Chapter 1. Working With Data 18.10
Working with Data: HOW DO WE KNOW? Fig. 18.10
Fig. 18.10 describes studies of concordance of traits in twins to determine what traits are mostly genetic in nature and what traits are influenced by the environment. Answer the questions after the figure to practice interpreting data and understanding experimental design. These questions refer to concepts explained in the following two brief data analysis primers from a set of four available on LaunchPad:
- Experimental Design
- Data and Data Presentation
You can find these primers by clicking on the button labeled “Resources” in the menu at the upper right on your main LaunchPad page. Within the following questions, click on “Primer Section” to read the relevant section from these primers. Click on “Key Terms” to see pop-up definitions of boldface terms.
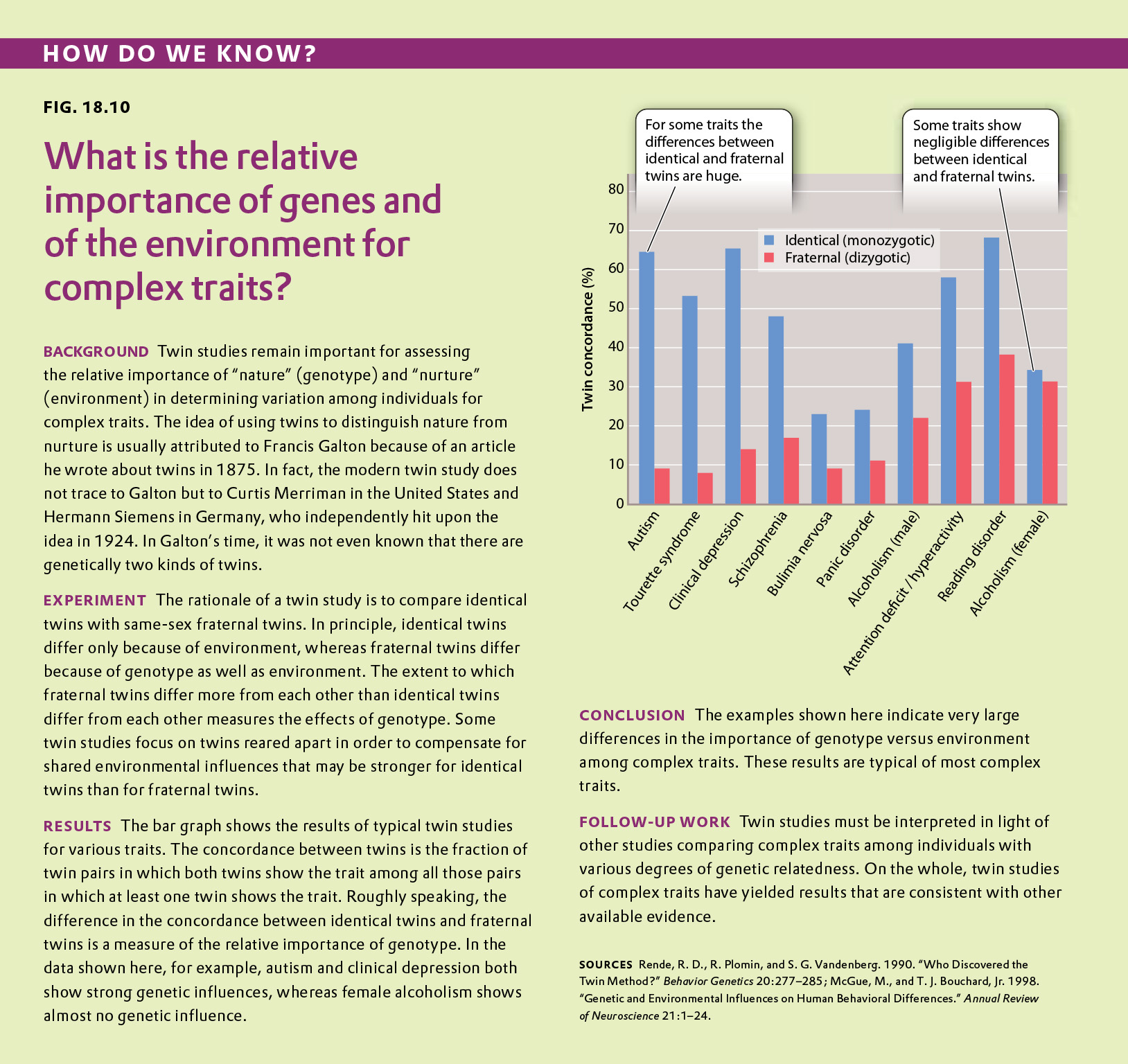
Complex traits are influenced by the interaction between genes and environment. To assess the relative importance of genetics versus environment for any given complex trait, geneticists sometimes study the concordance between identical twins and same-sex fraternal twins. The concordance among twins for any given trait is the proportion of pairs in which both have the trait among those pairs in which at least one has the trait.
Question
On average, what percentage of alleles present in the parents are expected to be shared between identical twins?
| A. |
| B. |
| C. |
| D. |
Question
On average, what percentage of alleles present in the parents are expected to be shared between fraternal twins? (Hint: Imagine that the parental genotypes are A1A2 and A3A4. Start by calculating the average number of alleles expected to be shared between fraternal twins.)
| A. |
| B. |
| C. |
| D. |
Question
In a comparison of identical and fraternal twins, which is the test group and which is the control group?
| A. |
| B. |
| C. |
| D. |
| test group | A group in which a single variable is changed, allowing the researcher to see if that variable has an effect on the results of the experiment. |
| control group | Operations or observations that are set up in such a way that the researcher knows in advance what result should be expected if everything in the study is working properly. |
Experimental Design
Testing Hypotheses: Controls
Hypotheses can be tested in various ways. One way is through additional observations. There are a large number of endemic species on the Galápagos Islands. We might ask why and hypothesize that it has something to do with the location of the islands relative to the mainland. To test our hypothesis, we might make additional observations. We could count the number of endemic species on many different islands, calculate the size of each of these islands, and measure the distance from the nearest mainland. From these observations, we can understand the conditions that lead to endemic species on islands.
Hypotheses can also be tested through controlled experiments. In a controlled experiment, several different groups are tested simultaneously, keeping as many variables the same among them. In one group, a single variable is changed, allowing the researcher to see if that variable has an effect on the results of the experiment. This is called the test group. In another group, the variable is not changed and no effect is expected. This group is called the negative control. Finally, in a third group, a variable is introduced that has a known effect to be sure that the experiment is working properly. This group is called the positive control.
Controls such as negative and positive control groups are operations or observations that are set up in such a way that the researcher knows in advance what result should be expected if everything in the study is working properly. Controls are performed at the same time and under the same conditions as an experiment to verify the reliability of the components of the experiment, the methods, and analysis.
For example, going back to our example of a new medicine that might be effective against headaches, you could design an experiment in which there are three groups of patients—one group receives the medicine (the test group), one group receives no medicine (the negative control group), and one group receives a medicine that is already known to be effective against headaches (the positive control group). All of the other variables, such as age, gender, and socioeconomic background, would be similar among the three groups.
These three groups help the researchers to make sense of the data. Imagine for a moment that there was just the test group with no control groups, and the headaches went away after treatment. You might conclude that the medicine alleviates headaches. But perhaps the headaches just went away on their own. The negative control group helps you to see what would happen without the medicine so you can determine which effects in the test group are due solely to the medicine.
In some cases, researchers control not just for the medicine (one group receives medicine and one does not), but also for the act of giving a medicine. In this case, one negative control involves giving no medicine, and another involves giving a placebo, which is a sugar pill with no physiological effect. In this way, the researchers control for the potential variable of taking medication. In general, for a controlled experiment, it is important to be sure that there is only one difference between the test and control groups.
Question
In a hypothetical study of 50 pairs of fraternal twins, 30 pairs have only one twin exhibiting some trait and 20 pairs have both twins exhibiting the trait. What is the twin concordance in this case?
| A. |
| B. |
| C. |
| D. |
| E. |
Question
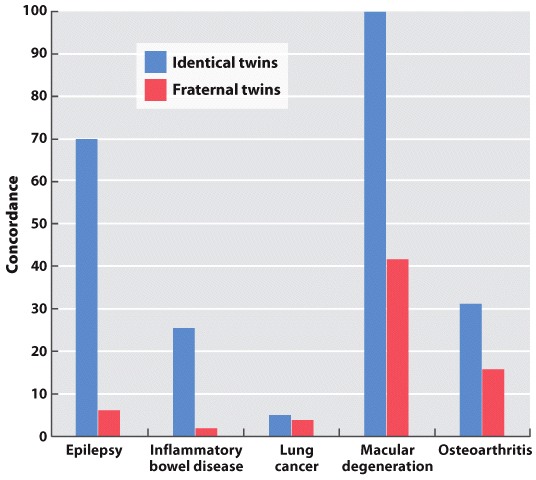
In a study of macular degeneration (an age-related progressive narrowing of the field of vision), 1000 pairs of identical twins were examined. A total of 14 cases were observed in which at least one of the twins was affected, and in all cases both twins were affected. What is the concordance of this trait for identical twins?
| A. |
| B. |
| C. |
| D. |
| E. |
Question
In the same study of macular degeneration described in Question 5, 1000 pairs of fraternal twins were examined. A total of 15 cases were observed in which at least one of the twins was affected, and in six cases both twins were affected. What is the concordance of this trait for fraternal twins?
| A. |
| B. |
| C. |
| D. |
| E. |
Question
Suppose the presence or absence of a trait is determined almost exclusively by genetic differences among individuals. What would you expect the concordance of the trait to be for identical and fraternal twins?
| A. |
| B. |
| C. |
| D. |
Question
Suppose the presence or absence of a trait is determined almost exclusively by environmental differences among individuals. What would you expect the concordance of the trait to be for identical and fraternal twins?
| A. |
| B. |
| C. |
| D. |
Question
The bar graph shown here summarizes twin concordance data for a number of complex traits. Use the graph to answer Questions 9 and 10.
Which of the traits in the bar graph is determined mainly by heredity?
| A. |
| B. |
| C. |
| D. |
| E. |
Data and Data Presentation
Graphing Data
Now we can be confident that our numbers are reliable. The next challenge is to present the data. Typically we do this with a graph. Different kinds of data lend themselves to different kinds of graphs. Our mammal species data is discrete—we have clear categories: A, B, C, D, E, and F. For discrete data, either a pie chart or a bar graph would be appropriate. A pie chart divides a circle into “cake slices,” each representing the proportion of the total contributed by a particular category. In our trapping study, we have a total of 61 animals, so the slice representing species A will make an angle at the center of the pie of 17/61 x 360 = 100°. A bar graph represents the frequency of each species as a column whose height is proportional to frequency.
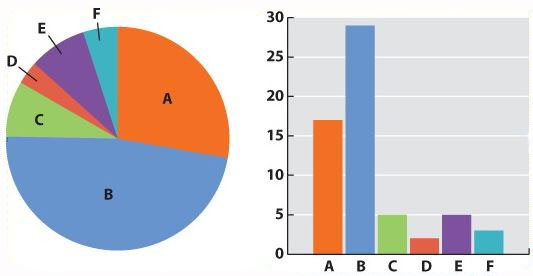
Fig. 1
What about continuous data? Imagine that the data we collected is the body lengths of the mammals we trapped. In this case, we might choose a histogram, which looks similar to a bar chart; only here we have to impose our own categories on a continuum of data. Because they were discrete categories—different species—the columns in the bar graph may have gaps between them. In the histogram, by contrast, there are no gaps between the columns because the end of one range (1–20cm) is continuous with the beginning of the next (20–40cm).
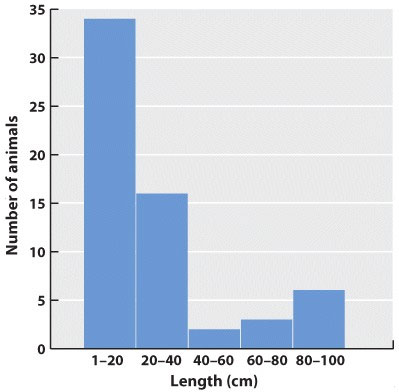
Fig. 2
Often we are plotting two variables against each other. If, for example, we record the time of day that each mammal is trapped, we can plot the total number of mammals trapped over the course of the 24-hour period.
| Midnight-2am | 2am-4am | 4am-6am | 6am-8am | 8am-10am | 10am-12am | 12am-2pm | 2pm-4pm | 4pm-6pm | 6pm-8pm | 8pm-10pm | 10pm-midnight | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number trapped | 8 | 3 | 2 | 0 | 0 | 0 | 0 | 0 | 1 | 22 | 17 | 8 |
| Cumulative number | 8 | 11 | 13 | 13 | 13 | 13 | 13 | 13 | 14 | 36 | 53 | 61 |
Often one variable is independent—time, for example, will elapse regardless of the mammal count. We plot this on the x-axis, the horizontal axis of the graph. The dependent variable—the values that vary as a function of the independent variable (in this case, time of day)—is plotted on the y-axis, the vertical axis of the graph. If there is reason to believe that consecutive measurements are related to each other, points can be connected to each other by a line. Plotting our data on a graph using the values of the independent and dependent variables as coordinates gives us a line graph. This is a good way to identify trends and patterns in data. Here we can see that the mammals in our forest plot tend to be inactive (and therefore unlikely to be trapped) during daylight hours.
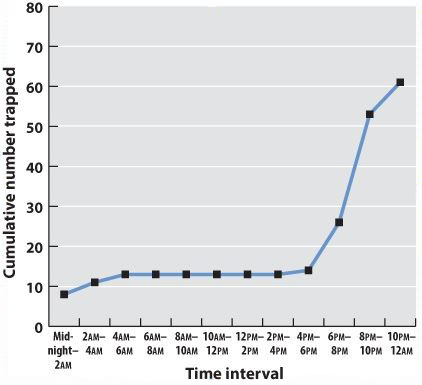
Fig. 3
In science, data are typically presented as a scatterplot, in which points are specified by their (x,y) coordinates. Points are not joined to each other by lines unless there are specified connections among them. Here, plotted in a way similar to the line graph (with the independent variable on the x-axis) is a scatterplot showing the time taken to drive from home to campus for a large number of students. The independent variable is the distance traveled; the dependent variable is travel time because the distances are fixed but travel times vary. Overall, there is a positive correlation between travel time and distance (the further you live from campus, the longer, on average, it will take you to get there), but there is plenty of variation as well. Look at the eight points representing the eight students who live five miles from campus. The variation we see in travel time (from 6 minutes to 30 minutes) is a reflection of differences in driving speed, traffic conditions, and route.
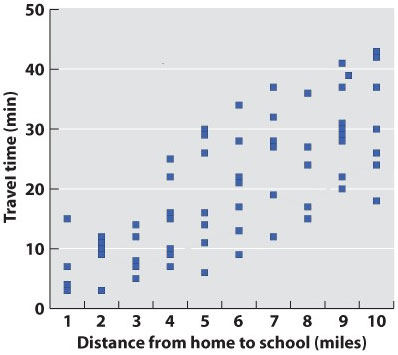
Fig. 4
What if there are more than two variables? Three-dimensional plots can be informative (but can also cause the reader headaches). A popular modern solution to this problem is a so-called temperature plot, in which the third dimension is represented in two dimensions through color: red (hot) for a strong effect in the third dimension and blue (cool) for a weak effect.
Graphs are the mainstay of scientific presentation, but you will see many other ways of presenting data in your textbook. For example, studies showing how different genes interact with each other in the course of development are often illustrated using network diagrams that give the reader a direct sense of the “connectedness” of a particular gene (or node). Evolutionary trees reveal the branching pattern of evolution with species that are closely related having a more recent common ancestor than those that are more distantly related.
Methods of presenting data in science are not limited, even in textbooks, by standard approaches. The popular press has developed many graphics-intense ways of presenting data. Think of an electoral map after an election. You can view information on a number of levels: whether the state is red or blue, the name of the election winner, the size of his or her majority, and so on. Scientists are learning that they too can package information in ways that are simultaneously informative and attractive.
Question
Which of the traits in the bar graph in the previous question is determined mainly by environment?
| A. |
| B. |
| C. |
| D. |
| E. |