Chapter 1. Working With Data 7.12
Working with Data: HOW DO WE KNOW? Fig. 7.12
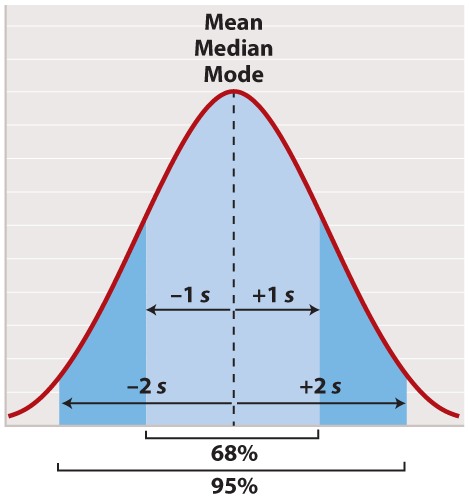
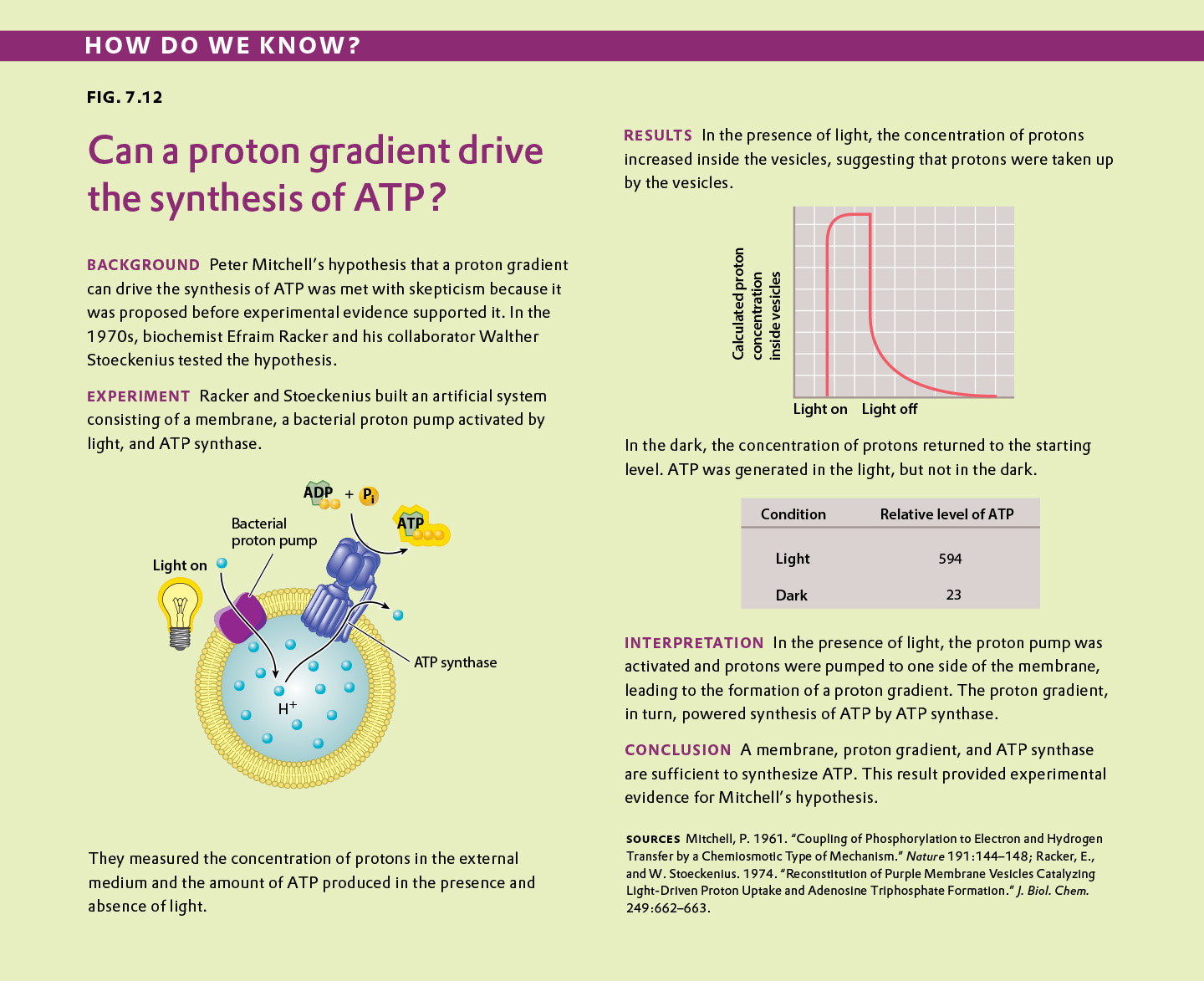
Fig. 7.12 describes experiments linking a proton gradient to the synthesis of ATP. Answer the questions after the figure to give you practice in interpreting data and understanding experimental design. Some of the questions refer to concepts that are explained in the following three brief data analysis primers from a set of four available on Launchpad:
- Experimental Design
- Statistics
- Scale and Approximation
You can find these primers by clicking on “Experiments and Data Analysis” in your LaunchPad menu. Click on “Primer Section” to read the relevant section from these primers. Click on “Key Terms” to see pop-up definitions.
Question
The hypothesis for the experiment described in Figure 7.12 is that:
| A. |
| B. |
| C. |
| D. |
| E. |
| hypothesis | A tentative explanation for one or more observations that makes predictions that can be tested by experiments or additional observations. |
Experimental Design
Types of Hypotheses
A hypothesis, as we saw in Chapter 1, is a tentative answer to the question, an expectation of what the results might be. This might at first seem counterintuitive. Science, after all, is supposed to be unbiased, so why should you expect any particular result at all? The answer is that it helps to organize the experimental setup and interpretation of the data.
Let’s consider a simple example. We design a new medicine and hypothesize that it can be used to treat headaches. This hypothesis is not just a hunch—it is based on previous observations or experiments. For example, we might observe that the chemical structure of the medicine is similar to other drugs that we already know are used to treat headaches. If we went into the experiment with no expectation at all, it would be unclear what to measure.
A hypothesis is considered tentative because we don’t know what the answer is. The answer has to wait until we conduct the experiment and look at the data. When an experiment predicts a specific effect, as in the case of the new medicine, it is typical to also state a null hypothesis, which predicts no effect. Hypotheses are never proven, but it is possible based on statistical analysis to reject a hypothesis. When a null hypothesis is rejected, the hypothesis gains support.
Sometimes, we formulate several alternative hypotheses to answer a single question. This may be the case when researchers consider different explanations of their data. Let’s say for example that we discover a protein that represses the expression of a gene. Our question might be: How does the protein repress the expression of the gene? In this case, we might come up with several models—the protein might block transcription, it might block translation, or it might interfere with the function of the protein product of the gene. Each of these models is an alternative hypothesis, one or more of which might be correct.