Chapter 1. Scientific Measurements
Discussion
Objectives

- Explore: Practice using laboratory balances and glassware to understand the uses and limitations of each and be able to choose appropriate lab equipment.
- Explain: Analyze the results and explain variation in measurements by using the concepts of precision and accuracy, significant figures, and determinate and indeterminate errors.
- Apply: Be able to justify your choice of different laboratory resources, like glassware and balances, for use in future experiments.
Introduction
Two chemistry students are in a heated argument. Pete feels that “scientific experiments are done in a controlled manner and are reproducible if done correctly. Science cannot progress if measurements give different results every time.” But Claire responds that “scientists should take multiple measurements. Results are not always the same and it is wrong to simply perform one test and report the answer.”
Who do you think is right? If measured values are always the same, then why take more than one measurement? If measured values are different, does that mean that science is not reproducible? Or are “true” values never truly known? In this experiment, you will learn more about scientific measurements by investigating the density of water at room temperature and (perhaps) resolve this dilemma. In this process you will also gain familiarity and proficiency with several important laboratory resources, including laboratory glassware and balances.
Solubility is an important topic in chemistry. It has been introduced previously, here we come back to the idea, and later in this course we will talk about it again. Solubility is fundamental to many life processes and a solid understanding is necessary for scientists, health professionals, and engineers alike. Solubility is a physical property that may be quantified. Through daily experiences we know that some things can become more or less soluble if we change the surrounding conditions. If you like to sweeten your tea you know that sugar will dissolve much more easily in hot tea than it will in iced tea. In this lab we will consider some factors that affect solubility.
Table 1.1 Summary of properties measured in this experiment.
| Property | What is Being Measured? |
How Is It Measured? | Additional Information |
|---|---|---|---|
| Mass | The amount of matter in a sample. | Top-loading balance Analytical balance | Common units are grams (g) and milligrams (mg).
Our top-loading balance has a maximum load of 610 g and a precision of 0.01 g. The analytical balance has a smaller maximum load (120 g) and is used for more careful measurements; the precision is 0.0001 g. |
| Volume | The amount of space an object occupies. | Measuring the dimensions of a solid (e.g., with a ruler).
Water displacement for irregularly shaped solids. Liquids are measured in glassware. |
Common units are cubic centimeters (cm3), liters (L), and milliliters (mL). By definition, 1 L = 1000 mL = 1000 cm3.
For precise measurements, burets and pipets are used. Graduated cylinders and beakers are useful when a careful measurement is not necessary. |
| Temperature | The average kinetic energy of the particles (atoms, molecules)comprising matter. | Thermometer | When something becomes warmer, the kinetic energy of its submicroscopic particles increases. As it cools, the kinetic energy decreases. For nearly all materials, an increase in temperature (and hence motion) causes the material to expand.
The temperature tells how warm or cold an object is relative to a standard. In the lab we report temperature on the Celsius (°C) or Kelvin (K)scales. |
| Density | The ratio of an object's mass to its volume. | Calculated from mass and volume data. | Usually reported in g/cm3 or g/mL. |
Reading Scale Values
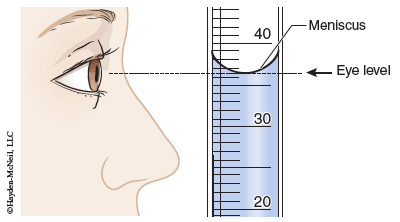
The volume of a liquid is measured in graduated glassware by recording the position of the bottom of the meniscus (the curved surface of a liquid in a tube). As shown in the fi gure, it is important to place your eye perpendicular to the glassware to obtain a correct reading. In this example a reading of 36.5 mL is appropriate. When reading a scale value, the number you should record include all of the digits that are known, plus one that is estimated. In this example, the bottom of the meniscus is clearly greater than 36.0 and less than 37.0; a reasonable estimate is 36.5 mL. Graduated laboratory glassware such as burets or graduated cylinders, as well as thermometers, are read in this manner.
Calculations
Dimensional analysis is a common problem-solving approach and in this experiment it can be used for density calculations. Conversion factors are used to ensure that the answers to problems are in the correct units. In this method both the numbers and the units are multiplied together, divided into each other, or canceled out. The end result will be a number and a unit.
Example: A student weighed a marble to obtain a mass of 4352.4 mg and measured a volume, by displacement, of 2.31 mL. What is the density in g/cm3 of the marble?
The question is asking for density, which is mass divided by volume, in units of g/cm3. The measurements give us the mass and volume, but not in the units we need. We can use conversion factors with dimensional analysis to solve this problem:
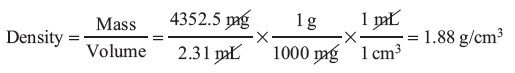
Question 1.1: The student then decided to cool the same marble and see if the density changed. After analysis, the density of the colder marble was determined to be 1.91 g/cm3. What are the mass and volume of the cold marble?
Experimental Measurements
Precision and accuracy are commonly mentioned in discussions of experimental measurements. Precision refers to how closely individual measurements agree with one another and accuracy refers to how closely a measured value agrees with the accepted value.
Question 1.2: A chemist analyzed a liquid sample multiple times by two different
methods. The sample has an accepted density of 0.9855 g/mL.
| Measurement # | Method A | Method B |
|---|---|---|
|
1 2 3 4 |
0.9834 0.9844 0.9838 0.9843 |
0.9855 0.9754 0.9847 0.9799 |
Which method has better precision?
Which method has better accuracy?
The chemist decided that Method A was better than Method B (do you agree?) and reported an average value of 0.983975 g/mL. This may seem like a good idea, but clearly their laboratory equipment can only determine the density to the 0.0001 place. It does not make sense to report an average value 0.983975 g/mL because it implies a much more precise measurement than the one possible with the available equipment. It would be possible to determine a density value to this level of precision, but it would require more sophisticated (and expensive) laboratory resources.
It is important to properly use laboratory resources to obtain and report the maximum number of significant figures, which are the digits that indicate the precision with which a measurement is made. For example, a mass reading on an analytical balance of 12.0409 g has six significant figures. Measuring the same object on a top-loading balance would result in only four significant figures. You should be able to explain this based on the precision of the instruments as listed in the table above. Your textbook has more information on the calculation of significant figures.
It should be recognized that the reported number of significant digits encompasses all measurements in a given procedure. Often, a single piece of glassware or instrumentation will limit the number of significant digits that can be obtained.
Returning to the above example, you will notice with Method A 1) the measured density value is consistently less than the accepted value, and 2) repeated measurements produced different density values. The idea of errors in measurement may be used to describe both of these.
Errors in measurement fall into two categories: determinate errors and indeterminate errors. A determinate error is one that has an identifiable source and can be corrected for. Examples of determinate errors include using a meter stick that is actually 1.020 meters long or reading the top of the meniscus instead of the bottom. Both of these errors can be identified and corrected. Note that determinate errors will have a directional bias. Using a “meter” stick that is 1.020 meters long will always result in an error that understates the actual length. It is likely that Method A has a determinate error that leads to a result consistently less than the accepted value.
Indeterminate errors are those that cannot be identified and corrected. For example, in our effort to obtain the maximum number of significant figures we estimate the last digit when reading a scale value. Sometimes the estimate might be too high, other times too low. In either event, it is not possible to estimate the last value in a reproducible way every time. This results in unavoidable variation in the reported value. Even when a value is recorded from a digital instrument (like with a pH meter or analytical balance), there is unavoidable uncertainty in the last digit. This means that, even if determinate errors are absent and the procedure followed flawlessly, there will be indeterminate errors that lead to variation in the measured values. Indeterminate errors will always lead to a range of measured values, and they will not display the directional bias of a determinate error. If only indeterminate error is present, taking multiple measurements and averaging the results is a good way to approximate the true value. The fact that Method A did not always provide the same measured value is consistent with the unavoidable presence of indeterminate errors.
Finally, please note that a scientist’s treatment of error differs from how others view error. For a scientist, “error” is not forgetting to close the door or writing down the wrong number; if these mistakes occur, the experiment should be started over! Instead, errors are an inevitable part of measurement. To have the very best precision and accuracy it is important to identify and remove determinate errors and reduce the magnitude of indeterminate errors.
Experimental Design (Procedure)
In this experiment, your task is to prepare plots of mass/volume for distilled water at room temperature using four different pieces of laboratory glassware. Each mass/volume plot should have at least four different measured values that are between 5 mL and 25 mL (see the following figure). The mass will be measured with a laboratory balance.
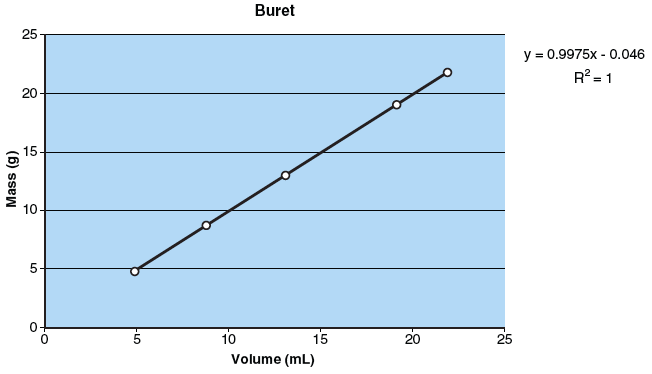
- At the start of the experiment, the teaching assistant may demonstate the correct use of the 25 mL buret, the graduated cylinder, the pipet, and the beaker. They will also communicate the correct operation of the laboratory balance and thermometer.
- As mentioned above, a liquid's density will be affected by temperature. Impurities in a liquid may also affect the density. For these reasons, begin the experiment by adding distilled water to a 250 mL beaker and letting it reach room temperature. To avoid repeating this step, add ~200 mL of distilled water. You will use this water in subsequent steps.
- Use a laboratory balance to determine and record the mass of a 100 mL beaker. This is the "weighing beaker." Remember to tare the balance before the measurement. In your notebook, record all digits; they are all significant.
- Fill the 25 mL buret with the water from step 2, following the instructions you received in the demonstration. Transfer at least 5 mL of water to the weighing beaker. Record the temperature of the water and record the exact amount transferred. Record the appropriate number of significant figures (see discussion above on reading scale values). Liquid must not be transferred in the balance room.
- Return to the balance room and record the new mass of the weighing beaker with water. Use the same balance for steps 3 and 5, remembering to tare the balance before each measurement.
- Repeat this procedure until you have four different values that are between 5 mL and 25 mL for the buret.
- Move on to the next piece of glassware and repeat steps 3 through 6. After finishing with the buret, you should move on to graduated cylinder, then the pipet, and finally the beaker.
Glassware to use:

Balances available in lab:

Materials Provided
Equipment
- 2-100 mL beakers (~50 g each)
- 1-250 mL beaker (~110 g)
- 1-400 mL beaker (~136 g)
- 1-600 mL beaker (~172 g)
- 2-125 mL Erlenmeyer flasks (~82 g each)
- 3-250 mL Erlenmeyer flasks (~120 g)
- 1-25 mL buret and buret clamp
- 1-10 mL graduated cylinder
- 1-100 mL graduate cylinder
- 1-5 mL volumetric pipet
- 1-10 mL volumetric pipet
- rubber pipet bulb
- 1-thermometer (–20°C–100°C)
Common Equipment
- top-loading balances
- analytical balances
- Parafilm (covers glassware)
Chemicals
- none
Cautions
Goggles must be worn in the laboratory.
Procedure
You are responsible for recording your procedure in your notebook. You should provide a sufficient level of detail such that another scientists could repeat your experiment.
Waste Disposal
All solutions may be rinsed down the drain.
Data (Use the correct number of significant figures)
Water temperature: ______________
Water, accepted density at room temperature (calculated): ____________
At 4°C water’s density is 1.000 g/cm3. For the range of temperatures associated with “room temperature” (from about 20°C to 30°C), the density of pure water is:
Density (g/cm3) = [–0.00030 (g/°C · cm3) Temperature (°C)] + 1.0042 (g/cm3)
| Glassware | Mass of Water (g) | Volume of Water (mL) | Measured Density (g/mL) | Actual Density (g/mL) | Error1 | % Error |
|---|---|---|---|---|---|---|
| Buret | ||||||
| Buret | ||||||
| Buret | ||||||
| Buret | ||||||
| Graduated Cylinder |
||||||
| Graduated Cylinder |
||||||
| Graduated Cylinder |
||||||
| Graduated Cylinder |
||||||
| Pipet | 5.00 | |||||
| Pipet | 10.00 | |||||
| Pipet | 15.00 | |||||
| Pipet | 20.00 | |||||
| Beaker | ||||||
| Beaker | ||||||
| Beaker | ||||||
| Beaker |
1 Error = experimental value – true value.
The relative error = error/true value.
The % error = relative error X 100%.
Report Details
Answer the following questions.
- A discussion of precision and accuracy is included in this experiment. Use these terms to rank the precision and accuracy of each type of glassware tested. Support your analysis with your data.
- What does the slope of each mass/volume plot represent? What information does the plot provide that a single measurement does not? What would the plot look like if a determinate error were present?
- A mass/volume plot includes two measured properties (mass and volume) and one calculated property (density). How does the plot illustrate the intensive or extensive nature of each of these properties?
Answer Clinic
Scientific Measurements
Question 1.1: A student analyzed a marble to obtain a mass of 4352.4 mg and measured a volume, by displacement, of 4.31 mL. The resulting density was 1.88 g/cm3. The student then decided to cool the same marble and see if the density changed. After analysis, the density of the colder marble was determined to be 1.91 g/cm3. What are the mass and volume of the cold marble?
Answer The density = 1.91 g/cm3. This is a ratio of mass/volume. In the original question the mass = 4352.4mg and the volume = 2.31 mL. With a change in temperature will the mass change or the volume? It must be the volume because the amout of matter in the marble has not changed, only the amount of space it takes up.
Mass = 4352.4 mg

Question 1.2: A chemist analyzed a liquid sample multiple times by two different methods. The sample has a true density of 0.9855 g/mL.
Measurement # Method A Method B 1 0.9834 0.9855 2 0.9844 0.9754 3 0.9838 0.9847 4 0.9843 0.9799
| Measurement # | Method A | Method B |
|---|---|---|
| 1 | 0.9834 | 0.9855 |
| 2 | 0.9844 | 0.9754 |
| 3 | 0.9838 | 0.9847 |
| 4 | 0.9843 | 0.9799 |
Which method has better precision?
Answer The range of values for method A is much narrower. Method A has better precision. Which method has better accuracy?
Answer
The true value = 0.9855.
The average for method A = 0.9840. The average for method B = 0.9814
Method A has better accuracy. Note: It is difficult to determine the accuracy if the precision is poor as the results will be widely scattered. Simply calculating an average may be misleading under these circumstances.
Activity Completed!
Activity results are being submitted...