Chapter 1. Freezing Point Depression
Objectives

- Use laboratory techniques to explore the freezing point depression of a solution.
- Determine the molecular weight of an unknown compound by measuring the freezing point depression.
Introduction
Freezing point depression is an interesting property of solutions. We routinely exploit this phenomenon in clever ways. If you have made your own ice cream before then you have experimented with freezing point depression. Water will freeze to ice at 32°F. In order to freeze the components that make up ice cream, the temperature must be lower than this. We can add salt to our water/ice mixture and this lowers the freezing point, low enough to freeze ice cream. Living in Ohio we see city trucks laying salt and brine solutions on the roads; the purpose is again to lower the freezing point of water, so that ice formation on the roads is reduced. In this lab you will determine the freezing point of a pure liquid, and then again for a solution. Using the freezing point depression you will be able to calculate the molecular weight of the unknown solute.
Connection to Lecture
When the temperature of a liquid is decreased, the average kinetic energy of the particles (molecules, ions, or atoms) decreases. With the reduced motion of the particles, intermolecular forces can take over and hold the particles in a fixed array—the liquid freezes. The temperature at which this occurs is the freezing point and it is characteristic of each pure substance.
If we raise the temperature of a solid, the kinetic energy and molecular motion increase until the particles have energy to overcome forces of attraction holding the solid state—the solid melts. The temperature at which this happens is the melting point and it is the same temperature as the freezing point. Melting point and freezing point are both best defined as the temperature at which solid and liquid exist in equilibrium.
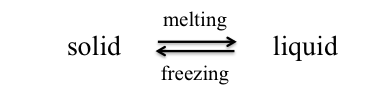

Freezing Point Depression and This Lab
Now consider adding a second substance that is soluble in the liquid and forms a solution with the original liquid as solvent.

The equation represents the usual case: the solid that freezes from a solution is pure solvent. The temperature at which this equilibrium is established (the freezing point of the solution) is lower than the freezing point of pure solvent. The explanation is that the solute interferes with the freezing process but does not affect the melting process. When solute is present, some of the positions in the solution at the surface of the solid are occupied by solute, so less solvent particles are available to become attached to the surface. The presence of solute particles next to the surface does not affect particles moving from solid to liquid. More melting occurs in a given amount of time than freezing and the solid melts. Decreasing the temperature favors the freezing process and re-establishes equilibrium.
The difference in temperature between the freezing point of pure solvent and the solution is the freezing point depression, ∆Tf. The freezing point depression depends on the amount of interference by solute in the freezing process, which is directly proportional to concentration of solute particles. The quantitative relationship for a non-dissociating solute is
where Kf is the freezing point depression constant in °C/m, and m is the molal concentration.
Question 15.1: What are the units of m, molal?
The value of Kf is different for each solvent. It is an experimentally determined proportionality constant between freezing point depression and molal concentration.
In this experiment we are using freezing point depression to determine the molality of a solution and then the molecular weight of the solute. Two factors limit the application of this method for determining molecular weights. One is the fact that the equation only applies to dilute solutions; the relationship becomes nonlinear at higher concentrations. The other limiting factor is solubility. Low solubility leads to a very small observed freezing point depression.
The literature value for the freezing point (melting point) of cyclohexane is 6.5°C. The value that you measure will probably be somewhat different due to slight impurities in the cyclohexane and the calibration of the thermometer. These factors will have no net effect on your final value since the freezing point depression is determined by difference.
For pure cyclohexane, the same temperature should be observed any time some of both solid and liquid are present and the system is at equilibrium. The cyclohexane solutions are prepared with known amounts of solute and liquid solvent. As solvent freezes out of the solution, the concentration of the solution increases and the freezing point decreases. We therefore need to record the temperature when the first crystal appears or the last crystal melts so that the concentration of the solution is known. For cyclohexane solutions, more reproducible results are obtained by observation of the melting process. The solution is cooled until crystals form, and then allowed to warm slowly. For practice, record the temperature at which the last crystal melts for the pure cyclohexane also. Each determination of the melting point is repeated until consistent values are recorded.
Data Analysis
The freezing point depression, ΔTf, is the difference between the freezing point (f.p.) of the pure solvent and the freezing point of the solution.
Question 15.2: Will the ΔTf be a positive or negative value? Why?
The freezing point depression constant, Kf, for cyclohexane is 20.00°C/m; molality can be calculated from:
Molality, m, is defined as
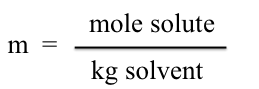
To calculate moles of solute present, we need to know how many kilograms of solvent were used. The density of cyclohexane is 0.799 g/mL. If 20.00 mL of cyclohexane is used, the calculation is
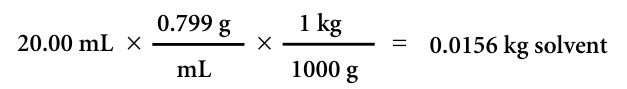
Note: Substitute the volume you used if it was not 20.00 mL. Now the moles of solute may be calculated:
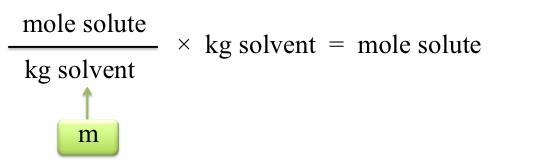
Since our sample was initially weighed we have the g of solute, and with the moles determined we may then calculate the molecular weight of the sample. (The molecular weights should not differ by more than 5%.)
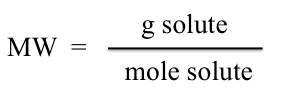
Materials Required
Equipment
- 25-mL buret
- ring stand, clamp
- 100-mL beaker
- micropipet, rubber hose
- ice bath (400-mL beaker)
- freezing point apparatus
- digital thermometer
Chemicals
- acetone
- cyclohexane
- unknown sample
- rock salt
- ice
Common Equipment
- analytical balance
- water aspirator
Cautions
Cyclohexane is a skin irritant. Wash any affected area with soap and water. Goggles must be worn at all times.
Procedure
Answer questions in your lab notebook as you go along. Discussions with your peers and TA are encouraged.
- Obtain a freezing point apparatus from your lab instructor. Check out a digital thermometer display and probe from the storeroom window (Student ID required).
- Clean the smaller, sample test tube with soap and water. Shake out most of the water and rinse the tube with 5 mL of acetone. Collect the acetone in a small beaker for disposal. Connect a rubber hose to a working aspirator (position the stopper in the drain and turn on the water). Connect a micropipet to the hose and insert the micropipet into the test tube to completely dry the test tube. If necessary, repeat the acetone rinse and aspirator procedure until the tube is dry.
Question 15.3: Why is it important that the tube be dry? - Clean a buret with soap and water. Drain out the water and rinse the buret with 5 mL of acetone. Collect the acetone in a small beaker for disposal. Connect a rubber hose to a working aspirator and connect the hose to the tip of the buret to completely dry the buret. If necessary, repeat the acetone rinse and aspirator procedure until the buret is dry.
- Rinse the buret with 5 mL of cyclohexane and collect the cyclohexane for disposal. Fill the buret with cyclohexane. Measure about 20 mL of cyclohexane, to the nearest 0.01 mL, into the clean, dry sample test tube. Record the initial and final volumes from the buret.
- Insert the thermometer and stirring wire into the test tube. (Note the temperature – it should be close to room temperature at the start.)
- Put the sample test tube into a 400 mL beaker containing an ice/salt water bath. Periodically stir the cyclohexane with the stirring wire while it is cooling. When the cyclohexane has partially frozen, remove the test tube from the water bath. Completely dry the outside of the test tube.
- Place the sample test tube into the larger test tube, which will serve as an air jacket. Gently stir the contents of the test tube while the solid cyclohexane melts. Record the temperature to the nearest 0.1°C when the last bit of solid cyclohexane melts.
- Repeat steps 6 and 7 until three determinations are within close agreement (typically within 0.1°C). Record all determinations in your lab notebook. The average of your three determinations will be recorded as the melting point of pure cyclohexane on your lab report form.
- Obtain a clean sample of an unknown organic solid from your lab instructor.
- Weigh a clean, dry weighing dish on an analytical balance. Add 0.3 g of your unknown to the dish. Weigh the dish with the sample to the nearest 0.0001 g. Carefully add the sample to the test tube containing the cyclohexane. Do not leave any solid on the walls of the test tube; all of the sample must be dissolved. Reweigh the empty dish to the nearest 0.0001 g.
Question 15.4: Why is it important to dissolve all of the added solid? - Put the sample test tube into a 400-mL beaker containing an ice/salt water bath. Periodically stir the solution with the stirring wire while it is cooling. When the cyclohexane has partially frozen, remove the test tube from the water bath and completely dry the outside of the test tube.
- Place the sample test tube into the larger test tube, which will serve as an air jacket. Gently stir the solution while the solid unknown melts. Record the temperature to the nearest 0.1°C when the last bit of solid cyclohexane melts.
- Repeat steps 11 and 12 until all three determinations are within close agreement (typically within 0.1°C). Record all determinations in your lab notebook. The average of your three determinations will be recorded as the melting point (freezing point) of the solution (Trial 1) on your lab report form.
- Repeat steps 10 through 13 twice using additional sample weights of 0.2 g and 0.1 g for Trials 2 and 3. Note that the weights are cumulative so that the molality will increase causing the freezing point to decrease.
- Collect the cyclohexane solution in your waste beaker and return the freezing point apparatus.
Waste Disposal
The acetone, cyclohexane, and unused unknown must be collected in the organic waste beaker, and the waste disposal sheet should be properly filled in. Your lab instructor will dispose of the total volume in the appropriate container.
Points to Consider
In this lab you determined the freezing point of a pure liquid and that of a solution.
- Include your completed report sheet with sample calculations.
- Does your reported freezing point depression that was obtained experimentally make sense?
- What were the moles of solute calculated, and the calculated molecular weight?
- Do the molecular weights for each trial agree with each other?
- What are plausible sources of error? How would these impact the molecular weight calculated?