Chapter 14. Determination of Molar Mass and van der Waals’ Constants
Objectives

- Use laboratory techniques to determine the mass, temperature, pressure, and volume of a gaseous sample. Use this information to calculate the molar mass of an unknown sample.
- Calculate the van der Waals’ constants and understand their significance. Be able to explain why intermolecular attractions and molecular volumes cause real gases to deviate from ideal behavior.
Introduction
“How real is a real gas?” This may seem like an odd question. Why should some gases be more “real” than others? And what is the alternative to a gas behaving like a real gas? Chemists often find it helpful to simplify the relationships between several measurable properties that characterize a gas, i.e., its pressure, volume, temperature, and number of moles, by assuming they are related in an “ideal” manner. It turns out that many gases behave quite close to this ideal approximation. Many other gases, however, deviate significantly from the ideal approximation and so they are more “real.” In this experiment you will investigate such a gas, determine its molar mass, and calculate its van der Waals’ constants. These van der Waals’ constants are used to describe how a gas deviates from an ideal one and, in a sense, communicate how real the gas actually is.
Discussion
The Ideal Gas Law
The ideal gas law describes the relationship between the pressure, volume, temperature, and number of moles for a gaseous sample.
In this equation, P is pressure, V is volume, n is number of moles, R is the ideal gas constant, and T is temperature. If these values are expressed in units of atmospheres, liters, moles, and Kelvins, the value of the gas constant is
The hypothetical gas whose behavior conforms to this equation under all conditions is an ideal gas.
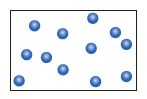
Question 11.1: Consider the sample of gas depicted here. What would the drawing look like if the volume and temperature remained the same but the pressure decreased by a factor of 2?
The number of moles of an ideal gas, n, can be calculated from its mass and molar mass:
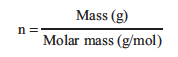
Substituting into the ideal gas equation, we obtain:
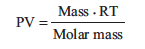
Then rearranging to solve for the molar mass we get:
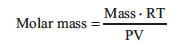
By determining the mass, temperature, pressure, and volume of a particular gas sample, it is possible to calculate the molar mass.
Question 12.2: Calculate the molar mass of a gas if 2.50 g occupies 0.875 L at 685 torr and 35 °C.
Non-Ideal Gas Behavior
Another definition of an ideal gas is a gas whose behavior conforms to all postulates of the kinetic molecular theory under all conditions. Your sample in this investigation is a very real gas, having properties that differ from those of an ideal gas.
One of the postulates of the kinetic molecular theory states: The volume occupied by thegas particles is extremely small compared to the space between them. The particles are treated as points. The atoms or molecules of a real gas do have a finite volume, so the volume in which the particles are free to move, Videal, is less than the volume of the flask that was measured, Vmeas, by the volume occupied by the particles, nb,
where n is number of moles of gas and b is the molar volume of the particles, the volume occupied by one mole, L/mol. The molar volume can be estimated from the density of the liquid and molar mass. In a liquid, there is very little empty space so the volume occupied by the liquid is the volume occupied by a large number of particles. Molar volume is approximated by

Notice that the density, given in g/mL, has been converted to g/L.
Another postulate of the kinetic molecular theory states: Intermolecular forces of attractionbetween particles of the gas are negligible. The fact that our gas samples are so easily condensed to liquid indicates non-ideal behavior. It is the forces of attraction between particles that hold the liquid state and so a hypothetical ideal gas, which has not attractive forces, could not be liquefied.
For a real gas, the intermolecular forces of attraction require a correction on the pressure term in the ideal gas law expression. Why is the pressure affected by intermolecular attractions? What we observe as pressure is the result of collisions of the particles with the walls of the container. Consider Figure 12.1, in which a particular gas molecule (the darkened circle) is traveling toward the wall, about to collide and exert a pressure.
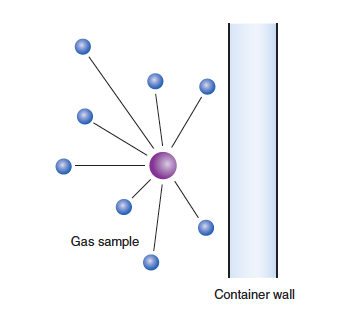
However, this particular gas molecule is attracted to other molecules in the sample (blue circles), and these attractions are mostly in a direction away from the wall. The result is that when the molecule hits the wall, the collision will be less forceful and the pressure will be less than ideal. A correction term must be added to the measured pressure:

The constant, a, reflects the strength of intermolecular forces, a larger value indicating stronger forces of attraction. The factor n2/V2 is a concentration term, reflecting the fact that a large number of molecules in a smaller volume will have a greater attraction.
Substituting both the corrected pressure and volume terms into the ideal gas equation, we obtain the van der Waals’ equation for a non-ideal gas:
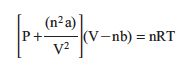
Question 12.3: Which statement is true for a non-ideal gas?
- In the van der Waals’ equation, the “a” value is small.
- In the van der Waals’ equation, the “b” value is small.
- The volume of the gas molecules is relatively large.
- There is no force of attraction between gas molecules.
Analyzing Your Data
The procedure has two parts:
A. Determine the mass, temperature, and pressure of the gaseous sample.
B. Determine the volume of the sample.
The unknown sample is a liquid at room temperature, and vaporizes when heated. The gas sample will be contained in a modified flask like that shown in Figure 12.2. A small amount of liquid is placed in the flask and heated in a hot water bath until all of the liquid vaporizes. This process forces the air out and fills the flask with vapor. Note the glass tip has a small capillary bore. Vapor will escape through the capillary pushing out air. When the sample has completely vaporized, exchange of vapor and air is extremely slow.
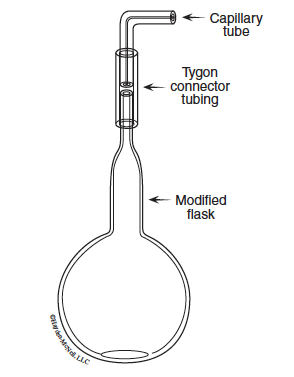
The gas sample (vapor) now occupies the entire volume of the flask at the temperature of the water bath and at atmospheric pressure. The flask containing the vapor is removed from the bath and allowed to cool, causing condensation of the sample. The mass of the sample is determined by subtracting the mass of the empty flask from the mass of the flask containing the recondensed sample. Temperature of the gaseous sample is determined by measuring the temperature of the water bath; pressure is atmospheric pressure.
Use the equation
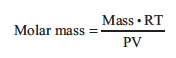
to estimate the molar mass of your unknown. The mass, m, is the mass of recondensed liquid. The gas constant, R, equals 0.08206 L · atm · mol–1· K–1. Temperature, T, is the temperature of water in the water bath in Kelvins. The pressure, P, is atmospheric pressure in atm. The volume of the flask, V, is calculated from mass and density of water.
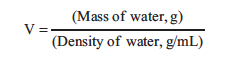
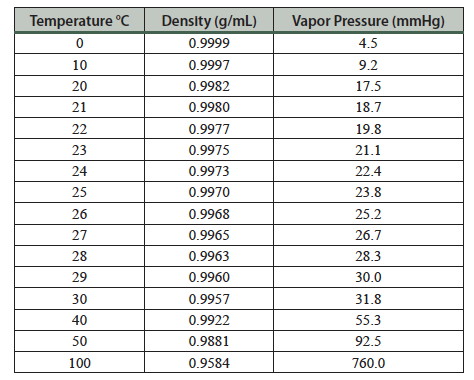
The density of water used to fill the flask should be found in Table 12.1, since it varies with temperature. Convert the volume to liters.
When you receive your unknown sample, you will be provided with an elemental analysis and density of the liquid. Use the analysis to calculate the empirical formula of your unknown sample. Divide the experimental molar mass by the empirical formula weight to determine the molecular formula. Round the ratio down to the nearest whole number. Calculate the actual molar mass from this formula.
The calculation of the experimental molar mass assumes ideal behavior for the gas sample. We can get an indication of non-ideality (“How non-ideal is it?”) by using experimental values for m, T, P, and V, with the actual molar mass, to calculate an “experimental” R.
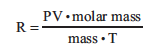
The percent error for R is then calculated.
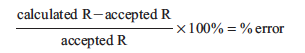
Any experimental error also shows up in R using this calculation. Calculate R and the % error for all three trials. Use the trial that gives the lowest % error for Part E of the Report Sheet.
Now determine the van der Waals’ constants for your gas. First calculate b from liquid density.

Finally, use the van der Waals’ equation to calculate the constant a. For number of moles, n, use the experimental mass of unknown and the actual molar mass.
Question 12.4: Cyanogen is a toxic gas that is 46.2% C and 53.8% N by mass. At 25 °C and 751 torr, 1.05 g of cyanogen occupies 0.500 L. What is the molecular formula of cyanogen?
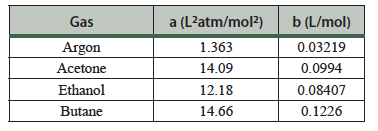
Question 12.5: Based on their van der Waals’ constants, which gas deviates most from being an ideal gas?
Materials Required
Equipment
- modified flask (volume ~260 mL)
- medicine dropper
- clamp, ring stand
- thermometer
- rubber tubing
Chemicals
- acetone, C3H6O
- unknown sample
- barometer
- rubber tubing
- top-loading balance
Common Equipment
- water bath, hot plate
- micropipet
- water aspirator
- analytical balance
Cautions
Be careful to avoid burns from the hot plate. The organic unknown samples have flammable vapors so all heating is done in the large hoods. The fume hoods should also be on.
Procedure
All weighings should be done without the capillary tip.
- Rinse out the modified flask with 5 mL of acetone. Collect the waste acetone in a beaker at your desk. Dry the flask with a micropipet connected to the water aspirator. (See Figure 12.3.)
- Weigh the empty, dry flask on the analytical balance. Use a medicine dropper to add 5 mL of your unknown liquid to the flask. Attach the capillary tip with the Tygon tubing. The tubing should be evenly distributed on both glass pieces, which should be tightly held together.
- Attach a clamp to the neck of the flask to hold it while in the water bath. However, the flask should be held in a towel in your hand when transporting it around the lab room. Completely submerge the flask in a water trough provided by your lab instructor. The water trough is heated on a hot plate in a large hood due to the vaporization of flammable organic liquids.
- Heat the flask until the liquid is completely vaporized. Often liquid will form in the capillary tip. When the liquid is gone, record the temperature in the trough and remove the flask. Allow the flask to cool with the tip on. Read the pressure from the barometer in the balance room. This is the pressure of your gas sample.
- Upon cooling, the gaseous sample will re-liquefy. After the flask has been cooled somewhat, it can be cooled further by running cold tap water over it.
- Dry the outside of the flask, remove the tip by carefully pushing the Tygon tubing off the flask (like a champagne cork), and weigh the flask. If the weight appears to increase while the flask is on the balance, cool it further and reweigh the flask.
- Repeat steps 2 through 6 two more times. It is not necessary to clean, dry, and reweigh the flask prior to adding more unknown.
- Rinse out the modified flask with 5 mL of acetone. Collect the waste acetone in a beaker at your desk. Dry the flask with a micropipet connected to the water aspirator.
- Weigh the empty, dry flask on the top-loading balance.
- Fill the flask with distilled water from a wash bottle. Weigh the flask and water. Determine the temperature of the water. The density of water can be obtained from this table.
Table 12.1 Density of water at varying temperature and pressure.
- Empty the flask using a micropipet connected to the water aspirator. Hold the flask upside down, and insert the micropipet. (See Figure 12.4.)
- Repeat steps 10 and 11.
- Repeat step 8 and return the clean, dry flask to your lab instructor.
- Get the data sheet from your lab instructor, which includes the elemental analysis and liquid density for your unknown.
Waste Disposal
Acetone and your leftover unknown must be disposed in the organic solvents waste beaker, and the waste disposal sheet should be properly filled in. Your lab instructor will dispose of the total volume in the appropriate container.