Chapter 16. Vapor Pressure and the Heat of Vaporization

Objectives

Laboratory 14

false

Use experimental techniques to record temperature and volume data for known and unknown compounds in which the liquid and gas are in equilibrium, and determine the boiling point of the liquid.
Utilize the Clausius-Clapeyron equation to calculate the heat of vaporization.

Introduction

The boiling of a liquid is a common phenomenon familiar to all of us. In both the kitchen and the laboratory we have all observed the boiling of water. We have also observed what happens when a puddle of water evaporates on a sunny day. In these examples the water molecules become gaseous, leave the system (the water) and enter the air (the surroundings). Would the boiling of water, or any other liquid for that matter, be affected if the gaseous molecules remained part of the system? What happens if the liquid and the gas above it are a closed system, i.e., a system in which energy can be exchanged with the surroundings but matter cannot? In this laboratory experiment you bring together the concepts of intermolecular forces, boiling point, and vapor pressure and develop a model to be able to answer questions like these.

Discussion

Molecules can escape from the surface of a liquid into the gas phase by evaporation. In order to escape the liquid the molecule must overcome the intermolecular forces that attract it to other molecules in the liquid phase. If a liquid is heated the motion of the molecules increases. With this increase in kinetic energy some molecules have sufficient energy to overcome the attractive forces holding it in the liquid phase. The amount of energy required to vaporize a mole of liquid is the heat of vaporization, ΔH_vap. The units for heat of vaporization are generally kJ · mol^–1:

H₂(l) → H₂O(g) ΔH_vap = 40.7 kJ · mol^-1

Question 14.1: Which statement(s) regarding the heat of vaporization is/are true?

The heat of vaporization is always a positive number because energy is required to overcome the intermolecular forces that are holding the molecules in the liquid phase.
The heat of vaporization may be positive or negative depending on the particular intermolecular forces present in the liquid phase.
A strong intermolecular force corresponds to a small heat of vaporization.

What happens after the particles enter the gas phase? If the vessel is open to the atmosphere they may disperse and move away from the liquid. However, if they happen to strike the surface of the liquid they can be recaptured and return to the liquid phase. Obviously, as the concentration of gas-phase molecules increases the probability that they will strike the surface and condense, i.e., go from the gas phase to the liquid phase, also increases. We therefore have two processes taking place simultaneously; evaporation of the liquid and the condensation of the gas. When two processes occur simultaneously at equal rates, they are said to be in dynamic equilibrium. Even though it may appear nothing is happening, a great deal is happening as some of the molecules continuously pass from liquid to gas state, and from gas to liquid state.

Suppose the evaporation of the liquid and condensation of the gas takes place in a closed system. When the molecules are in the gaseous phase they will exert a pressure as they strike the walls of the container (see Figure 14.1). The vapor pressure of a liquid is the pressure exerted by its vapor when the liquid and vapor are in dynamic equilibrium.

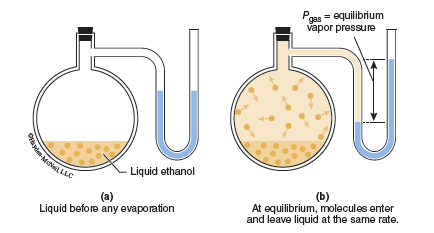
Figure 14.1 Illustration of the equilibrium vapor pressure over a liquid.

In (a) we imagine that no molecules of the liquid are in the gas phase initially; there is zero vapor pressure in the vessel. In (b), after equilibrium is reached, the rate at which molecules leave the surface equals the rate at which gas molecules return to the liquid phase. These equal rates produce a stable vapor pressure that does not change as long as the temperature remains constant. What do you predict happen if there are initially no gas molecules above the liquid (Figure 14.1a)? If there is no external pressure being exerted on the liquid’s surface, it will be easier for the gas molecules to escape into the vapor. In other words, the evaporation of a liquid is affected by the external pressure acting on the liquid surface. When the vapor pressure equals the external pressure acting on the liquid it is boiling. The boiling point of a liquid at 1 atm (760 torr) pressure is called its normal boiling point.

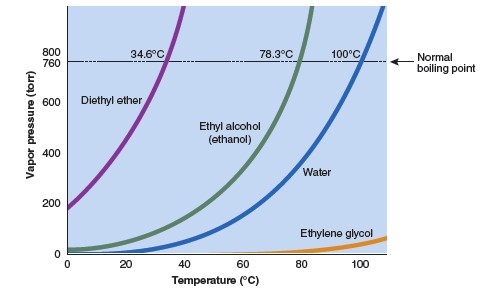
Figure 14.2 Vapor pressure for four common liquids as a function of temperature.

Question 14.2: What do the liquids shown in Figure 14.2 have in common? Select all true statements:

They all have the same vapor pressure at 100 °C.
They all boil at the same temperature.
They all boil at the same vapor pressure.
They all have the same ΔH_vap.
As the temperature increases, the vapor pressure increases.

There is a quantitative relationship between vapor pressure, temperature, and heat of vaporization known as the Clausius-Clapeyron equation,

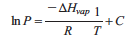
where P is the vapor pressure at temperature T, ΔH_vap is the heat of vaporization, R is the gas constant, 8.315 J · mol⁻¹· K⁻¹, and C is a constant. The units of R makes clear that temperature must be in Kelvins and that ΔH_vap will have units of J · mol⁻¹. Notice that the equation has the form of the equation of a straight line. If the vapor pressure is determined at a number of different temperatures, a graph of ln P vs. 1/T should be a straight line with a slope of −ΔH_vap /R and

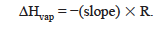
In this way, it is possible to experimentally determine the ΔH_vap and one of the points on the graph will be the boiling point, i.e., the temperature at which the vapor pressure equals atmospheric pressure.

Question 14.3: Which statement correctly states the relationship between intermolecular force, vapor pressure, and normal boiling point?

Analyzing Your Data

The procedure has three parts:

a. Determine temperature–volume data for a known compound.

b. Determine temperature–volume data for an unknown compound.

c. Determine the boiling point of the unknown compound.

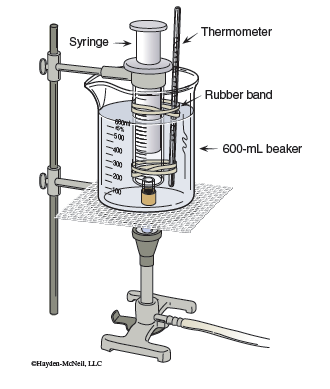
The temperature–volume data is obtained by injecting a small amount of the compound to be studied into a 30-mL syringe. The syringe is immersed in a water bath and the water is slowly heated. The experimental setup is shown in Figure 14.3. Volume readings are taken at five different temperatures.

At each of the five temperatures, the liquid will establish its vapor pressure. The vapor pressure is then calculated from volume measurements using Dalton’s law and the combined gas law. The known compound is one in a set of three related compounds, and data for the other two known compounds in the set will be obtained from students designated by your lab instructor. After the syringe is cleaned and dried, the procedure is repeated with the unknown sample.

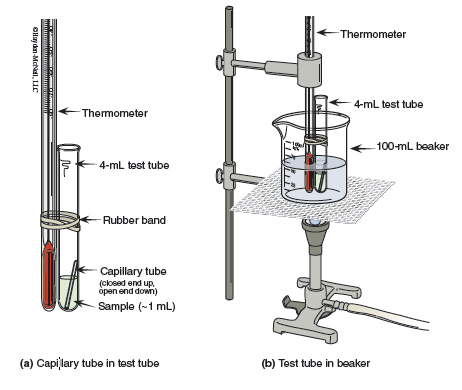
Figure 14.3 Determining temperature–volume data.

In the third part of the experiment the boiling point of the unknown sample will be determined. The setup for the boiling point determination is shown in Figure 14.4. The key to a successful boiling point determination is to keep everything on small scale: A 100-mL beaker is used for the water bath; a 4-mL test tube contains 1 mL of the sample. A capillary tube is broken to a length of approximately 3 cm and placed, open end down, in the liquid. As the temperature is slowly increased, a fine stream of bubbles will come from the capillary tube as vapor from the unknown liquid forces air from the capillary tube. After a few seconds, the capillary tube will contain only vapor from the unknown. The burner is removed and the liquid slowly starts to cool. When the vapor pressure falls below atmospheric pressure, liquid will start to enter the capillary tube. This temperature, at which vapor pressure equals atmospheric pressure, is the boiling point.

Figure 14.4 Boiling point determination.

As noted above, ΔH_vap is calculated from the slope of the graph of ln P vs. 1/T, where P is the vapor pressure of the liquid at temperature T in Kelvins. The vapor pressures must be calculated from recorded volumes.

The syringe contains both air and vapor from the liquid sample. As the temperature is increased, two things happen: conditions of pressure and volume change for the air and more of the liquid vaporizes. At each temperature, the liquid is assumed to be in equilibrium with the vapor.

The pressure inside the syringe is equal to the barometric pressure, P_B, and is the sum of the pressure of the sample, P_S, and the pressure of the air, P_A (Dalton’s law):

The pressure of the sample is what we need to know; it is the vapor pressure of the liquid:

An expression for the pressure of air at each temperature is obtained from the combined gas law:

The left side of the equation represents the initial conditions: the volume of air (V_R) in the syringe at room temperature (T_R) and the barometric pressure (P_B). The right side of the equation represents a second set of conditions: pressure and volume at some higher temperature. Solve the equation for pressure of air, P_A:

Equation (4) can now be substituted into equation (2):

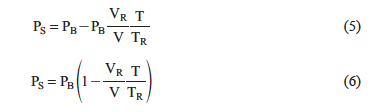
In your analysis, calculate the pressure of the sample at each set of conditions.

Graph ln P_S vs. 1/T for each of the four samples. Include the three known compounds on the same graph. Prepare a second graph for your unknown compound. Include the boiling point for each compound on the graph. The vapor pressure for the boiling points taken from the literature is 760.0 mm Hg. For the experimentally determined boiling point, the vapor pressure is the barometric pressure. Each student must independently generate their graphs.

It is suggested you use a graphing program (e.g., Excel) for your calculations and graphs. If you make your worksheets look like those in the lab manual, you can submit them in place of the Report Sheets in the manual (without having to copy all the data to the Report Sheet). However, you must turn in the Report Sheet (even if blank). If data is copied to the Report Sheet, you still need to turn in the worksheets with your graphs.

In the graphing program, add a linear line to each data set. Set the option to print the equation for the line and the R² values (correlation coefficient). In your report, discuss how the slope is calculated from the equation, and use that slope to calculate ΔH_vap.

For the sample calculation for ΔH_vap you should show a sample calculation for the slope of one of the lines, even if you use the slope generated by the program.

Using the slope of the “best fit” line for each sample, calculate ΔH_vap (kJ · mol²¹).

In your conclusion, report the value of ΔH_vap for your unknown and discuss the trend in ΔH_vap for the three knowns.

Materials Required

Equipment

30-mL syringe
2-mL syringe with needle
two serum stoppers
thermometer
600-mL beaker
100-mL beaker
4-mL test tube
capillary tube
rubber bands
Bunsen burner, wire gauze
thin-walled rubber tubing
ring stand, ring
utility clamp

Common Equipment

none

Chemicals

One of the following compounds:

Set 1—Alcohols

methanol

ethanol

1-propanol

unknown sample
acetone
Set 2—Alkanes

n-hexane

n-heptane

n-octane

Cautions

Be careful to avoid burns from the ring, beaker, and open flame. Vapors from the organic unknowns can be irritating. Fume hoods should be on.

Procedure

Your TA will assign you to a group for Part A—each student does a different known in the assigned set. Your TA will also distribute an unknown.

A. Determine temperature–volume data for the known compound.

Clean and dry a 30-mL syringe. Remove the glass plunger from the syringe and rinse it with a 5-mL portion of acetone. Lubricate the plunger with graphite by rubbing the entire surface with a pencil. Temporarily place the plunger in a 400-mL beaker. Rinse the barrel with acetone using two 5-mL portions. Dry the barrel by drawing air through it with the aspirator.
Attach a serum stopper to the syringe. The small end of the serum stopper goes around the small metal tube of the Luer-Lok fitting. The larger end of the serum stopper is folded back around the outside. See Figure 14.5. The preferred method is to fold the serum stopper back on itself before pushing it onto the Luer-Lok fitting. Do not pull the stopper back too tightly as this will cause leaks—the slits in the metal fitting should not be covered (see Figure 14.5).

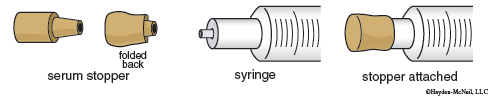
Figure 14.5 Attaching the serum stopper to the syringe.

Insert a loose hypodermic needle into the center of the serum stopper. This allows air to escape as you replace the plunger. Push the plunger down to about the 5-mL mark, and remove the needle. The plunger should turn easily in the barrel but should not spin freely. Test the plunger now.
Use two rubber bands to attach a thermometer to the syringe with the bulb near the 1-mL mark.
Position a ring on the ring stand at a height such that a burner can be placed beneath it. Above the ring, place a utility clamp and use it to hold the syringe, clamping it just below the top of the barrel. Do not clamp too tightly or the movement of the plunger will be restricted. Record the temperature and volume of air in the syringe.
Clean a small syringe and rinse it with a portion of the known compound. Use the small syringe to inject 0.20 mL of the compound into the 30-mL syringe through the serum stopper. Do not inject any more air with the sample. Remove the small syringe.
Position a 600-mL beaker containing room temperature water on the ring. Lower the clamp so that the syringe is immersed at least to the 26-mL mark. Your setup should look like Figure 14.3.
Gently heat the water, stirring with a stirring rod to assure uniform temperature. Heating must be slow enough so that the sample is at the same temperature as the bath and has established its equilibrium. When the volume reaches approximately 8 mL, rotate the plunger and record the temperature and volume. (For 1-propanol and n-octane, take readings at approximately 7 mL.)
Continue heating and stirring; record temperatures and volumes at approximately 12, 16, 20, and 24 mL. (For 1-propanol, take readings at approximately 9, 11, 13, and 15 mL. For n-octane, take readings at approximately 8, 9, 10, and 11 mL.) It is better to remove the flame when readings are being taken.
Measure the barometric pressure using the barometer in the balance room.
The temperature–volume data for your known compound is shared with the two designated students who have known compounds in your set. Obtain their names and temperature– volume data so that you have data for the three compounds in your known set.
Look up boiling points for the three compounds in your known set online. Cite your source in your report.

B. Determine temperature–volume data for the unknown compound.

Repeat steps 1 through 9 with the unknown in place of the known compound. Clean the syringe and use a new serum stopper. Start again with room temperature water in the beaker. Take readings at approximately 8, 12, 16, 20, and 24 mL.

C. Determine the boiling point of the unknown compound.

Rubber band a thermometer to a 4-mL test tube and place 1 mL of your unknown liquid in the test tube. Break off a capillary tube 3 cm from the closed end. Place the capillary, open end down, in the test tube with the sample. The thermometer and test tube with sample are now placed in a water bath contained in a 100-mL beaker (about half full). The water should be at room temperature (see Figure 14.4).
Begin slowly heating the water bath and watch the sample closely. You are looking for bubbles coming from the open end of the capillary. When you have observed a steady stream of bubbles for several seconds, remove the flame.
When liquid starts to enter the capillary tube, record the temperature. This is the boiling point of the liquid.

Waste Disposal

Excess unknown compound and acetone are disposed in the beaker for organic waste, and the waste disposal sheet should be properly filled in. Your lab instructor will dispose of the total volume in the appropriate container.