Chapter 14. Determining ΔG°, ΔH°, and ΔS°

Objectives

Laboratory 22
false
false
  • Understand the relationship between ΔG°, ΔH°, ΔS°, and Ksp and how they may be determined experimentally.
  • Explore the relationship between ΔG° and Ksp and the temperature effect on the two.

Adapted from Butler, W.B., Kirschenbaum, L. K., & Ruckberg, B. J. Chem. Ed. 2000. 77, 1039–1040

Introduction

Thermodynamics is the study of energy and how it is converted from one form to another. Thermodynamic principles are included in a variety of scientific disciplines including physics, chemistry, biology, engineering, and material science. Thermodynamics plays an important role in any situation involving heat or energy. Recently, a considerable amount of attention, from scientists and politicians alike, has focused on generating cleaner, renewable energy, and fuels.

Discussion

22.1 Connection to Lecture

In earlier chemistry courses we learned about enthalpy, a state function allowing us to account for the heat flow in processes occurring at constant pressure. In lecture we are studying chemical reactions and determining if they occur spontaneously. We are finding that the spontaneity is determined by, not only the enthalpy, but also the entropy and often the temperature. The Gibbs free energy term, ΔG, has been introduced and relates the enthalpy, entropy, and temperature to determine the spontaneity.

ΔG° = ΔH° − TΔS°

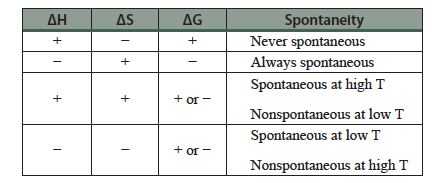
For spontaneous reactions, ΔG° is a negative value. Likewise, a positive ΔG° is indicative of a nonspontaneous reaction. We may predict the signs of ΔH° and ΔS°.

Question 22.1: Using your previous general chemistry knowledge, give some general guidelines for predicting the sign of ΔH° in terms of breaking and forming bonds.

A higher entropy corresponds to a greater dispersal of energy and a positive ΔS°. Some examples include changing from a solid to a liquid, from a liquid to a gas, or from fewer moles of reactants to greater moles of products. The reverse, going to a state of more order, would lead to a negative ΔS°. Using the equation above and the signs of ΔH° and ΔS° we may predict the sign of ΔG° and hence the spontaneity.

Table 22.1 Relating the signs of ΔH and ΔS to the sign of ΔG using ΔG = ΔH – TΔS.

In certain situations we can call a reaction always spontaneous or never spontaneous. However, there are cases in which the spontaneity will depend on temperature. The melting and forming of ice is a classic example. If you put water in the freezer, the water will spontaneously form ice. Likewise, if you put an ice cube on the table at room temperature, the ice will spontaneously melt.

Question 22.2: Which scenario from Table 22.1 above is consistent with what we know about the melting and forming of ice as a function of temperature?

22.2 Titration of a Saturated Solution

In this experiment we will determine ΔG° for Ca(OH)2 using an experimentally determined solubility product constant. We will use the same approach used in the last lab to find this Ksp. The equation and expression for the slightly soluble calcium hydroxide is:

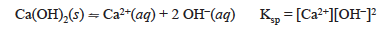
As in the previous lab, in order to determine this Ksp you will need to titrate the saturated solution. For this system we will be doing an acid–base titration to find the hydroxide concentration. A standardized HCl solution will be provided to you. The indicator will be bromothymol blue. This indicator will turn the initial solution blue. As the titration progresses the solution will turn green and at the end point the solution will turn yellow, indicating the equivalence point has been reached.

Question 22.3: What will be the mole ratio of H+ to OH− once the equivalence point is reached?

This will be completed at two different temperatures. As with the previous lab, you will be titrating a saturated solution. In order to measure the concentration of ions in solution at saturation, it will be important to filter your solution to remove the solid just prior to titrating.

22.3 Data Analysis

Once the Ksp is found, we may relate it to Gibbs free energy.

ΔG° = −RT ln Ksp

We know that the Ksp, and hence the ΔG, will change with changing temperature. In this lab you will find a Ksp at two different temperatures and the corresponding ΔG’s.

On the other hand, ΔH and ΔS effectively remain constant with varying temperature. Knowing the ΔG values for two different temperatures we have a system of two equations with two unknowns. Using algebra we may calculate both ΔH and ΔS for the calcium hydroxide system.

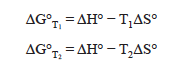
Question 22.4: Would you expect a positive or negative ΔH for the dissolution of Ca(OH)2? Would you expect a positive or negative ΔS for the dissolution of Ca(OH)2?

Materials Required

Equipment

  • two 125-mL Erlenmeyer flasks
  • 250-mL beaker
  • 100-mL graduated cylinder
  • 10.00-mL pipet, bulb
  • 25-mL buret, clamp
  • plastic funnel, filter paper
  • Bunsen burner, ring, wire gauze
  • −20 °C to 100 °C thermometer

Chemicals

  • standardized 0.01xx M hydrochloric acid, HCl
  • bromothymol blue solution
  • saturated Ca(OH)2, calcium hydroxide solution (room temp)
  • solid Ca(OH)2, calcium hydroxide

Common Equipment

  • top-loading balance

Cautions

Avoid burns from the ring, wire gauze, beaker, and open flame. Goggles must be worn at all times.

Procedure

All buret readings should be recorded to the nearest 0.01 mL. Answer questions in your lab notebook as you go along. Discussions with your peers and TA are encouraged.

A. Solubility of calcium hydroxide at room temperature.
  1. A solution of calcium hydroxide will be stirring at room temperature in the balance room. Using a beaker obtain approximately 40 mL of this saturated solution and record the temperature.
  2. To ensure no solid is present, use a clean, dry long-stem funnel and filter paper with medium porosity to filter the sample.
  3. Pipet 10.00 mL of the filtered saturated solution into a clean 125-mL Erlenmeyer flask. To this flask also add 25 mL of distilled water and a few drops of the bromothymol blue indicator.

Question 22.5: When adding the 25 mL of distilled water, you are changing the ion concentration. Why does this not matter?

  1. Using a buret and proper titration techniques, titrate this sample using the standardized HCl solution until the yellow end point is reached.
  2. Repeat steps 3 and 4 to perform two additional titrations.
B. Solubility of calcium hydroxide at high temperature.
  1. Bring 100 mL of distilled water to a boil in a 250-mL beaker.
  2. After the water has been boiling for several minutes, add about 2 grams of Ca(OH)2 to the water while stirring. Continue to boil gently for about 5 minutes with occasional stirring and then turn off your burner. Clean and dry a long-stem funnel for the next step while waiting.
  3. Quickly filter 40–50 mL of the hot solution using the clean long-stem funnel and medium porosity filter paper. Measure the temperature of this solution just before filtering. Note: You are asked to filter quickly because the concentration of the ions can change as the solution cools.
  4. After the solid Ca(OH)2 has been removed allow the solution to cool. Pipet 10.00 mL of this filtered solution into a clean, dry 125-mL Erlenmeyer flask. Add about 25 mL of distilled water and a few drops of the bromothymol blue indicator.
  5. Titrate the sample with the standardized HCl solution until the yellow end point is reached.
  6. Repeat this titration (steps 9 and 10) two additional times for a total of three titrations.
  7. Calculate the moles of hydroxide ions for all six of your titrations.
  8. Continue on with your calculations for the molarity of hydroxide, Ksp, and ΔG° at both temperatures.
  9. Using the ΔG° values obtained at both temperatures, calculate the ΔH° and ΔS°.

Waste Disposal

All solutions may be rinsed down the drain.

Points to Consider

In this lab you are calculating a Ksp from titration data obtained in the lab at two temperatures. You are also calculating ΔG° at two temperatures and determining ΔH° and ΔS°.

  • Comment on how your calculated Ksp values compare to that in the CRC. How does this relate to the concentration you determined from titration?
  • Write the equilibrium expression to rationalize your explanation.
  • How do the values for ΔG° at two temperatures compare to each other?
  • What were the ΔH° and ΔS° values you determined? Do the signs of these make sense based on the material you are learning in lecture? Does the sign of ΔH° shift to favor the reactants or products? From lecture content, would you predict the sign of ΔS° to be positive or negative?
  • What can you say about the solubility properties of calcium hydroxide as a function of temperature? Is this what you expected?