Let’s say that the mean number of physical symptoms (like pain) experienced by the participants in each of the three groups was about the same at the beginning of the health-promotion study. A year later, the number of symptoms had decreased in the two intervention groups but had remained stable in the control group. This may or may not be a meaningful result. We would expect the average number of symptoms to be somewhat different for each of the three groups because each group consisted of different people. And we would expect some fluctuation in level over time, due simply to chance. But are the differences in the number of symptoms between the intervention groups and the control group large enough not to be due to chance alone? If other researchers conducted the same study with different participants, would they be likely to get the same general pattern of results? To answer such questions, we turn to inferential statistics. Inferential statistics guide us in determining what inferences, or conclusions, can legitimately be drawn from a set of research findings.

Depending on the data, different inferential statistics can be used to answer questions such as the ones raised in the preceding paragraph. For example, t tests are used to compare the means of two groups. Researchers could use a t test, for instance, to compare average energy level at the end of the study in the traditional and alternative groups. Another t test could compare the average energy level at the beginning and end of the study within the alternative group. If we wanted to compare the means of more than two groups, another technique, analysis of variance (often abbreviated as ANOVA), could be used. Each inferential statistic helps us determine how likely a particular finding is to have occurred as a matter of nothing more than chance or random variation. If the inferential statistic indicates that the odds of a particular finding occurring are considerably greater than mere chance, we can conclude that our results are statistically significant. In other words, we can conclude with a high degree of confidence that the manipulation of the independent variable, rather than simply chance, is the reason for the results.

To see how this works, let’s go back to the normal curve for a moment. Remember that we know exactly what percentage of a normal curve falls between any two z scores. If we choose one person at random out of a normal distribution, what is the chance that this person’s z score is above +2? If you look at FIGURE A.9 (it’s the same as FIGURE A.5), you will see that about 2.1 percent of the curve lies above a z score (or standard deviation unit) of +2. Therefore, the chance, or probability, that the person we choose will have a z score above +2 is .0228 (or 2.28 chances out of 100). That’s a pretty small chance. If you study the normal curve, you will see that the majority of cases (about 96 percent) fall between -2 and +2 SDs, so in choosing a person at random, that person is not likely to fall above a z score of +2.

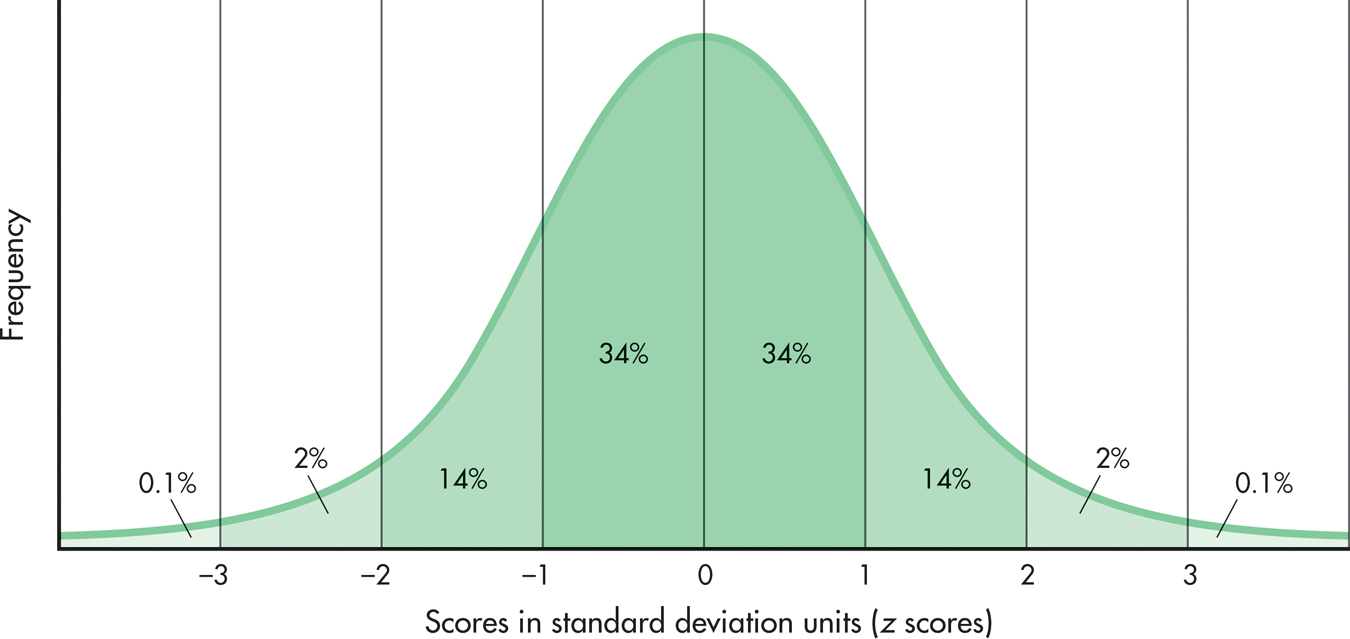
When researchers test for statistical significance, they usually employ statistics other than z scores, and they may use distributions that differ in shape from the normal curve. The logic, however, is the same. They compute some kind of inferential statistic that they compare to the appropriate distribution. This comparison tells them the likelihood of obtaining their results if chance alone is operating.

The problem is that no test exists that will tell us for sure whether our intervention or manipulation “worked”; we always have to deal with probabilities, not certainties. Researchers have developed some conventions to guide them in their decisions about whether or not their study results are statistically significant. Generally, when the probability of obtaining a particular result if random factors alone are operating is less than .05 (5 chances out of 100), the results are considered statistically significant. Researchers who want to be even more sure set their probability value at .01 (1 chance out of 100).

Because researchers deal with probabilities, there is a small but real possibility of erroneously concluding that study results are significant; this is called a Type I error. The results of one study, therefore, should never be completely trusted. For researchers to have greater confidence in a particular effect or result, the study should be repeated, or replicated. If the same results are obtained in different studies, then we can be more certain that our conclusions about a particular intervention or effect are correct.

There is a second decision error that can be made—a Type II error. This is when a researcher fails to find a significant effect, yet that significant effect really exists. A Type II error results when a study does not have enough power; in a sense, the study is not strong enough to find the effect the researcher is looking for. Higher power may be achieved by improving the research design and measuring instruments, or by increasing the number of participants or subjects being studied.

One final point about inferential statistics. Are the researchers interested only in the changes that might have occurred in the small groups of people participating in the health-promotion study, or do they really want to know whether the interventions would be effective for people in general? This question focuses on the difference between a population and a sample. A population is a complete set of something—people, nonhuman animals, objects, or events. The researchers who designed this study wanted to know whether the interventions they developed would benefit all people (or, more precisely, all people between the ages of 20 and 56). Obviously, they could not conduct a study on this entire population. The best they could do was choose some portion of that population to serve as subjects; in other words, they selected a sample. The study was conducted on this sample. The researchers analyzed the sample results, using inferential statistics to make guesses about what they would have found had they studied the entire population. Inferential statistics allow researchers to take the findings they obtain from a sample and apply them to a population.

So what did the health-promotion study find? Did the interventions work? The answer is “yes,” sort of. The traditional and alternative treatment groups, when combined, improved more than did the no-treatment control group. At the end of the study, participants in the two intervention programs had better self-perceptions regarding health, better mood, more energy, and fewer physical symptoms. Compared with the traditional and the no-treatment groups, the alternative group showed greater improvement in health perceptions and a significant decrease in depression and the use of prescription drugs. Interestingly, participation in the treatment groups did not generally result in changes in health risk, such as lowered blood pressure or decreased weight. The researchers believe that little change occurred because the people who volunteered for the study were basically healthy individuals. The study needs to be replicated with a less healthy sample. In sum, the intervention programs had a greater effect on health perceptions and psychological variables than on physical variables. The researchers concluded that a health-promotion regimen (either traditional or alternative) is helpful. I’m sure other studies will be conducted to explore these issues further!