The genetic approach that reveals the interacting genes for a particular biological property is briefly as follows:

Gene interaction is inferred from the phenotype of the double mutant: if the genes interact, then the phenotype differs from the simple combination of both single-gene mutant phenotypes. If mutant alleles from different genes interact, then we infer that the wild-type genes interact normally as well. In cases in which the two mutants interact, a modified 9:3:3:1 Mendelian ratio will often result.

A procedure that must be carried out before testing interactions is to determine whether each mutation is of a different locus (step 2 above). The mutant screen could have unintentionally favored certain genes. Thus, the set of gene loci needs to be defined, as shown in the next section.

How is it possible to decide whether two mutations belong to the same gene? There are several ways. First, each mutant allele could be mapped. Then, if two mutations map to two different chromosomal loci, they are likely of different genes. However, this approach is time consuming on a large set of mutations. A quicker approach often used is the complementation test.

In a diploid, the complementation test is performed by intercrossing two individuals that are homozygous for different recessive mutations. The next step is to observe whether the progeny have the wild-type phenotype. If the progeny are wild type, the two recessive mutations must be in different genes because the respective wild-type alleles provide wild-type function. In this case, the two mutations are said to have complemented. Here, we will name the genes a1 and a2, after their mutant alleles. We can represent the heterozygotes as follows, depending on whether the genes are on the same chromosome or are on different chromosomes:

Different chromosomes:

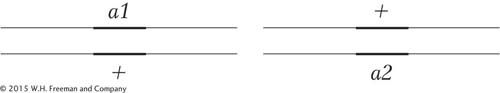
Same chromosome (shown in the trans configuration):

However, if the progeny are not wild type, then the recessive mutations must be alleles of the same gene. Because both alleles of the gene are mutants, there is no wild-type allele to help distinguish between two different mutant alleles of a gene whose wild-type allele is a⁺. These alleles could have different mutant sites within the same gene, but they would both be nonfunctional. The heterozygote ai a’ would be

228

At the operational level, complementation is defined as the production of a wild-type phenotype when two haploid genomes bearing different recessive mutations are united in the same cell.

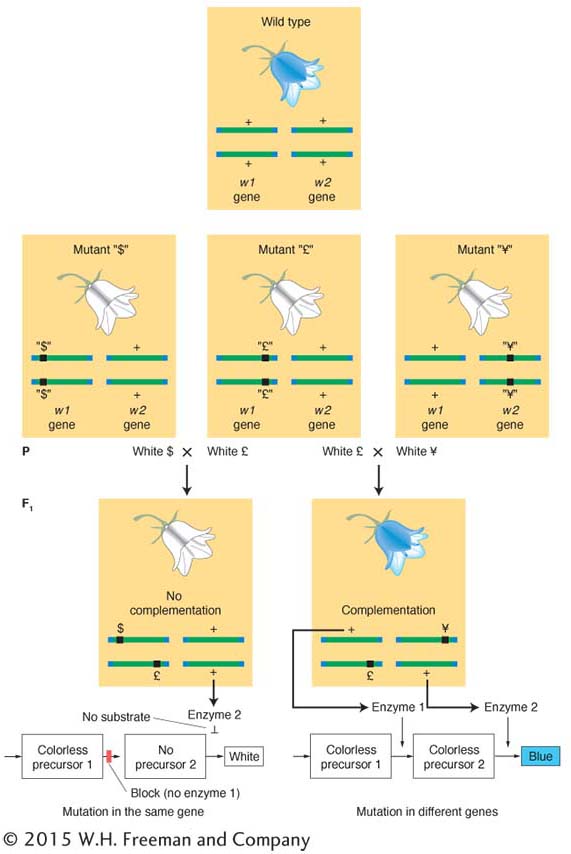
Let’s illustrate the complementation test with an example from harebell plants (genus Campanula). The wild-type flower color of this plant is blue. Let’s assume that, from a mutant hunt, we have obtained three white-petaled mutants and that they are available as homozygous pure-breeding strains. They all look the same, and so we do not know a priori whether they are genetically identical. We will call the mutant strains $, £, and ¥ to avoid any symbolism using letters, which might imply dominance. When crossed with wild type, each mutant gives the same results in the F₁ and F₂ as follows:

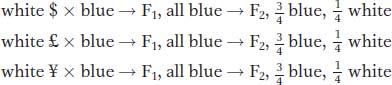
In each case, the results show that the mutant condition is determined by the recessive allele of a single gene. However, are they three alleles of one gene, of two genes, or of three genes? Because the mutants are recessive, the question can be answered by the complementation test, which asks if the mutants complement one another.

Let us intercross the mutants to test for complementation. Assume that the results of intercrossing mutants $, £, and ¥ are as follows:

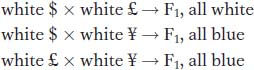
From this set of results, we can conclude that mutants $ and £ must be caused by alleles of one gene (say, w1) because they do not complement, but ¥ must be caused by a mutant allele of another gene (w2) because ¥ complements both $ and £.

How does complementation work at the molecular level? The normal blue color of the harebell flower is caused by a blue pigment called anthocyanin. Pigments are chemicals that absorb certain colors of light; in regard to the harebell, the anthocyanin absorbs all wavelengths except blue, which is reflected into the eye of the observer. However, this anthocyanin is made from chemical precursors that are not pigments; that is, they do not absorb light of any specific wavelength and simply reflect back the white light of the sun to the observer, giving a white appearance. The blue pigment is the end product of a series of biochemical conversions of nonpigments. Each step is catalyzed by a specific enzyme encoded by a specific gene. We can explain the results with a pathway as follows:

229

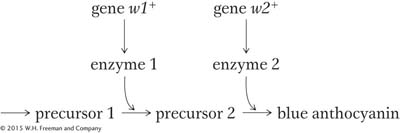
A homozygous mutation in either of the genes will lead to the accumulation of a precursor that will simply make the plant white. Now the mutant designations could be written as follows:

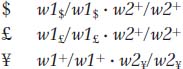
However, in practice, the subscript symbols would be dropped and the genotypes would be written as follows:

Hence, an F₁ from $ × £ will be

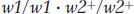
These F₁ plants will have two defective alleles for w1 and will therefore be blocked at step 1. Even though enzyme 2 is fully functional, it has no substrate on which to act; so no blue pigment will be produced and the phenotype will be white.

The F₁ plants from the other crosses, however, will have the wild-type alleles for both of the enzymes needed to take the intermediates to the final blue product. Their genotypes will be

Hence, we see that complementation is actually a result of the cooperative interaction of the wild-type alleles of the two genes. Figure 6-12 summarizes the interaction of the complementing and noncomplementing white mutants at the genetic and cellular levels.

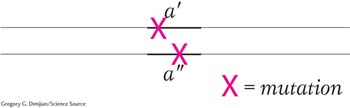
In a haploid organism, the complementation test cannot be performed by intercrossing. In fungi, an alternative method brings mutant alleles together to test complementation: fusion resulting in a heterokaryon (Figure 6-13). Fungal cells fuse readily. When two different strains fuse, the haploid nuclei from the different strains occupy one cell, which is the heterokaryon (Greek; different kernels). The nuclei in a heterokaryon do not generally fuse. In one sense, this condition is a “mimic” diploid.

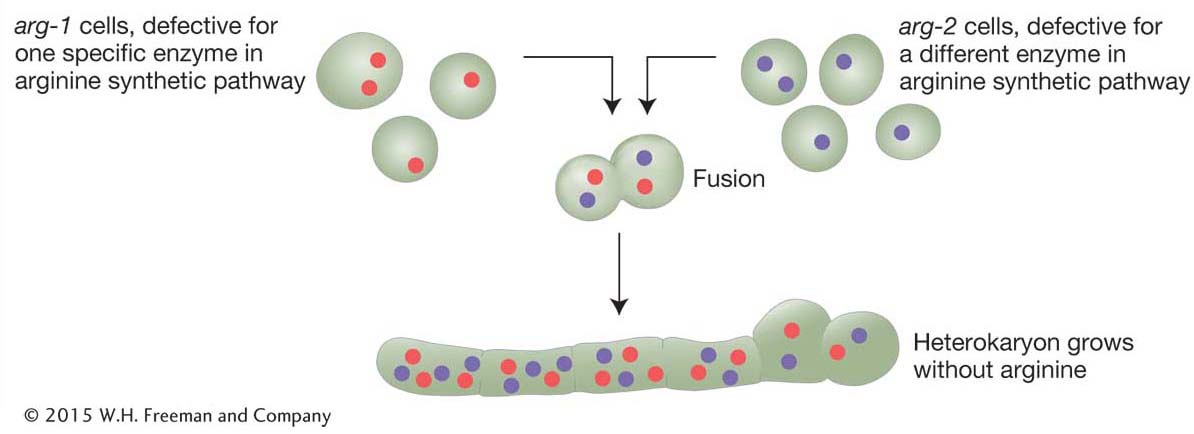
Assume that, in different strains, there are mutations in two different genes conferring the same mutant phenotype—for example, an arginine requirement. We will call these genes arg-1 and arg-2. The genotypes of the two strains can be represented as arg-1 · arg-2⁺ and arg-1⁺ · arg-2. These two strains can be fused to form a heterokaryon with the two nuclei in a shared cytoplasm:

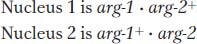
230

Because gene products are made in a common cytoplasm, the two wild-type alleles can exert their dominant effect and cooperate to produce a heterokaryon of wild-type phenotype. In other words, the two mutations complement, just as they would in a diploid. If the mutations had been alleles of the same gene, there would have been no complementation.

231

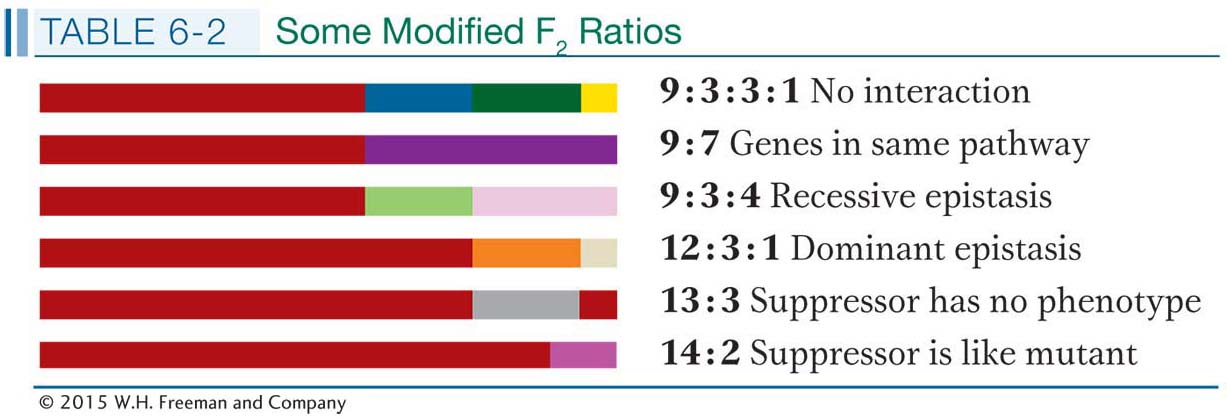
Recall that, to learn whether two genes interact, we need to assess the phenotype of the double mutant to see if it is different from the combination of both single mutations. The double mutant is obtained by intercrossing. The F₁ is obtained as part of the complementation test; so with the assumption that complementation has been observed, suggesting different genes, the F₁ is selfed or intercrossed to obtain an F₂ homozygous for both mutations. This double mutant may then be identified by looking for Mendelian ratios. For example, if a standard 9:3:3:1 Mendelian ratio is obtained, the phenotype present in only 1/16 of the progeny represents the double mutant (the “1” in 9:3:3:1). In cases of gene interaction, however, the phenotype of the double mutant may not be distinct but will match that of one of the single mutants. In this case, a modified Mendelian ratio will result, such as 9:3:4 or 9:7.

The standard 9:3:3:1 Mendelian ratio is the simplest case, expected if there is no gene interaction and if the two mutations under test are on different chromosomes. This 9:3:3:1 ratio is the null hypothesis: any modified Mendelian ratio representing a departure from this null hypothesis would be informative, as the following examples will show.

The 9:3:3:1 ratio: no gene interaction As a baseline, let’s start with the case in which two mutated genes do not interact, a situation where we expect the 9:3:3:1 ratio. Let’s look at the inheritance of skin coloration in corn snakes. The snake’s natural color is a repeating black-and-orange camouflage pattern, as shown in Figure 6-14a. The phenotype is produced by two separate pigments, both of which are under genetic control. One gene determines the orange pigment, and the alleles that we will consider are o⁺ (presence of orange pigment) and o (absence of orange pigment). Another gene determines the black pigment, and its alleles are b⁺ (presence of black pigment) and b (absence of black pigment). These two genes are unlinked. The natural pattern is produced by the genotype o⁺/−; b⁺/−. (The dash represents the presence of either allele.) A snake that is o/o; b⁺/− is black because it lacks the orange pigment (Figure 6-14b), and a snake that is o⁺/−; b/b is orange because it lacks the black pigment (Figure 6-14c). The double homozygous recessive o/o; b/b is albino (Figure 6-14d). Notice, however, that the faint pink color of the albino is from yet another pigment, the hemoglobin of the blood that is visible through this snake’s skin when the other pigments are absent. The albino snake also clearly shows that there is another element to the skin-pigmentation pattern in addition to pigment: the repeating motif in and around which pigment is deposited.

232

If a homozygous orange and a homozygous black snake are crossed, the F₁ is wild type (camouflaged), demonstrating complementation:

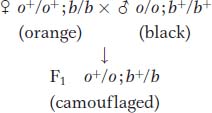
Here, however, an F₂ shows a standard 9:3:3:1 ratio:

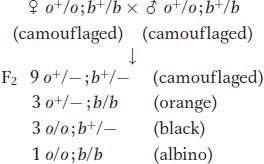
The 9:3:3:1 ratio is produced because the two pigment genes act independently at the cellular level.

If the presence of one mutant makes one pathway fail, the other pathway is still active, producing the other pigment color. Only when both mutants are present do both pathways fail, and no pigment of any color is produced.

The 9 : 7 ratio: genes in the same pathway The F₂ ratio from the harebell dihybrid cross shows both blue and white plants in a ratio of 9:7. How can such results be explained? The 9:7 ratio is clearly a modification of the dihybrid 9:3:3:1 ratio with the 3:3:1 combined to make 7; hence, some kind of interaction is inferred. The cross of the two white lines and subsequent generations can be represented as follows:

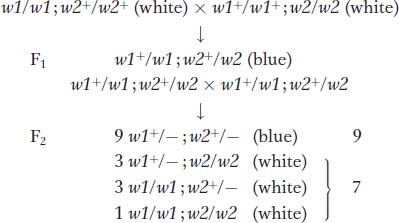
233

Clearly, in this case, the only way in which a 9:7 ratio is possible is if the double mutant has the same phenotypes as the two single mutants. Hence, the modified ratio constitutes a way of identifying the double mutant’s phenotype. Furthermore, the identical phenotypes of the single and double mutants suggest that each mutant allele controls a different step in the same pathway. The results show that a plant will have white petals if it is homozygous for the recessive mutant allele of either gene or both genes. To have the blue phenotype, a plant must have at least one copy of the dominant allele of both genes because both are needed to complete the sequential steps in the pathway. No matter which is absent, the same pathway fails, producing the same phenotype. Thus, three of the genotypic classes will produce the same phenotype, and so, overall, only two phenotypesre suit.

The example in harebells entailed different steps in a synthetic pathway. Similar results can come from gene regulation. A regulatory gene often functions by producing a protein that binds to a regulatory site upstream of a target gene, facilitating the transcription of the gene (Figure 6-15). In the absence of the regulatory protein, the target gene would be transcribed at very low levels, inadequate for cellular needs. Let’s cross a pure line r/r defective for the regulatory protein to a pure line a/a defective for the target protein. The cross is r/r; a⁺/a⁺ × r⁺/r⁺; a/a. The r⁺/r; a⁺/a dihybrid will show complementation between the mutant genotypes because both r⁺ and a⁺ are present, permitting normal transcription of the wild-type allele. When selfed, the F₁ dihybrid will also result in a 9:7 phenotypic ratio in the F₂:

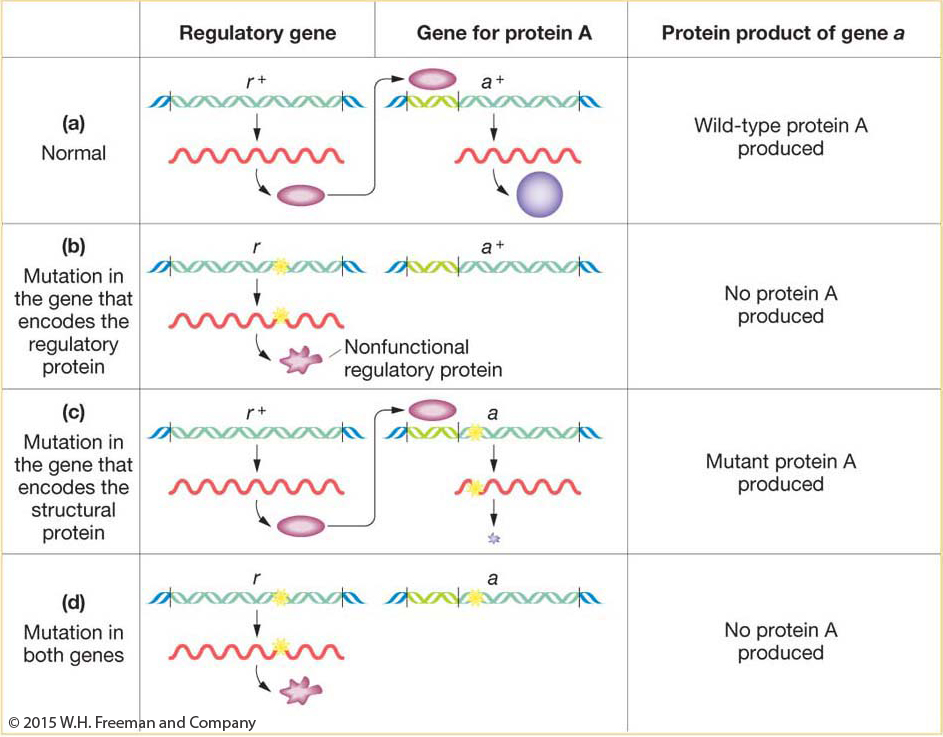
234

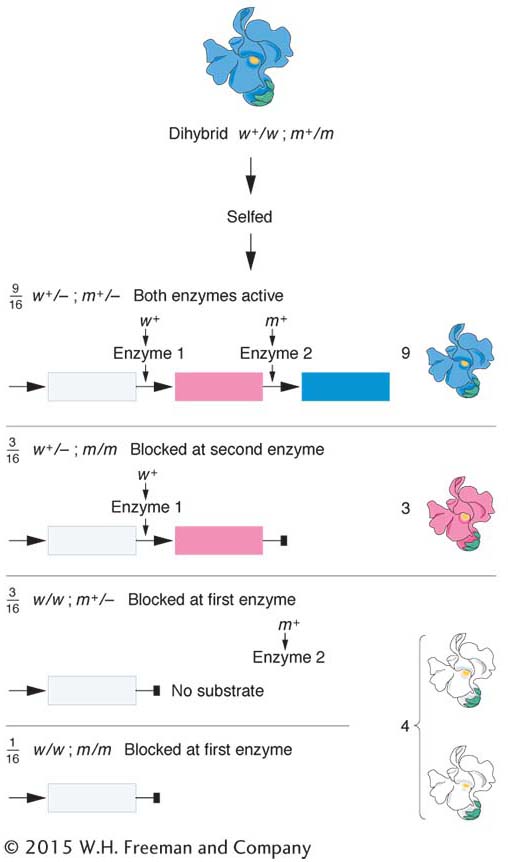
The 9:3:4 ratio: recessive epistasis A 9:3:4 ratio in t he F₂ suggests a type of gene interaction called epistasis. This word means “stand upon,” referring to the situation in which a double mutant shows the phenotype of one mutation but not the other. The overriding mutation is epistatic, whereas the overridden one is hypostatic. Epistasis also results from genes being in the same pathway. In a simple synthetic pathway, the epistatic mutation is carried by a gene that is farther upstream (earlier in the pathway) than the gene of the overridden mutation (Figure 6-16). The mutant phenotype of the upstream gene takes precedence, no matter what is taking place later in the pathway.

Let’s look at an example concerning petal-pigment synthesis in the plant blue-eyed Mary (Collinsia parviflora). From the blue wild type, we’ll start with two pure mutant lines, one with white (w/w) and the other with magenta petals (m/m). The w and m genes are not linked. The F₁ and F₂ are as follows:

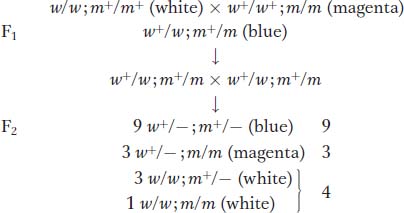
In the F₂, the 9:3:4 phenotypic ratio is diagnostic of recessive epistasis. As in the preceding case, we see, again, that the ratio tells us what the phenotype of the double must be, because the 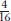component of the ratio must be a grouping of one single mutant class 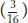plus the double mutant class 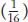. Hence, the double mutant expresses only one of the two mutant phenotypes; so, by definition, white must be epistatic to magenta. (To find the double mutant within the group, white F₂ plants would have to be individually testcrossed.) This interaction is called recessive epistasis because a recessive phenotype (white) overrides the other phenotype. Dominant epistasis will be considered in the next section.

235

At the cellular level, we can account for the recessive epistasis in Collinsia by the following type of pathway (see also Figure 6-16).

Notice that the epistatic mutation occurs in a step in the pathway leading to blue pigment; this step is upstream of the step that is blocked by the masked mutation.

Another informative case of recessive epistasis is the yellow coat color of some Labrador retriever dogs. Two alleles, B and b, stand for black and brown coats, respectively. The two alleles produce black and brown melanin. The allele e of another gene is epistatic on these alleles, giving a yellow coat (Figure 6-17). Therefore, the genotypes B/−; e/e and b/b; e/e both produce a yellow phenotype, whereas B/−; E/− and b/b; E/− are black and brown, respectively. This case of epistasis is not caused by an upstream block in a pathway leading to dark pigment. Yellow dogs can make black or brown pigment, as can be seen in their noses and lips. The action of the allele e is to prevent the deposition of the pigment in hairs. In this case, the epistatic gene is developmentally downstream; it represents a kind of developmental target that must be of E genotype before pigment can be deposited.

In fungi, tetrad analysis is useful in identifying a double mutant. For example, an ascus containing half its products as wild type must contain double mutants. Consider the cross

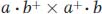
In some proportion of progeny, the alleles a and b will segregate together (a nonparental ditype ascus). Such a tetrad will show the following phenotypes:

236

Hence, the double mutant must be the non-wild-type genotype and can be assessed accordingly. If the phenotype is the a phenotype, then b is being overridden; if the phenotype is the b phenotype, then a is being overridden. If both phenotypes are present, then there is no epistasis.

The 12:3:1 ratio: dominant epistasis In foxgloves (Digitalis purpurea), two genes interact in the pathway that determines petal coloration. The two genes are unlinked. One gene affects the intensity of the red pigment in the petal; allele d results in the light red color seen in natural populations of foxgloves, whereas D is a mutant allele that produces dark red color (Figure 6-18). The other gene determines in which cells the pigment is synthesized: allele w allows synthesis of the pigment throughout the petals as in the wild type, but the mutant allele W confines pigment synthesis to the small throat spots. If we self a dihybrid D/d; W/w, then the F₂ ratio is as follows:

The ratio tells us that the dominant allele W is epistatic, producing the 12:3:1 ratio. The 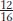component of the ratio must include the double mutant class 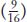, which is clearly white in phenotype, establishing the epistasis of the dominant allele W. The two genes act in a common developmental pathway: W prevents the synthesis of red pigment but only in a special class of cells constituting the main area of the petal; synthesis is allowed in the throat spots. When synthesis is allowed, the pigment can be produced in either high or low concentrations.

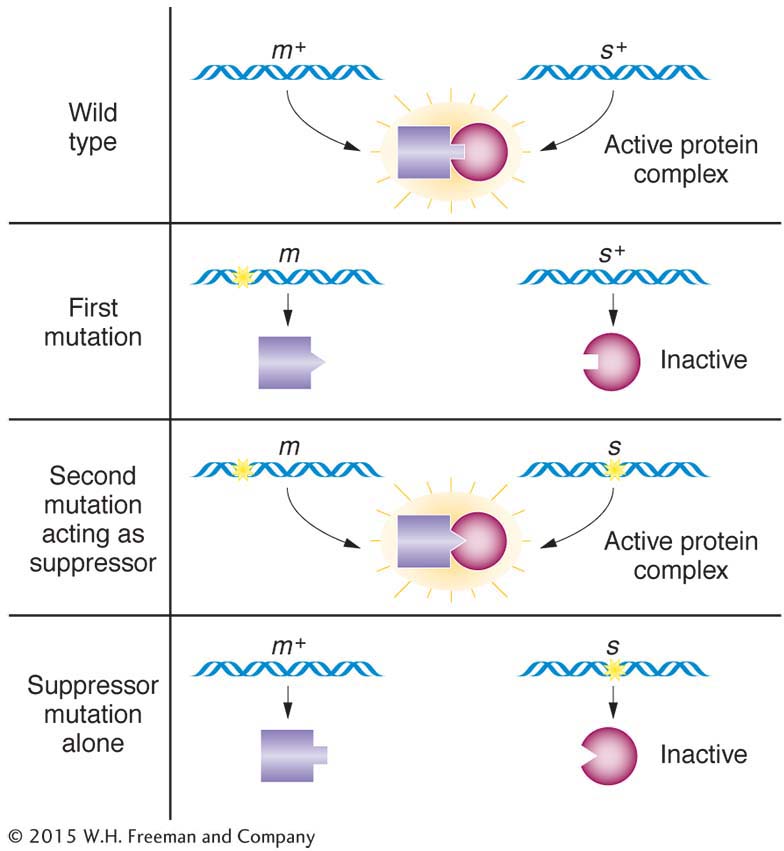
Suppressors It is not easy to specifically select or screen for epistatic interactions, and cases of epistasis have to be built up by the laborious combination of candidate mutations two at a time. However, for our next type of gene interaction, the experimenter can readily select interesting mutant alleles. A suppressor is a mutant allele of a gene that reverses the effect of a mutation of another gene, resulting in a wild-type or near-wild-type phenotype. Suppression implies that the target gene and the suppressor gene normally interact at some functional level in their wild-type states. For example, assume that an allele a⁺ produces the normal phenotype, whereas a recessive mutant allele a results in abnormality. A recessive mutant allele s at another gene suppresses the effect of a, and so the genotype a/a · s/s will have the wild-type (a⁺-like) phenotype. Suppressor alleles sometimes have no effect in the absence of the other mutation; in such a case, the phenotype of a⁺/a^{+ ·} s/s would be wild type. In other cases, the suppressor allele produces its own abnormal phenotype.

Screening for suppressors is quite straightforward. Start with a mutant in some process of interest, expose this mutant to mutation-causing agents such as high-energy radiation, and screen the descendants for wild types. In haploids such as fungi, screening is accomplished by simply plating mutagenized cells and looking for colonies with wild-type phenotypes. Most wild types arising in this way are merely reversals of the original mutational event and are called revertants. However, some will be “pseudorevertants,” double mutants in which one of the mutations is a suppressor.

237

Revertant and suppressed states can be distinguished by appropriate crossing. For example, in yeast, the two results would be distinguished as follows:

The appearance of the original mutant phenotype identifies the parent as a suppressed mutant.

In diploids, suppressors produce various modified F₂ ratios, which are useful in confirming suppression. Let’s look at a real-life example from Drosophila. The recessive allele pd results in purple eye color when unsuppressed. A recessive allele su has no detectable phenotype itself but suppresses the unlinked recessive allele pd. Hence, pd/pd; su/su is wild type in appearance and has red eyes. The following analysis illustrates the inheritance pattern. A homozygous purple-eyed fly is crossed with a homozygous red-eyed stock carrying the suppressor.

The overall ratio in the F₂ is 13 red : 3 purple. The 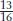component must include the double mutant, which is clearly wild type in phenotype. This ratio is expected from a recessive suppressor that itself has no detectable phenotype.

Suppression is sometimes confused with epistasis. However, the key difference is that a suppressor cancels the expression of a mutant allele and restores the corresponding wild-type phenotype. Furthermore, often only two phenotypes segregate (as in the preceding examples) rather than three, as in epistasis.

How do suppressors work at the molecular level? There are many possible mechanisms. A particularly useful type of suppression is based on the physical binding of gene products in the cell—for example, protein-protein binding. Assume that two proteins normally fit together to provide some type of cellular function. When a mutation causes a shape change in one protein, it no longer fits together with the other; hence, the function is lost (Figure 6-19). However, a suppressor mutation that causes a compensatory shape change in the second protein can restore fit and hence normal function. In this figure, if the genotypes were diploids representing an F₂ from a dihybrid, then a 14:2 ratio would result because the only mutant genotypes would be m/m · s⁺/s⁺ (1i16) and m⁺/m⁺ · s/s (1/16), totaling 2/16. If this were a haploid dihybrid cross (such as m⁺ s⁺ × m s), a 1:1 ratio would result. From suppressor ratios generally, interacting proteins often can be deduced.

238

Alternatively, in situations in which a mutation causes a block in a metabolic pathway, the suppressor finds some way of bypassing the block—for example, by rerouting into the blocked pathway intermediates similar to those beyond the block. In the following example, the suppressor provides an intermediate B to circumvent the block.

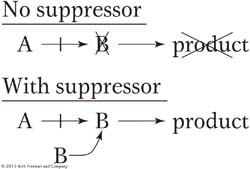
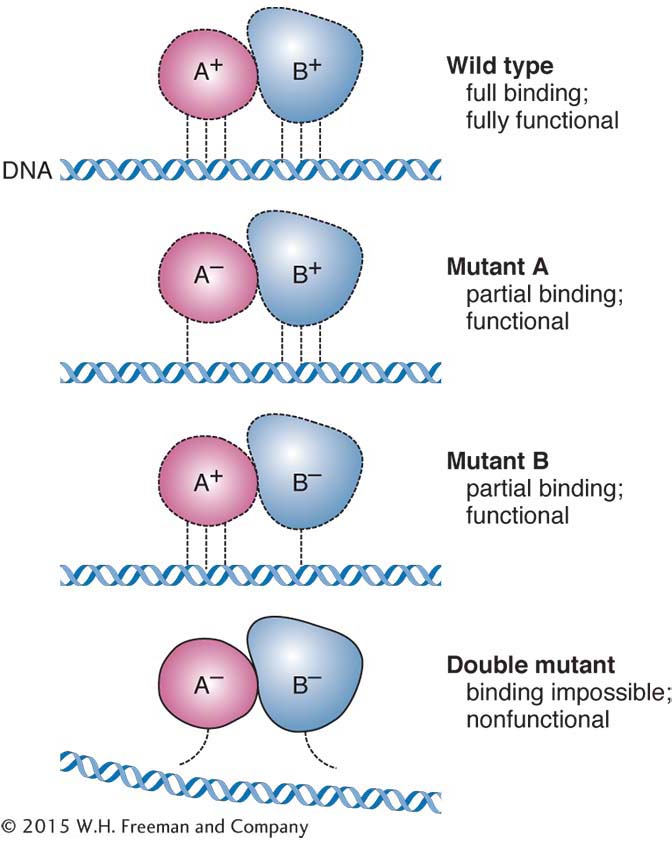
In several organisms, nonsense suppressors have been found—mutations in tRNA genes resulting in an anticodon that will bind to a premature stop codon within a mutant coding sequence. Hence, the suppressor allows translation to proceed past the former block and make a complete protein rather than a truncated one. Such suppressor mutations often have little effect on the phenotype other than in suppression.

Modifiers As the name suggests, a modifier mutation at a second locus changes the degree of expression of a mutated gene at the first locus. Regulatory genes provide a simple illustration. As in an earlier example, regulatory proteins bind to the sequence of the DNA upstream of the start site for transcription. These proteins regulate the level of transcription. In the discussion of complementation, we considered a null mutation of a regulatory gene that almost completely prevented transcription. However, some regulatory mutations change the level of transcription of the target gene so that either more or less protein is produced. In other words, a mutation in a regulatory protein can down-regulate or up-regulate the transcribed gene. Let’s look at an example using a down-regulating regulatory mutation b, affecting a gene A in a fungus such as yeast. We look at the effect of b on a leaky mutation of gene A. A leaky mutation is one with some low level of gene function. We cross a leaky mutation a with the regulatory mutation b:

leaky mutant a · b⁺ × inefficient regulator a⁺ · b

Hence, the action of the modifier is seen in the appearance of two grades of mutant phenotypes within the a progeny.

239

Synthetic lethals In some cases, when two viable single mutants are intercrossed, the resulting double mutants are lethal. In a diploid F₂, this result would be manifested as a 9:3:3 ratio because the double mutant (which would be the “1” component of the ratio) would be absent. These synthetic lethals can be considered a special category of gene interaction. They can point to specific types of interactions of gene products. For instance, genome analysis has revealed that evolution has produced many duplicate systems within the cell. One advantage of these duplicates might be to provide “backups.” If there are null mutations in genes in both duplicate systems, then a faulty system will have no backup, and the individual will lack essential function and die. In another instance, a leaky mutation in one step of a pathway may cause the pathway to slow down, but leave enough function for life. However, if double mutants combine, each with a leaky mutation in a different step, the whole pathway grinds to a halt. One version of the latter interaction is two mutations in a protein machine, as shown in Figure 6-20.

In the earlier discussions of modified Mendelian ratios, all the crosses were dihybrid selfs. As an exercise, you might want to calculate the ratios that would be produced in the same systems if testcrosses were made instead of selfs.

A summary of some of the ratios that reveal gene interaction is shown in Table 6-2.