iga11e_ch106

Chapter 4

13.

P	A d/A d × a D/a D
F₁	A d/a D
F₂	1 A d/A d	phenotype: A d
	2 A d/a D	phenotype: A D
	1 a D/a D	phenotype: a D

16. Because only parental types are recovered, the two genes must be tightly linked and recombination must be very rare. Knowing how many progeny were looked at would give an indication of how close the genes are.

21.

The three genes are linked.
A comparison of the parentals (most frequent) with the double crossovers (least frequent) reveals that the gene order is v p b. There were 2200 recombinants between v and p, and 1500 between p and b. The general formula for map units is

m.u. = 100%(number of recombinants)/total number of progeny

Therefore, the map units between v and p = 100%(2200)/10,000 = 22 m.u., and the map units between p and b = 100%(1500)/10,000 = 15 m.u. The map is

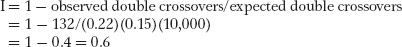
27.

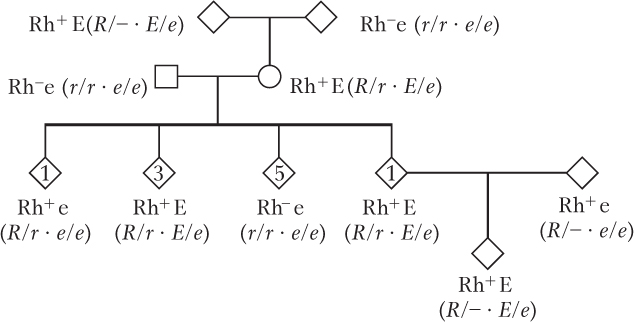
Yes.
Dominant.
As drawn, the pedigree hints at linkage. If unlinked, expect that the phenotypes of the 10 children should be in a 1 : 1 : 1 : 1 ratio of Rh⁺ E, Rh⁺ e, Rh⁻ E, and Rh⁻ e. There are actually five Rh⁻ e, four Rh⁺ E, and one Rh⁺ e. If linked, this last phenotype would represent a recombinant, and the distance between the two genes would be 100%(1/10) = 10 m.u. However, there is just not enough data to strongly support that conclusion.

33.

a. If the genes are unlinked, the cross is

P	hyg/hyg ; her/her × hyg⁺/hyg⁺ ; her⁺/her⁺
F₁	hyg⁺/hyg ; her⁺/her × hyg⁺/hyg ; her⁺/her
F₂	9/16 hyg⁺/– ; her⁺/–
	3/16 hyg⁺/– ; her/her
	3/16 hyg/hyg ; her⁺/–
	1/16 hyg/hyg ; her/her

So only 1/16 (or 6.25%) of the seeds are expected to germinate.

b. and c. No. More than twice the expected seeds germinated; so assume that the genes are linked. The cross then is

P	hyg her /hyg her × hyg⁺her⁺/hyg⁺her⁺
F₁	hyg⁺her⁺/hyg her × hyg⁺her⁺/hyg her
F₂	13% hyg her/hyg her

Because this class represents the combination of two parental chromosomes, it is equal to

p(hyg her) × p(hyg her) = (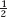 parentals)² = 0.13

and

parentals = 0.72

recombinants = 1 − 0.72 = 0.28

Therefore, a testcross of hyg⁺ hyg⁺/hyg her will give

36% hyg⁺her⁺/hyg her

36% hyg her/hyg her

14% hyg⁺her/hyg her

14% hyg her⁺/hyg her

and 36% of the progeny will grow (the hyg her/hyg her class).

37. The formula for this problem is f (i) = e⁻^mmⁱ/i! where m = 2 and i = 0, 1, or 2.

f (0) = e⁻²2⁰/0! = e⁻² = 0.135, or 13.5%
f (1) = e⁻²2¹/1! = e⁻²(2) = 0.27, or 27%
f (2) = e⁻²2²/2! = e⁻²(2) = 0.27, or 27%

43.

The cross was pro + × + his, which makes the first tetrad class NPD (6 nonparental ditypes), the second tetrad class T (82 tetratypes), and the third tetrad class PD (112 parental ditypes). When PD >> NPD, you know that the two genes are linked.

835
Map distance can be calculated by using the formula RF = [NPD + (1/2)T]100%. In this case, the frequency of NPD is 6/200, or 3%, and the frequency of T is 82/200, or 41%. Map distance between these two loci is therefore 23.5 cM.
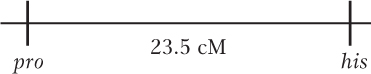
To correct for multiple crossovers, the Perkins formula can be used. Thus, map distance = (T + 6NPD)50%, or (0.41 + 0.18)50% = 29.5 cM.

47.

The cross is W e F/W e F × w E f/w E f and the F₁ are W e F/w E f. Progeny that are ww ee ff from a testcross of this F₁ must have inherited one of the double-crossover recombinant chromosomes (w e f). With the assumption of no interference, the expected percentage of double crossovers is 8% × 24% = 1.92%, half of which is 0.96%.
To obtain a ww ee ff progeny from a self cross of this F₁ requires the independent inheritance of two doubly recombinant w e f chromosomes. Its chances of happening, based on the answer to part a of this problem, are 0.96 × 0.96 = 0.009%.

53. The short answer is that the results tell us little about linkage. Although the number of recombinants (3) is less than the number of parentals (5), one can have no confidence in the fact that the RF is <50%. The main problem is that the sample size is small, so just one individual more or less in a genotypic class can dramatically affect the ratios. Even the chi-square test is unreliable at such small sample sizes. It is probably safe to say that there is not tight linkage because several recombinants were found in a relatively small sample. However, one cannot distinguish between more distant linkage and independent assortment. A larger sample size is required.

58. The data given for each of the three-point testcrosses can be used to determine the gene order when one realizes that the rarest recombinant classes are the result of double-crossover events. A comparison of these chromosomes with the “parental” types reveals that the alleles that have switched represent the gene in the middle.

For example, in data set 1, the most common phenotypes (+ + + and a b c) represent the parental-allele combinations. A comparison of these phenotypes with the rarest phenotypes of this data set (+ b c and a + +) indicates that the a gene is recombinant and must be in the middle. The gene order is b a c.

For data set 2, + b c and a + + (the parentals) should be compared with + + + and a b c (the rarest recombinants) to indicate that the a gene is in the middle. The gene order is b a c.

For data set 3, compare + b + and a + c with a b + and + + c, which gives the gene order b a c.

For data set 4, compare + + c and a b + with + + + and a b c, which gives the gene order a c b.

For data set 5, compare + + + and a b c with + + c and a b +, which gives the gene order a c b.

64.

a. Cross 1 reduces to

P	A/A · B/B · D/D × a/a · b/b · d/d
F₁	A/a · B/b · D/d × a/a · b/b · d/d

The testcross progeny indicate that these three genes are linked (CO = crossover, DCO = double crossover).

Testcross	A B D	316	parental
progeny	a b d	314	parental
	A B d	31	CO B−D
	a b D	39	CO B−D
	A b d	130	CO A−B
	a B D	140	CO A−B
	A b D	17	DCO
	a B d	13	DCO

A−B: 100%(130 + 140 + 17 + 13)/1000 = 30 m.u.

B−D: 100%(31 + 39 + 17 + 13)/1000 = 10 m.u.

Cross 2 reduces to

P	A/A ·C/C · E/E × a/a · c/c · e/e
F₁	A/a ·C/c ·E/e × a/a · c/c · e/e

The testcross progeny indicate that these three genes are linked.

Testcross	A C E	243	parental
progeny	a c e	237	parental
	A c e	62	CO A−C
	a C E	58	CO A−C
	A C e	155	CO C−E
	a c E	165	CO C−E
	a C e	46	DCO
	A c E	34	DCO

A−B: 100%(62 + 58 + 46 + 34)/1000 = 20 m.u.

B−D: 100%(155 + 165 + 46 + 34)/1000 = 40 m.u.

The map that accommodates all the data is

b Interference (I) = 1 − [(observed DCO)/(expected DCO)]

For cross 1:	I = 1 − {30/[(0.30)(0.10)(1000)]} = 1 − 1 = 0, no interference
For cross 2:	I = 1 − {80/[(0.20)(0.40)(1000)]} = 1 − 1 = 0, no interference

69. a. and b. The data support the independent assortment of two genes (call them arg1 and arg2). The cross becomes arg1 ; arg2⁺ × arg1⁺ ; arg2 and the resulting tetrads are

4 : 0 (PD)	3 : 1 (T)	2 : 2 (NPD)
arg1 ; arg2⁺	arg1 ; arg2⁺	arg1 ; arg2
arg1 ; arg2⁺	arg1⁺ ; arg2	arg1 ; arg2
arg1⁺ ; arg2	arg1 ; arg2	arg1⁺ ; arg2⁺
arg1⁺ ; arg2	arg1⁺ ; arg2⁺	arg1⁺ ; arg2⁺

Because PD = NPD, the genes are unlinked.