SOLVED PROBLEMS

1. What ratio would you expect to result if the chromosome carrying the brachytic allele does not take part in the translocation?

2. Do you think that chromosome 2 takes part in the translocation? Explain your answer, showing the conformation of the relevant chromosomes of the semisterile F₁ and the reason for the specific numbers obtained.

1. We should start with the methodical approach and simply restate the data in the form of a diagram, where

   

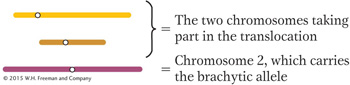
   To simplify the diagram, we do not show the chromosomes divided into chromatids (although they would be at this stage of meiosis). We then diagram the first cross:

   

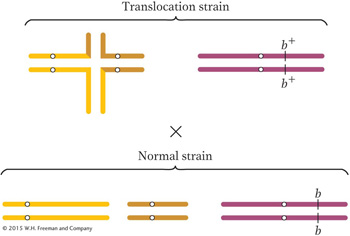
   All the progeny from this cross will be heterozygous for the chromosome carrying the brachytic allele, but what about the chromosomes taking part in the translocation? In this chapter, we have seen that only alternate-segregation products survive and that half of these survivors will be chromosomally normal and half will carry the two rearranged chromosomes. The rearranged combination will regenerate a translocation heterozygote when it combines with the chromosomally normal complement from the normal parent. These latter types—the semisterile F₁’s—are diagrammed as part of the backcross to the parental brachytic strain:

   654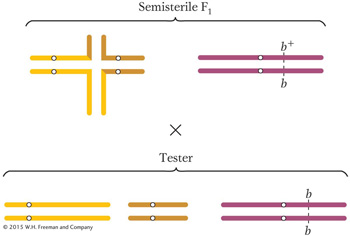

   

   In calculating the expected ratio of phenotypes from this cross, we can treat the behavior of the translocated chromosomes independently of the behavior of chromosome 2. Hence, we can predict that the progeny will be

   

   This predicted 1:1:1:1 ratio is quite different from that obtained in the actual cross.

2. Because we observe a departure from the expected ratio based on the independence of the brachytic phenotype and semisterility, chromosome 2 likely does take part in the translocation. Let’s assume that the brachytic locus (b) is on the orange chromosome. But where? For the purpose of the diagram, it doesn’t matter where we put it, but it does matter genetically because the position of the b locus affects the ratios in the progeny. If we assume that the b locus is near the tip of the piece that is translocated, we can redraw the pedigree:

   

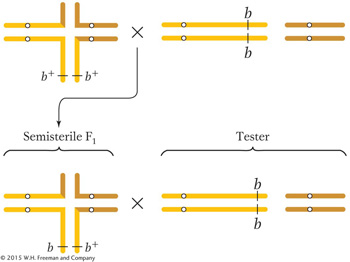
   If the chromosomes of the semisterile F₁ segregate as diagrammed here, we could then predict

   

   Most progeny are certainly of this type, and so we must be on the right track. How are the two less-frequent types produced? Somehow, we have to get the b+ allele onto the normal yellow chromosome and the b allele onto the translocated chromosome. This positioning must be achieved by crossing over between the translocation break point (the center of the cross-shaped structure) and the brachytic locus:

   

   The recombinant chromosomes produce some progeny that are fertile and nonbrachytic and some that are semisterile and brachytic (these two classes together constitute 69 progeny of a total of 682, or a frequency of about 10 percent). We can see that this frequency is really a measure of the map distance (10 m.u.) of the brachytic locus from the breakpoint. (The same basic result would have been obtained if we had drawn the brachytic locus in the part of the chromosome on the other side of the break point.)

1. A dominant allele may have mutated to a recessive allele in her normal parent.

2. In one parent, there may have been a dominant mutation in a second gene to create an epistatic allele that acts to prevent the expression of V, leading to waltzing.

3. Meiotic nondisjunction of the chromosome carrying V in her normal parent may have given a viable aneuploid.

   655

4. There may have been a viable deletion spanning V in the meiocyte from her normal parent.

   Which of these explanations are possible, and which are eliminated by the genetic analysis? Explain in detail.

1. Mutation V to v

   This hypothesis requires that the exceptional waltzer female be homozygous v/v. This assumption is compatible with the results of mating her both with waltzer males, which would, if she is v/v, produce all waltzer offspring (v/v), and with normal males, which would produce all normal offspring (V/v). However, brother–sister matings within this normal progeny should then produce a 3:1 normal-to-waltzer ratio. Because some of the brother-sister matings actually produced no waltzers, this hypothesis does not explain the data.

2. Epistatic mutation s to S

   Here the parents would be V/V · s/s and v/v · s/s, and a germinal mutation in one of them would give the F₁ waltzer the genotype V/v · S/s. When we crossed her with a waltzer male, who would be of the genotype v/v · s/s, we would expect some V/v · S/s progeny, which would be phenotypically normal. However, we saw no normal progeny from this cross, and so the hypothesis is already overthrown. Linkage could save the hypothesis temporarily if we assumed that the mutation was in the normal parent, giving a gamete V S. Then the F₁ waltzer would be VS/v s, and, if linkage were tight enough, few or no V s gametes would be produced, the type that are necessary to combine with the v s gamete from the male to give V s/v s normals. However, if the linkage hypothesis were true, the cross with the normal males would be V S/v s × V s/V s, and this would give a high percentage of V S/V s progeny, which would be waltzers, none of which were seen.

3. Nondisjunction in the normal parent

   This explanation would give a nullisomic gamete that would combine with v to give the F₁ waltzer the hemizygous genotype v. The subsequent matings would be

   •  v × v/v, which gives v/v and v progeny, all waltzers. This fits.

   •  v × V/V, which gives V/v and V progeny, all normals. This also fits.

   •  First intercrosses of normal progeny: V × V. These intercrosses give V and V/V, which are normal. This fits.

   •  Second intercrosses of normal progeny: V × V/v. These intercrosses give 25 percent each of V/V, V/v, V (all normals), and v (waltzers). This also fits.

   This hypothesis is therefore consistent with the data.

4. Deletion of V in normal parent

   Let’s call the deletion D. The F₁ waltzer would be D/v, and the subsequent matings would be

   •  D/v × v/v, which gives v/v and D/v, which are waltzers. This fits.

   •  D/v × V/V, which gives V/v and D/V, which are normal. This fits.

   •  First intercrosses of normal progeny: D/V × D/V, which give D/V and V/V, all normal. This fits.

   •  Second intercrosses of normal progeny: D/V × V/v, which give 25 percent each of V/V, V/v, D/V (all normals), and D/v (waltzers). This also fits.