SOLVED PROBLEM 1. About 70 percent of all Caucasians can taste the chemical phenylthiocarbamide, and the remainder cannot. The ability to taste this chemical is determined by the dominant allele T, and the inability to taste is determined by the recessive allele t. If the population is assumed to be in Hardy–Weinberg equilibrium, what are the genotype and allele frequencies in this population?

Solution

Because 70 percent are tasters (T/T and T/t), 30 percent must be nontasters (t/t). This homozygous recessive frequency is equal to q²; so, to obtain q, we simply take the square root of 0.30:

Because p + q = 1, we can write p = 1 − q = 1 − 0.55 = 0.45.

Now we can calculate

SOLVED PROBLEM 2. In a large experimental Drosophila population, the relative fitness of a recessive phenotype is calculated to be 0.90, and the mutation rate to the recessive allele is 5 × 10⁻⁵. If the population is allowed to come to equilibrium, what allele frequencies can be predicted?

Solution

Here, mutation and selection are working in opposite directions, and so an equilibrium is predicted. Such an equilibrium is described by the formula

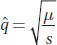
In the present question,

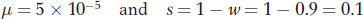
Hence,

SOLVED PROBLEM 3. A colony of 50 horned puffins (Fratercula corniculata) is established at a zoo and maintained there for 30 generations.

a. If the inbreeding coefficient of the founding members was zero (F = 0.0), what is the expected inbreeding coefficient for this population at present?

b. For a deleterious disease allele with a frequency of 0.001 in the wild, what is the predicted frequency of homozygous affected birds in the wild and in the zoo population at present?

710

Solution

a. In Box 18-3, we saw that inbreeding will increase as a function of population size (N) over time (t) as measured in generations according to the following equation:

Substituting in N = 50, t = 30, and F₀ = 0, we obtain

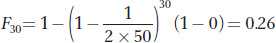
b. If the frequency of a recessive disease allele (q) in the wild is 0.001, then by applying the Hardy–Weinberg law we predict that the frequency of homozygous affected individuals in the wild will be q² = 10⁻⁶. For the zoo population, the frequency of homozygotes will be higher because of inbreeding according to the following equation:

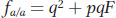
Substituting in q = 0.001, p = 0.999, and F = 0.26, we obtain

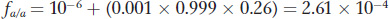
The ratio of 2.61 × 10⁻⁴ to 10⁻⁶ shows us that there is a 261-fold increase in the expected frequency of affected individuals in the current zoo population compared to the ancestral wild population.

SOLVED PROBLEM 4. At a criminal trial, the prosecutor presents genotypes for three microsatellite loci from the FBI CODIS set. He reports that a DNA sample from the crime scene and one from the suspect both have the genotype FGA₁/FGA₄, TPOX₁/TPOX₃, VWA₂/VWA₇ at these three microsatellites. He also presents the allelic frequencies for the general population to which the suspect belongs (see the table that follows). What is the probability that the genotype of the DNA evidence would match that of the suspect given that the person who committed the crime and the suspect are different individuals? What assumptions do you make when calculating this probability?

Solution

The probability that the genotype of the DNA evidence matches that of the suspect given that the person who committed the crime and the suspect are different individuals is the same as the probability that a randomly chosen member of the population would have the same genotype as the DNA evidence. The probability of a randomly chosen person being FGA₁/FGA₄ = 2pq = 2(0.30) (0.26) = 0.156 and, similarly, the probability of a random person being TPOX₁/TPOX₃ = 0.416 and VWA₂/VWA₇ = 0.2714. Applying the multiplicative rule, the probability of a random member of the population being FGA₁/FGA₄, TPOX₁/TPOX₃, VWA₂/VWA₇ = 0.156 × 0.416 × 0.2714 = 0.0176. In calculating this probability, we have assumed that the population is at Hardy–Weinberg equilibrium and that the three loci in question are at linkage equilibrium with one another.