SOLVED PROBLEMS

SOLVED PROBLEM 1. In a flock of 100 broiler chickens, the mean weight is 700 g and the standard deviation is 100 g. Assume the trait values follow the normal distribution.

  1. How many of the chickens are expected to weigh more than 700 g?

  2. How many of the chickens are expected to weigh more than 900 g?

  3. If H2 is 1.0, what is the genetic variance for this population?

Solution

  1. Since the normal distribution is symmetrical about the mean, 50 percent of the population will have a trait value above the mean and the other 50 percent will have a trait value below the mean. In this case, 50 of the 100 chickens are expected to weigh more than 700 g.

  2. The value of 900 g is 2 standard deviations greater than the mean. Under the normal distribution, 95.5 percent of the population will fall within 2 standard deviations of the mean and the remaining 4.5 percent will lie more than 2 standard deviations from the mean. Of this 4.5 percent, one-half (2.25 percent) will be more than 2 standard deviations less than the mean, and the other half (2.25 percent) will be more than 2 standard deviations greater than the mean. Thus, we expect about 2.25 percent of the 100 chickens (or roughly 2 chickens) to weigh more than 900 g.

  3. When H2 is 1.0, then all of the variance is genetic. We know that the standard deviation is 100, and the variance is the square of the standard deviation.

Variance = σ2

Thus, the genetic variance would be (100)2 = 10,000 g2.

SOLVED PROBLEM 2. Two inbred lines of beans are intercrossed. In the F1, the variance in bean weight is measured at 15 g2. The F1 is selfed; in the F2, the variance in bean weight is 61 g2. Estimate the broad heritability of bean weight in the F2 population of this experiment.

756

Solution

The key here is to recognize that all the variance in the F1 population must be environmental because all individuals have the same genotype. Furthermore, the F2 variance must be a combination of environmental and genetic components, because all the genes that are heterozygous in the F1 will segregate in the F2 to give an array of different genotypes that relate to bean weight. Hence, we can estimate

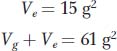
Therefore,

Vg = 61 – 15 = 46 g2

and broad heritability is

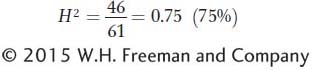
SOLVED PROBLEM 3. In an experimental population of Tribolium (flour beetles), body length shows a continuous distribution with a mean of 6 mm. A group of males and females with a mean body length of 9 mm are removed and interbred. The body lengths of their offspring average 7.2 mm. From these data, calculate the heritability in the narrow sense for body length in this population.

Solution

The selection differential (S) is 9 – 6 = 3 mm, and the selection response (R) is 7.2 – 6 = 1.2 mm. Therefore, the heritability in the narrow sense is

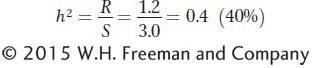
SOLVED PROBLEM 4. One research team reports that the broad-sense heritability for height in humans is 0.5 based on a study of identical twins reared apart in Iceland. Another team reports that the narrow-sense heritability for human height is 0.8 based on a study of parent–offspring correlation in the United States. What seems unexpected about these results? How could the unexpected results be explained?

Solution

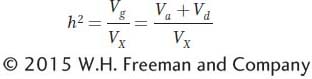
Broad-sense heritability is the ratio of the total genetic variance (Vg) to the phenotypic variance (VX). The total genetic variance includes both the additive (Va) and the dominance (Vd) variance

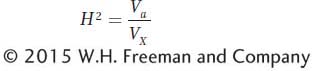
Narrow-sense heritability is the ratio of the additive variance (Va) to the phenotypic variance (VX).

Thus, all other variables being equal, H2 should be greater than or equal to h2. It will be equal to h2 when Vd is 0.0. It is unexpected that h2 should be greater than H2. However, the two research teams studied different populations—in Iceland and in the United States. Estimates of heritability apply only to the population and environment in which they were measured. Estimates made in one population can be different from those made in another population because the two populations may segregate for different alleles at numerous genes and the two populations experience different environments.