11.1 11.1 Inference for Multiple Regression
When you complete these two sections, you will be able to:
• Describe the multiple linear regression model in terms of a population regression line and the distribution of deviations of the response variable y from this line.
• Interpret statistical software regression output to obtain the least-
squares regression equation and estimated model standard deviation, multiple correlation coefficient, ANOVA F test, and individual regression coefficient t tests. • Explain the difference between the ANOVA F test and the t tests for individual coefficients.
• Interpret a level C confidence interval and a significance test for a regression coefficient.
• Use residual plots to check the assumptions of the multiple linear regression model.
Population multiple regression equation
The simple linear regression model assumes that the mean of the response variable y depends on the explanatory variable x according to a linear equation
μy = β0 + β1x
For any fixed value of x, the response y varies Normally about this mean and has a standard deviation σ that is the same for all values of x.
In the multiple regression setting, the response variable y depends on p explanatory variables, which we will denote by x1, x2, … , xp. The mean response depends on these explanatory variables according to a linear function
μy = β0 + β1x1 + β2x2 + … + βpxp
Similar to simple linear regression, this expression is the population regression equationpopulation regression equation, and the observed values y vary about their means given by this equation.
Just as we did in simple linear regression, we can also think of this model in terms of subpopulations of responses. Here, each subpopulation corresponds to a particular set of values for all the explanatory variables x1, x2, … , xp. In each subpopulation, y varies Normally with a mean given by the population regression equation. The regression model assumes that the standard deviation σ of the responses is the same in all subpopulations.
EXAMPLE 11.1
Predicting early success in college. Our case study is based on data collected on science majors at a large university.1 The purpose of the study was to attempt to predict success in the early university years. Success was measured using the cumulative grade point average (GPA) after three semesters. The explanatory variables were achievement scores available at the time of enrollment in the university. These included their average high school grades in mathematics (HSM), science (HSS), and English (HSE).
We will use high school grades to predict the response variable GPA. There are p = 3 explanatory variables: x1 = HSM, x2 = HSS, and x3 = HSE. The high school grades are coded on a scale from 1 to 10, with 10 corresponding to A, 9 to A−, 8 to B+, and so on. These grades define the subpopulations. For example, the straight-
One possible multiple regression model for the subpopulation mean GPAs is
μGPA = β0 + β1HSM + β2HSS + β3HSE
For the straight-
μGPA = β0 + β14 + β24 + β34
Data for multiple regression
The data for a simple linear regression problem consist of observations (xi, yi) of the two variables. Because there are several explanatory variables in multiple regression, the notation needed to describe the data is more elaborate. Each observation or case consists of a value for the response variable and for each of the explanatory variables. Call xij the value of the jth explanatory variable for the ith case. The data are then
Case 1: (y1, x11, x12, … , x1p)Case 2: (y2, x21, x22, … , x2p)⋮Case n: (yn, xn1, xn2, … , xnp)
Here, n is the number of cases and p is the number of explanatory variables. Data are often entered into computer regression programs in this format. Each row is a case and each column corresponds to a different variable.
The data for Example 11.1, with several additional explanatory variables, appear in this format in the GPA data file. Figure 11.1 shows the first six rows entered into an Excel spreadsheet. Grade point average (GPA) is the response variable, followed by p = 7 explanatory variables, six achievement scores and sex. There are a total of n = 150 students in this data set.
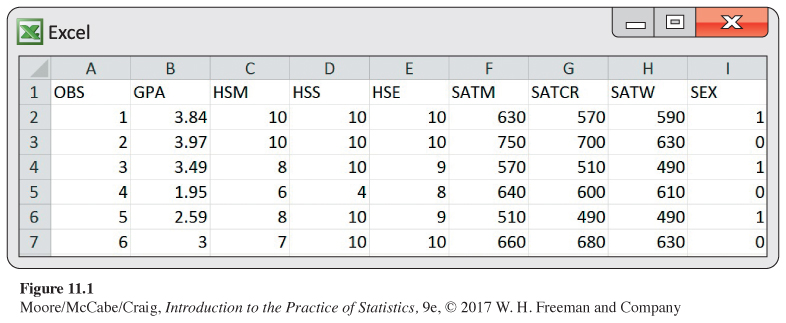
The six achievement scores are all quantitative explanatory variables. SEX is an indicator variableindicator variable using the numeric values 0 and 1 to represent male and female, respectively. Indicator variables are used frequently in multiple regression to represent the levels or groups of a categorical explanatory variable. See Exercise 11.22 (page 635) for more discussion of their use in a multiple regression model.
USE YOUR KNOWLEDGE
Question 11.1
11.1 Describing a multiple regression. To minimize the negative impact of math anxiety on achievement in a research design course, a group of researchers implemented a series of feedback sessions, in which the teacher went over the small-
(a) What is the response variable?
(b) What are the cases and what is n, the number of cases?
(c) What is p, the number of explanatory variables?
(d) What are the explanatory variables?
11.1 (a) Final exam scores. (b) 166. (c) Seven. (d) Math course anxiety, math test anxiety, numerical task anxiety, enjoyment, self-confidence, motivation, and perceived usefulness of the feedback sessions.
Multiple linear regression model
Similar to simple linear regression, we combine the population regression equation and the assumptions about how the observed y vary about their means to construct the multiple linear regression model. The subpopulation means describe the FIT part of our conceptual model
DATA = FIT + RESIDUAL
The RESIDUAL part represents the variation of observed y about their means.
We will use the same notation for the residual that we used in the simple linear regression model. The symbol ϵ represents the deviation of an individual observation from its subpopulation mean. We assume that these deviations are Normally distributed with mean 0 and an unknown model standard deviation σ that does not depend on the values of the x variables. These are assumptions that we can check by examining the residuals in the same way that we did for simple linear regression.
checking model assumptions, p. 565
MULTIPLE LINEAR REGRESSION MODEL
The statistical model for multiple linear regression is
yi=β0+β1xi1+β2xi2+⋯+βpxip+ϵi
for i = 1, 2, … , n.
The mean response μy is a linear function of the explanatory variables:
μy=β0+β1x1+β2x2+⋯+βpxp
The deviations ϵi are assumed to be independent and Normally distributed with mean 0 and standard deviation σ. In other words, they are a simple random sample (SRS) from the N(0, σ) distribution.
The parameters of the model are β0, β1, β2, … , βp, and σ.
The assumption that the subpopulation means are related to the regression coefficients β by the equation
μy=β0+β1x1+β2x2+⋯+βpxp
implies that we can estimate all subpopulation means from estimates of the β’s. To the extent that this equation is accurate, we have a useful tool for describing how the mean of y varies with the collection of x’s.
![]()
We do, however, need to be cautious when interpreting each of the regression coefficients in a multiple regression. First, the β0 coefficient represents the mean of y when all the x variables equal zero. Even more so than in simple linear regression, this subpopulation is rarely of interest. Second, the description provided by the regression coefficient of each x variable is similar to that provided by the slope in simple linear regression but only in a specific situation—
USE YOUR KNOWLEDGE
Question 11.2
11.2 Understanding the fitted regression line. The fitted regression equation for a multiple regression is
ˆy=−10.8+3.2x1+2.8x2
(a) If x1 = 4 and x2 = 2, what is the predicted value of y?
(b) For the answer to part (a) to be valid, is it necessary that the values x1 = 4 and x2 = 2 correspond to a case in the data set? Explain why or why not.
(c) If you hold x1 at a fixed value, what is the effect of an increase of three units of x2 on the predicted value of y?
least squares, p. 112
Estimation of the multiple regression parameters
Similar to simple linear regression, we use the method of least squares to obtain estimators of the regression coefficients β. Let
b0, b1, b2, … , bp
denote the estimators of the parameters
β0, β1, β2, … , βp
For the ith observation, the predicted response is
ˆyi=b0+b1xi1+b2xi2+⋯+bpxip
The ith residual, the difference between the observed and the predicted response, is, therefore,
ei= observed response−predicted response=yi−ˆyi=yi−b0−b1xi1−b2xi2−⋯−bpxip
The method of least squares chooses the values of the b’s that make the sum of the squared residuals as small as possible. In other words, the parameter estimates b0, b1, b2, … , bp minimize the quantity
Σ
![]()
The formula for the least-
The parameter σ2 measures the variability of the responses about the population regression equation. As in the case of simple linear regression, we estimate σ2 by an average of the squared residuals. The estimator is
degrees of freedom, p. 40
The quantity n − p − 1 is the degrees of freedom associated with s2. The degrees of freedom equal the sample size, n, minus (p + 1), the number of β’s we must estimate to fit the model. In the simple linear regression case, there is just one explanatory variable, so p = 1 and the degrees of freedom are n − 2. To estimate the model standard deviation σ, we use
Confidence intervals and significance tests for regression coefficients
We can obtain confidence intervals and perform significance tests for each of the regression coefficients βj as we did in simple linear regression. The standard errors of the b’s have more complicated formulas, but all are multiples of the estimated model standard deviation σ. We again rely on statistical software to do the calculations.
CONFIDENCE INTERVALS AND SIGNIFICANCE TESTS FOR βJ
A level C confidence interval for βj is
where is the standard error of bj and t* is the value for the t(n − p − 1) density curve with area C between −t* and t*.
To test the hypothesis H0: βj = 0, compute the t statistic
In terms of a random variable T having the t(n − p − 1) distribution, the P-value for a test of H0 against
Ha: βj > 0 is P(T ≥ t) 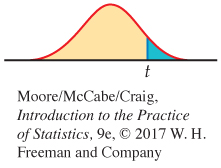
Ha: βj < 0 is P(T ≤ t) 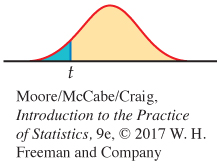
Ha: βj ≠ 0 is 2P(T ≥ |t|) 
![]()
Be very careful in your interpretation of the t tests and confidence intervals for individual regression coefficients. In simple linear regression, the model says that μy = β0 + β1x. The null hypothesis H0: β1 = 0 says that regression on x is of no value for predicting the response y or, alternatively, that there is no straight-
confidence intervals for mean response, p. 570
Because regression is often used for prediction, we may wish to use multiple regression models to construct confidence intervals for a mean response and prediction intervals for a future observation. The basic ideas are the same as in the simple linear regression case.
In most software systems, the same commands that give confidence and prediction intervals for simple linear regression work for multiple regression. The only difference is that we specify a list of explanatory variables rather than a single variable. Modern software allows us to perform these rather complex calculations without an intimate knowledge of all the computational details. This frees us to concentrate on the meaning and appropriate use of the results.
ANOVA table for multiple regression
ANOVA F test, p. 586
In simple linear regression, the F test from the ANOVA table is equivalent to the two-
| Source | Degrees of freedom | Sum of squares | Mean square | F |
|---|---|---|---|---|
| Model | p | SSM/DFM | MSM/MSE | |
| Error | n − p − 1 | SSE/DFE | ||
| Total | n − 1 | SST/DFT |
![]()
The ANOVA table is similar to that for simple linear regression. The degrees of freedom for the model increase from 1 to p to reflect the fact that we now have p explanatory variables rather than just one. As a consequence, the degrees of freedom for error decrease by the same amount. It is always a good idea to calculate the degrees of freedom by hand and then check that your software agrees with your calculations. This ensures that you have not made some serious error in specifying the model or in entering the data.
The sums of squares represent sources of variation. Once again, both the sums of squares and their degrees of freedom add:
SST = SSM + SSE
DFT = DFM + DFE
F statistic, p. 585
The estimate of the variance σ2 for our model is again given by the MSE in the ANOVA table. That is, s2 = MSE.
The ratio MSM/MSE is an F statistic for testing the null hypothesis
H0: β1 = β2 = … = βp = 0
against the alternative hypothesis
Ha: at least one of the βj is not 0
The null hypothesis says that none of the explanatory variables are predictors of the response variable when used in the form expressed by the multiple regression equation. The alternative states that at least one of them is a predictor of the response variable.
As in simple linear regression, large values of F give evidence against H0. When H0 is true, F has the F(p, n − p − 1) distribution. The degrees of freedom for the F distribution are those associated with the model and error in the ANOVA table.
ANALYSIS OF VARIANCE F TEST
In the multiple regression model, the hypothesis
H0: β1 = β2 = … = βp = 0
is tested against the alternative hypothesis
Ha: at least one of the βj is not 0
by the analysis of variance F statistic
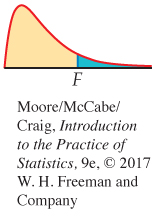
The P-value is the probability that a random variable having the F(p, n − p − 1) distribution is greater than or equal to the calculated value of the F statistic.
![]()
A common error in the use of multiple regression is to assume that all the regression coefficients are statistically different from zero whenever the F statistic has a small P-value. Be sure that you understand the difference between the F test and the t tests for individual coefficients in the multiple regression setting.
r2 in regression p. 116
Squared multiple correlation R2
For simple linear regression, we noted that the square of the sample correlation could be written as the ratio of SSM to SST and could be interpreted as the proportion of variation in y explained by x. The ratio of SSM to SST is routinely calculated for multiple regression and still can be interpreted as the proportion of explained variation. The difference is that it relates to the collection of explanatory variables in the model.
THE SQUARED MULTIPLE CORRELATION
The statistic
is the proportion of the variation of the response variable y that is explained by the explanatory variables x1, x2, … , xp in a multiple linear regression.
Often, R2 is multiplied by 100 and expressed as a percent. The square root of R2, called the multiple correlation coefficientmultiple correlation coefficient, is the correlation between the observations yi and the predicted values