3.3 3.3 Sampling Design
When you complete this section, you will be able to:
• Distinguish between a population and a sample.
• Use the response rate to evaluate a survey.
• Use Table B to generate a simple random sample (SRS).
• Use software to generate a simple random sample.
• Construct a stratified random sample using Table B or software to select the samples from the strata.
• Identify voluntary response samples, simple random samples, stratified random samples, and multistage random samples.
• Identify characteristics of samples that limit their usefulness, including undercoverage, nonresponse, response bias, and the wording of questions.
A political scientist wants to know what percent of college-age adults consider themselves conservatives. An automaker hires a market research firm to learn what percent of adults aged 18 to 35 recall seeing television advertisements for a new sports utility vehicle. Government economists inquire about average household income.
In all these cases, we want to gather information about a large group of individuals. We will not, as in an experiment, impose a treatment in order to observe the response. Also, time, cost, and inconvenience forbid contacting every individual. In such cases, we gather information about only part of the group—a sample—in order to draw conclusions about the whole. Sample surveyssample survey are an important kind of observational study.
POPULATION AND SAMPLE
The entire group of individuals that we want information about is called the population.
A sample is a part of the population that we actually examine in order to gather information.
Notice that “population” is defined in terms of our desire for knowledge. If we wish to draw conclusions about all U.S. college students, that group is our population even if only local students are available for questioning. The sample is the part from which we draw conclusions about the whole. The design of a sample surveysample design refers to the method used to choose the sample from the population.
EXAMPLE 3.21

The Reading Recovery program. The Reading Recovery (RR) program has specially trained teachers work one-on-one with at-risk first-grade students to help them learn to read. A study was designed to examine the relationship between the RR teachers’ beliefs about their ability to motivate students and the progress of the students whom they teach.13 The Reading Recovery International Data Evaluation Center website (www.idecweb.us) says that there are 13,823 RR teachers. The researchers send a questionnaire to a random sample of 200 of these. The population consists of all 13,823 RR teachers, and the sample is the 200 that were randomly selected.
Unfortunately, our idealized framework of population and sample does not exactly correspond to the situations that we face in many cases. In Example 3.21, the list of teachers was prepared at a particular time in the past. It is very likely that some of the teachers on the list are no longer working as RR teachers today. New teachers have been trained in RR methods and are not on the list. Despite these difficulties, we still view the list as the population. Also, we may have out-of-date addresses for some who are still working as RR teachers, and some teachers may choose not to respond to the survey questions.
In reporting the results of a sample survey, it is important to include all details regarding the procedures used. Follow-up mailings or phone calls to those who do not initially respond can help increase the response rate. The proportion of the original sample who actually provide usable data is called the response rateresponse rate and should be reported for all surveys. If only 150 of the teachers who were sent questionnaires provided usable data, the response rate would be 150/200, or 75%.
USE YOUR KNOWLEDGE
Question 3.44
3.44 Are they satisfied? An educational research team wanted to examine the relationship between faculty participation in decision making and job satisfaction in Mongolian public universities. They are planning to randomly select 250 faculty members from a list of 2000 faculty members in these universities. The Job Descriptive Index will be used to measure job satisfaction, and the Conway Adaptation of the Alutto-Belasco Decisional Participation Scale will be used to measure decision participation.
- Page 190
(a) Describe the population for this study.
(b) Describe the sample for this study.
(c) How would you determine the response rate for this study? Can you calculate it from the information given? If your answer is yes, calculate it.
Question 3.45
3.45 What is the impact of the taxes? A study was designed to assess the impact of taxes on forest land usage in part of the Upper Wabash River Watershed in Indiana.14 A survey was sent to 772 forest owners from this region, and 348 were returned.
(a) What is the sample for this study?
(b) What is the population for this study?
(c) How would you determine the response rate for this study? Can you calculate it from the information given? If your answer is yes, calculate it.
3.45 (a) The sample is the 772 forest owners that the survey was sent to. (b) The population is all forest owners from this region. (c) The response rate is the percentage of those who were sent the survey who returned it: 45%.
Poor sample designs can produce misleading conclusions. Here is an example.
EXAMPLE 3.22
Sampling pieces of steel. A mill produces large coils of thin steel for use in manufacturing home appliances. The quality engineer wants to submit a sample of 5-centimeter squares to detailed laboratory examination. She asks a technician to cut a sample of 10 such squares. Wanting to provide “good” pieces of steel, the technician carefully avoids the visible defects in the coil material when cutting the sample. The laboratory results are wonderful, but the customers complain about the material they are receiving.
bias, p. 74
In Example 3.22, the sample was selected in a manner that guaranteed that it would not be representative of the entire population. This sampling scheme displays bias, or systematic error, in favoring some parts of the population over others.
Online polls use voluntary response samples, a particularly common form of biased sample. The sample who respond are not representative of the population at large. People who take the trouble to respond to an open invitation are not representative of the entire population.
VOLUNTARY RESPONSE SAMPLE
A voluntary response sample consists of people who choose themselves by responding to a general appeal. Voluntary response samples are biased because people with strong opinions, especially negative opinions, are most likely to respond.
The remedy for bias in choosing a sample is to allow chance to do the choosing so that there is neither favoritism by the sampler (Example 3.22) nor voluntary response (online opinion polls). Random selection of a sample eliminates bias by giving all individuals an equal chance to be chosen, just as randomization eliminates bias in assigning experimental units.
Simple random samples
The simplest sampling design amounts to placing names in a hat (the population) and drawing out a handful (the sample). This is simple random sampling.
SIMPLE RANDOM SAMPLE
A simple random sample (SRS) of size n consists of n individuals from the population chosen in such a way that every set of n individuals has an equal chance to be the sample actually selected.
Each treatment group in a completely randomized experimental design is an SRS drawn from the available experimental units. We select an SRS by labeling all the individuals in the population and using software or a table of random digits to select a sample of the desired size, just as in experimental randomization. Notice that an SRS not only gives every possible sample an equal chance to be chosen, but also gives each individual an equal chance to be chosen. There are other random sampling designs that give each individual, but not each sample, an equal chance. One such design, systematic random sampling, is described in Exercise 3.64 (page 202).
How to select a simple random sample
The basic ideas needed to select a simple random sample are very similar to those that we discussed when we randomized subjects to treatments (page 177). We first assign a label to each case in our population. Then we perform the randomization using software or random digits from Table B.
Selection of a simple random sample using software The World Bank collects information about starting businesses throughout the world. In Example 1.23 (page 26) and several other examples in Chapter 1, we examined the time to start a business in a subset of these countries. For those exercises, we used a subset of the data because it was easier to show some details about our calculations with a smaller amount of data.
Now, suppose we want to collect additional information about countries that would help us to understand the processes of starting a business. The complete data set contains entries for 189 countries, and the time required to collect the additional information on all these would be too much. Let’s use Excel to select a sample of 25 countries for a more detailed examination of these countries.
EXAMPLE 3.23
Select an SRS of countries using Excel. The data file TTS includes columns for the country name and a three-letter country code for each of the 189 countries. We could use either of these for our label. We will use the three letter codes in our screen shots to save space.
Figure 3.7(a) shows the codes for the first ten countries. In Figure 3.7(b), we show the uniform numbers generated with the RAND() function (and then pasted into column C). The first three countries are Afghanistan (AFG), Angola (AGO), and Albania (ALB).
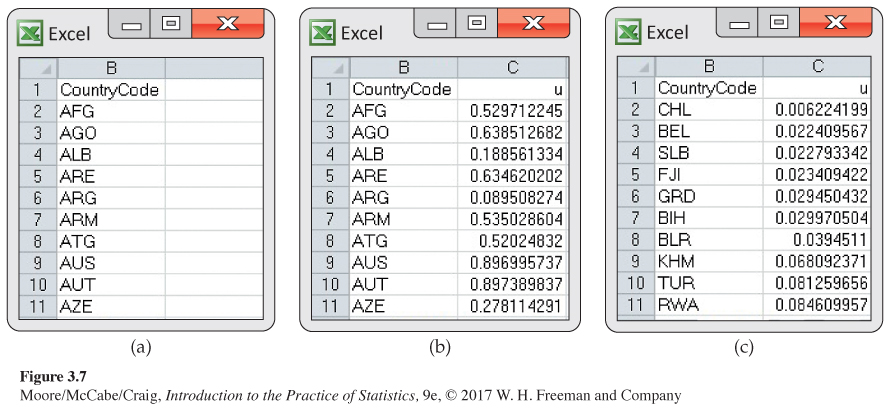
Figure 3.7(c) shows the file after we sort on the uniform random numbers in column C. Our sample is the first 25 countries in the sorted file. The first three selected are Chile (CHL), Belgium (BEL), and the Solomon Islands (SLB). Note that Excel does not display the last two digits for Belarus (BLR) because they are zero.
The Simple Random Sample applet on the text website is another convenient way to select an SRS.
USE YOUR KNOWLEDGE
Question 3.46
3.46 Select an SRS. Use the Simple Random Sample applet or Excel to select an SRS of five countries from the TTS data file. Include a step-by-step detailed description of how you selected the countries.
Selection of a simple random sample using random digits We illustrate the procedure by selecting an SRS of countries from the population of 189 countries in the data file TTS. Recall that we used Excel to select such a sample in Example 3.23.
EXAMPLE 3.24
Select an SRS of countries using random digits. To use Table B, we need a numeric label. We could create such a label by adding a column to the data file TTS containing the numbers 1 to 189. An alternative requiring less work would be to use the numbers in the leftmost part of the spreadsheet. Notice in Figure 3.7(a), for example, that there is a 1 in the first row of the spreadsheet where we have entered the names of the variables in the columns. Therefore, the numbers corresponding to countries run from 2 through 190. We will use these numbers as our label.
We will examine the entries in Table B in sets of three. Three digit numbers between 2 and 190 will correspond to selected countries. We will ignore three digit numbers equal to 000, 001, or greater than 190. Let’s start our selection at line 106 in Table B. The entries on this line are
68417 35013 15529 72765 85089 57067 50211 47487
If we arrange these into sets of three, we have
684 173 501 315 529 727 658 508 057 067 502 114 748 7
The selected labels from this set of random digits are 173, 057, and 067. Checking the spreadsheet, we see that these numbers correspond to Turkey, France, and Greece.
Note that we do not use the last digit on line 106 to select the country with the label 7. We should combine this single digit with the first two digits from line 107 of Table B. This gives us the three-digit number 782, which is a number that we ignore. We complete our selection of the additional 22 countries that we need in our SRS using additional lines from Table B as needed.
USE YOUR KNOWLEDGE
Question 3.47
3.47 Find the next three countries to be selected. Continue the process described in Example 3.24 to select the next three countries for the SRS. Show your work.
3.47 The next three labels selected are 114, 080, 094. These correspond to Malta, Iraq, and Kosovo.
Question 3.48
3.48 Listen to three rock songs. The walk to your statistics class takes about 10 minutes, about the amount of time needed to listen to three songs on your iPod or smartphone. You decide to take a simple random sample of songs from the top 10 listed on a Billboard Hot Rock Songs.15 Here is the list:
| Shut Up and Dance |
Uma Thurman | Renegades | Ex’s & Oh’s |
| Centuries | Cecilia and the Satellite |
Tear in My Heart |
Brother |
| Stressed Out | Shots |
Select your three hot rock songs using a simple random sample. Show your work.
Question 3.49
3.49 Listen to three songs. Refer to the previous exercise. Suppose that you like to include more variety in your music, so you look at the Billboard Top 100 songs.16 Here are the top 10 on this list:
| Cheerleader | Can’t Feel My Face | Watch Me | Lean On |
| The Hills | Good for You | Fight Song | 679 |
| Trap Queen | Shut Up and Dance |
Select the three songs for your iPod or smartphone using a simple random sample. Show your work.
EXAMPLE 3.25
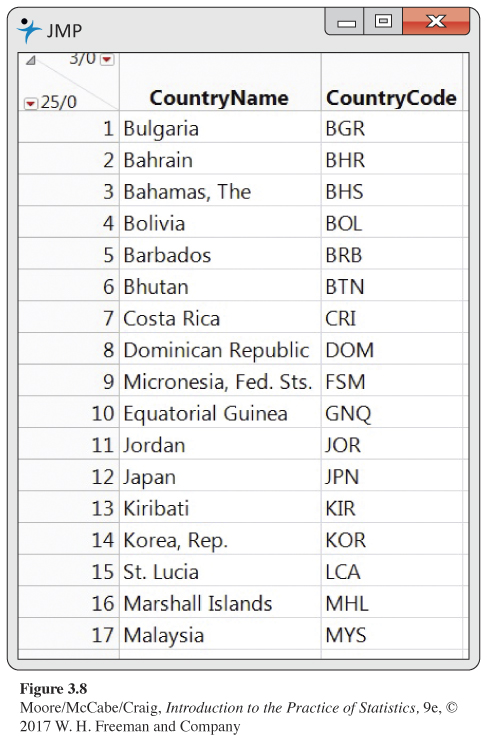
Select an SRS of countries using JMP. Refer to Example 3.23, where we selected an SRS of countries from a population of 189 countries. Also see Example 3.24, where we used the random digits in Table B to select the SRS. We can also use JMP to select an SRS. The output for the first 17 countries selected is displayed in Figure 3.8. JMP provides a file with the selected countries with all columns in the original data file. Note that the selected files are listed in the order that they appear in the original file, which is alphabetically in this case.
Stratified random samples
The general framework for designs that use chance to choose a sample is a probability sample.
PROBABILITY SAMPLE
A probability sample is a sample chosen by chance. We must know what samples are possible and what chance, or probability, each possible sample has.
Some probability sampling designs (such as an SRS) give each member of the population an equal chance to be selected. This may not be true in more elaborate sampling designs. In every case, however, the use of chance to select the sample is the essential principle of statistical sampling.
Designs for sampling from large populations spread out over a wide area are usually more complex than an SRS. For example, it is common to sample important groups within the population separately, then combine these samples. This is the idea of a stratified sample.
STRATIFIED RANDOM SAMPLE
To select a stratified random sample, first divide the population into groups of similar individuals, called strata. Then choose a separate SRS in each stratum and combine these SRSs to form the full sample.
Choose the strata based on facts known before the sample is taken. For example, a population of election districts might be divided into urban, suburban, and rural strata.
A stratified design can produce more exact information than an SRS of the same size by taking advantage of the fact that individuals in the same stratum are similar to one another. Think of the extreme case in which all individuals in each stratum are identical: just one individual from each stratum is then enough to completely describe the population.
Strata for sampling are similar to blocks in experiments. We have two names because the idea of grouping similar units before randomizing arose separately in sampling and in experiments.
EXAMPLE 3.26
A stratified sample of countries. In Examples 3.23 and 3.24, we selected SRSs of size 25 from the population of 189 countries in the World Bank file with data on starting businesses. Let’s think about using a stratified sample. You still want to select 25 companies to examine in detail.
Let’s classify each of the countries as located in Asia, Africa, Europe, North or South America, and Other. We have five strata, and we want a total of 25 countries to examine in detail. Therefore, we need to sample five countries from each stratum. We take an SRS of size 5 from each of these strata.
Multistage random samples
Another common means of restricting random selection is to choose the sample in stages. These designs are called multistage designsmultistage random sample. They are widely used in national samples of households or people. For example, data on employment and unemployment are gathered by the government’s Current Population Survey, which conducts interviews in about 60,000 households each month. The cost of sending interviewers to the widely scattered households in an SRS would be too high. Moreover, the government wants data broken down by states and large cities.
Thus, the Current Population Survey uses a multistage random sampling design. The final sample consists of groups of nearby households, called clustersclusters, that an interviewer can easily visit. Most opinion polls and other national samples are also multistage, though interviewing in most national samples today is done by telephone rather than in person, eliminating the economic need for clustering. The Current Population Survey sampling design is roughly as follows:17
Stage 1. Divide the United States into 2007 geographical areas called Primary Sampling Units, or PSUs. PSUs do not cross state lines. Select a sample of 754 PSUs. This sample includes the 428 PSUs with the largest population and a stratified sample of 326 of the others.
Stage 2. Divide each PSU selected into smaller areas called “blocks.” Stratify the blocks using ethnic and other information, and take a stratified sample of the blocks in each PSU.
Stage 3. Sort the housing units in each block into clusters of four nearby units. Interview the households in a probability sample of these clusters.
Analysis of data from sampling designs more complex than an SRS takes us beyond basic statistics. But the SRS is the building block of more elaborate designs, and analysis of other designs differs more in complexity of detail than in fundamental concepts.
Cautions about sample surveys
Random selection eliminates bias in the choice of a sample from a list of the population. Sample surveys of large human populations, however, require much more than a good sampling design.18 To begin, we need an accurate and complete list of the population. Because such a list is rarely available, most samples suffer from some degree of undercoverage. A sample survey of households, for example, will miss not only homeless people, but also prison inmates and students in dormitories. An opinion poll conducted by telephone will miss the large number of American households without residential phones. The results of national sample surveys, therefore, have some bias if the people not covered—who most often are poor people—differ from the rest of the population.
A more serious source of bias in most sample surveys is nonresponse, which occurs when a selected individual cannot be contacted or refuses to cooperate. Nonresponse to sample surveys often reaches 50% or more, even with careful planning and several callbacks. Because nonresponse is higher in urban areas, most sample surveys substitute other people in the same area to avoid favoring rural areas in the final sample. If the people contacted differ from those who are rarely at home or who refuse to answer questions, some bias remains.
UNDERCOVERAGE AND NONRESPONSE
Undercoverage occurs when some groups in the population are left out of the process of choosing the sample.
Nonresponse occurs when an individual chosen for the sample can’t be contacted or does not cooperate.
EXAMPLE 3.27
Nonresponse in the Current Population Survey. How bad is nonresponse? The Current Population Survey (CPS) has the lowest nonresponse rate of any poll we know: only about 5% of the households in the CPS sample refuse to take part, and another 2% or 3% can’t be contacted.19 People are more likely to respond to a government survey such as the CPS, and the CPS contacts its sample in person before doing later interviews by phone.
The General Social Survey (Figure 3.9) is the nation’s most important social science research survey. The GSS also contacts its sample in person, and it is run by a university. Despite these advantages, its most recent survey had a 30% rate of nonresponse.20

What about polls done by the media and by market research and opinion-polling firms? Often, we don’t know their rates of nonresponse because they won’t say. That itself is a bad sign.
EXAMPLE 3.28
Change in nonresponse in Pew surveys. The Pew Research Center conducts research using surveys on a variety of issues, attitudes, and trends.21 A study by the center examined the decline in the response rates to their surveys over time. The changes are dramatic, and there is a consistent pattern over time. Here are some data from the report:22
| Year | 1997 | 2000 | 2003 | 2006 | 2009 | 2012 |
| Nonresponse rate | 64% | 72% | 75% | 79% | 85% | 91% |
The center is devising alternative methods that show some promise of improving the response rates of their surveys.
Most sample surveys, and almost all opinion polls, are now carried out by telephone. This and other details of the interview method can affect the results. When presented with several options for a reply, such as “completely agree,” “mostly agree,” “mostly disagree,” and “completely disagree,” people tend to be a little more likely to respond to the first one or two options presented.
The behavior of the respondent or of the interviewer can cause response biasresponse bias in sample results. Respondents may lie, especially if asked about illegal or unpopular behavior. The race or sex of the interviewer can influence responses to questions about race relations or attitudes toward feminism. Answers to questions that ask respondents to recall past events are often inaccurate because of faulty memory. For example, many people “telescope” events in the past, bringing them forward in memory to more recent time periods. “Have you visited a dentist in the last six months?” will often elicit a Yes from someone who last visited a dentist eight months ago.
The wording of questionswording of questions is the most important influence on the answers given to a sample survey. Confusing or leading questions can introduce strong bias, and even minor changes in wording can change a survey’s outcome. Here are some examples.
EXAMPLE 3.29
The form of the question is important. In response to the question “Are you heterosexual, homosexual, or bisexual?” in a social science research survey, one woman answered, “It’s just me and my husband, so bisexual.” The issue is serious, even if the example seems silly: reporting about sexual behavior is difficult because people understand and misunderstand sexual terms in many ways.
How do Americans feel about government help for the poor? Only 13% think we are spending too much on “assistance to the poor,” but 44% think we are spending too much on “welfare.” How do the Scots feel about the movement to become independent from England? Well, 51% would vote for “independence for Scotland,” but only 34% support “an independent Scotland separate from the United Kingdom.” It seems that “assistance to the poor” and “independence” are nice, hopeful words. “Welfare” and “separate” are negative words.23
![]()
The statistical design of sample surveys is a science, but this science is only part of the art of sampling. Because of nonresponse, response bias, and the difficulty of posing clear and neutral questions, you should hesitate to fully trust reports about complicated issues based on surveys of large human populations. Insist on knowing the exact questions asked, the rate of nonresponse, and the date and method of the survey before you trust a poll result.
BEYOND THE BASICS
Capture-Recapture Sampling
Sockeye salmon return to reproduce in the river where they were hatched four years earlier. How many salmon survived natural perils and heavy fishing to make it back this year? How many mountain sheep are there in Colorado? Are migratory songbird populations in North America decreasing or holding their own? These questions concern the size of animal populations. Biologists address them with a special kind of repeated sampling, called capture-recapture sampling.
EXAMPLE 3.30
Estimate the number of least flycatchers. You are interested in the number of least flycatchers migrating along a major route in the north-central United States. You set up “mist nets” that capture the birds but do not harm them. The birds caught in the net are fitted with a small aluminum leg band and released. Last year, you banded and released 200 least flycatchers. This year, you repeat the process. Your net catches 120 least flycatchers, 12 of which have tags from last year’s catch.

The proportion of your second sample that have bands should estimate the proportion in the entire population that are banded. So if N is the unknown number of least flycatchers, we should have approximately
proportion banded in sample=proportion banded in population12120=200N
Solve for N to estimate that the total number of flycatchers migrating while your net was up this year is approximately
N=200×12012=2000
The capture-recapture idea extends the use of a sample proportion to estimate a population proportion. The idea works well if both samples are SRSs from the population and the population remains unchanged between samples. In practice, complications arise because, for example, some of the birds tagged last year died before this year’s migration.
Variations on capture-recapture samples are widely used in wildlife studies and are now finding other applications. One way to estimate the census undercount in a district is to consider the census as “capturing and marking” the households that respond. Census workers then visit the district, take an SRS of households, and see how many of those counted by the census show up in the sample. Capture-recapture estimates the total count of households in the district. As with estimating wildlife populations, there are many practical pitfalls. Our final word is as before: the real world is less orderly than statistics textbooks imply.