The story of the boom and bust in Ft. Myers involves a sort of chain reaction in which an initial rise or fall in spending leads to changes in income, which lead to further changes in spending, and so on. Let’s examine that chain reaction more closely, this time thinking through the effects of changes in spending on the economy as a whole.

For the sake of this analysis, we’ll make the following four simplifying assumptions that we will have to reconsider in later modules:

Given these simplifying assumptions, consider what happens if there is a change in investment spending. Specifically, imagine that for some reason home builders decide to spend an extra $100 billion on home construction over the next year.

160

The direct effect of this increase in investment spending will be to increase income and the value of aggregate output by the same amount. That’s because each dollar spent on home construction translates into a dollar’s worth of income for construction workers, suppliers of building materials, electricians, and so on. If the process stopped there, the increase in residential investment spending would raise overall income by exactly $100 billion.

But the process doesn’t stop there. The increase in aggregate output leads to an increase in disposable income that flows to households in the form of profits and wages. The increase in households’ disposable income leads to a rise in consumer spending, which, in turn, induces firms to increase output yet again. This generates another rise in disposable income, which leads to another round of consumer spending increases, and so on. So there are multiple rounds of increases in aggregate output.

How large is the total effect on aggregate output if we sum the effect from all these rounds of spending increases? To answer this question, we need to introduce the concept of the marginal propensity to consume, or MPC: the increase in consumer spending when disposable income rises by $1. When consumer spending changes because of a rise or fall in disposable income, MPC is the change in consumer spending divided by the change in disposable income:

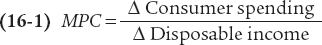
where the symbol Δ (delta) means “change in.” For example, if consumer spending goes up by $6 billion when disposable income goes up by $10 billion, MPC is $6 billion/$10 billion = 0.6.

Because consumers normally spend part but not all of an additional dollar of disposable income, MPC is a number between 0 and 1. The additional disposable income that consumers don’t spend is saved; the marginal propensity to save, or MPS, is the fraction of b an additional $1 of disposable income that is saved. MPS is equal to 1 - MPC.

With the assumption of no taxes and no international trade, each $1 increase in spending raises both real GDP and disposable income by $1. So the $100 billion increase in investment spending initially raises real GDP by $100 billion. The corresponding $100 billion increase in disposable income leads to a second-round increase in consumer spending, which raises real GDP by a further MPC × $100 billion. It is followed by a third-round increase in consumer spending of MPC × MPC × $100 billion, and so on. After an infinite number of rounds, the total effect on real GDP is:

So the $100 billion increase in investment spending sets off a chain reaction in the economy. The net result of this chain reaction is that a $100 billion increase in investment spending leads to a change in real GDP that is a multiple of the size of that initial change in spending.

How large is this multiple? It’s a mathematical fact that an infinite series of the form 1 + x + x² + x³ + . . ., where x is between 0 and 1, is equal to 1/(1 − x). So the total effect of a $100 billion increase in investment spending, I, taking into account all the subsequent increases in consumer spending (and assuming no taxes and no international trade), is given by:

161

(16-2) Total increase in real GDP from $100 billion rise in

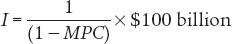
Let’s consider a numerical example in which MPC = 0.6: each $1 in additional disposable income causes a $0.60 rise in consumer spending. In that case, a $100 billion increase in investment spending raises real GDP by $100 billion in the first round. The second-round increase in consumer spending raises real GDP by another 0.6 × $100 billion, or $60 billion. The third-round increase in consumer spending raises real GDP by another 0.6 × $60 billion, or $36 billion. This process goes on and on until the amount of spending in another round would be virtually zero. In the end, real GDP rises by $250 billion as a consequence of the initial $100 billion rise in investment spending:

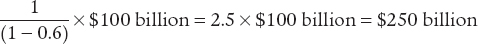
Notice that even though there can be a nearly endless number of rounds of expansion of real GDP, the total rise in real GDP is limited to $250 billion. The reason is that at each stage some of the rise in disposable income “leaks out” because it is saved, leaving less and less to be spent in the next round. How much of an additional dollar of disposable income is saved depends on MPS, the marginal propensity to save.

We’ve described the effects of a change in investment spending, but the same analysis can be applied to any other change in spending. The important thing is to distinguish between the initial change in aggregate spending, before real GDP rises, and the additional change in aggregate spending caused by the change in real GDP as the chain reaction unfolds. For example, suppose that a boom in housing prices makes consumers feel richer and that, as a result, they become willing to spend more at any given level of disposable income. This will lead to an initial rise in consumer spending, before real GDP rises. But it will also lead to second and later rounds of higher consumer spending as real GDP and disposable income rise.

An initial rise or fall in aggregate spending at a given level of real GDP is called an autonomous change in aggregate spending. It’s autonomous—which means “self-governing”—because it’s the cause, not the result, of the chain reaction we’ve just described. Formally, the spending multiplier is the ratio of the total change in real GDP caused by an autonomous change in aggregate spending to the size of that autonomous change. If we let ΔAAS stand for the autonomous change in aggregate spending and ΔY stand for the total change in real GDP, then the spending multiplier is equal to ΔY/ΔAAS. We’ve already seen how to find the value of the spending multiplier. Assuming no taxes and no trade, the total change in real GDP caused by an autonomous change in aggregate spending is:

So the spending multiplier is:

Notice that the size of the spending multiplier depends on MPC. If the marginal propensity to consume is high, so is the spending multiplier. This is true because the size of MPC determines how large each round of expansion is compared with the previous round. To put it another way, the higher MPC is, the less disposable income “leaks out” into savings at each round of expansion.

162

In later modules we’ll use the concept of the spending multiplier to analyze the effects of fiscal and monetary policies. We’ll also see that the spending multiplier changes when we introduce various complications, including taxes and foreign trade. First, however, we need to look more deeply at what determines consumer spending.