When a government is considering whether to impose a tax or how to design a tax system, it has to weigh the benefits of a tax against its costs. We may not think of a tax as something that provides benefits, but governments need money to provide things people want, such as streets, schools, national defense, and health care for those unable to afford it. The benefit of a tax is the revenue it raises for the government to pay for these services. Unfortunately, this benefit comes at a cost—a cost that is normally larger than the amount consumers and producers pay. Let’s look first at what determines how much money a tax raises and then at the costs a tax imposes.

How much revenue does the government collect from an excise tax? In our hotel tax example, the revenue is equal to the area of the shaded rectangle in Figure 50.10.

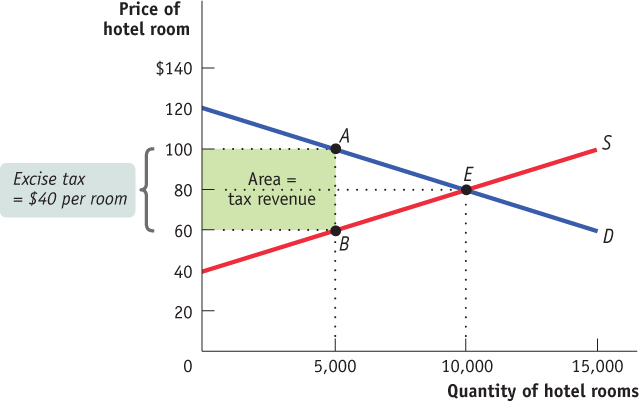
To see why this area represents the revenue collected by a $40 tax on hotel rooms, notice that the height of the rectangle is $40, equal to the tax per room. As we've seen, it is also the size of the wedge that the tax drives between the supply price (the price received by producers) and the demand price (the price paid by consumers). Meanwhile, the width of the rectangle is 5,000 rooms, equal to the equilibrium quantity of rooms given the $40 tax. With that information, we can make the following calculations.

509

The tax revenue collected is:

Tax revenue = $40 per room × 5,000 rooms = $200,000

The area of the shaded rectangle is:

Area = Height × Width = $40 per room × 5,000 rooms = $200,000,

or

Tax revenue = Area of shaded rectangle

This is a general principle: The revenue collected by an excise tax is equal to the area of a rectangle with the height of the tax wedge between the supply price and the demand price and the width of the quantity sold under the tax.

What is the cost of a tax? You might be inclined to answer that it is the amount of money taxpayers pay to the government—the tax revenue collected. But suppose the government uses the tax revenue to provide services that taxpayers want. Or suppose that the government simply hands the tax revenue back to taxpayers. Would we say in those cases that the tax didn’t actually cost anything?

No—because a tax, like a quota, prevents mutually beneficial transactions from occurring. Consider Figure 50.10 once more. Here, with a $40 tax on hotel rooms, guests pay $100 per room but hotel owners receive only $60 per room. Because of the wedge created by the tax, we know that some transactions didn’t occur that would have occurred without the tax. More specifically, we know from the supply and demand curves that there are some potential guests who would be willing to pay up to $90 per night and some hotel owners who would be willing to supply rooms if they received at least $70 per night. If these two sets of people were allowed to trade with each other without the tax, they would engage in mutually beneficial transactions—hotel rooms would be rented. But such deals would be illegal because the $40 tax would not be paid. In our example, 5,000 potential hotel room rentals that would have occurred in the absence of the tax, to the mutual benefit of guests and hotel owners, do not take place because of the tax.

So an excise tax imposes costs over and above the tax revenue collected in the form of inefficiency, which occurs because the tax discourages mutually beneficial transactions. You may recall from Module 9 that the cost to society of this kind of inefficiency—the value of the forgone mutually beneficial transactions—is called the deadweight loss. While most real-world taxes impose some deadweight loss, a badly designed tax imposes a larger deadweight loss than a well-designed one.

To measure the deadweight loss from a tax, we turn to the concepts of producer and consumer surplus. Figure 50.11 shows the effects of an excise tax on consumer and producer surplus. In the absence of the tax, the equilibrium is at E and the equilibrium price and quantity are P_E and Q_E, respectively. An excise tax drives a wedge equal to the amount of the tax between the price received by producers and the price paid by consumers, reducing the quantity sold. In this case, with a tax of T dollars per unit, the quantity sold falls to Q_T. The price paid by consumers rises to P_C, the demand price of the reduced quantity, Q_T, and the price received by producers falls to P_P, the supply price of that quantity. The difference between these prices, P_C – P_P, is equal to the excise tax, T.

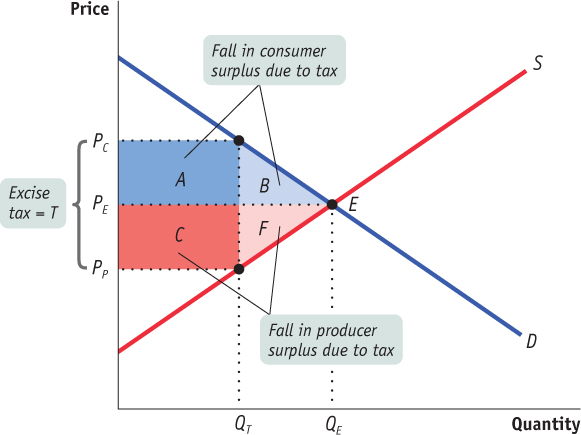
Using the concepts of producer and consumer surplus, we can show exactly how much surplus producers and consumers lose as a result of the tax. We learned previously that a fall in the price of a good generates a gain in consumer surplus that is equal to the sum of the areas of a rectangle and a triangle. Similarly, a price increase causes a loss to consumers that is represented by the sum of the areas of a rectangle and a triangle. So it’s not surprising that in the case of an excise tax, the rise in the price paid by consumers causes a loss equal to the sum of the areas of a rectangle and a triangle: the dark blue rectangle labeled A and the area of the light blue triangle labeled B in Figure 50.11.

510

Meanwhile, the fall in the price received by producers leads to a fall in producer surplus. This, too, is equal to the sum of the areas of a rectangle and a triangle. The loss in producer surplus is the sum of the areas of the red rectangle labeled C and the pink triangle labeled F in Figure 50.11.

Of course, although consumers and producers are hurt by the tax, the government gains revenue. The revenue the government collects is equal to the tax per unit sold, T, multiplied by the quantity sold, Q_T. This revenue is equal to the area of a rectangle Q_T wide and T high. And we already have that rectangle in the figure: it is the sum of rectangles A and C. So the government gains part of what consumers and producers lose from an excise tax.

But a portion of the loss to producers and consumers from the tax is not offset by a gain to the government—specifically, the two triangles B and F. The deadweight loss caused by the tax is equal to the combined area of these two triangles. It represents the total surplus lost to society because of the tax—that is, the amount of surplus that would have been generated by transactions that now do not take place because of the tax.

Figure 50.12 is a version of Figure 50.11 that leaves out rectangles A (the surplus shifted from consumers to the government) and C (the surplus shifted from producers to the government) and shows only the deadweight loss, drawn here as a triangle shaded yellow. The base of that triangle is equal to the tax wedge, T; the height of the triangle is equal to the reduction in the quantity transacted due to the tax, Q_E – Q_T. Clearly, the larger the tax wedge and the larger the reduction in the quantity transacted, the greater the inefficiency from the tax. But also note an important, contrasting point: if the excise tax somehow didn’t reduce the quantity bought and sold in this market—if Q_T remained equal to Q_E after the tax was levied—the yellow triangle would disappear and the deadweight loss from the tax would be zero. So if a tax does not discourage transactions, it causes no deadweight loss. In this case, the tax simply shifts surplus straight from consumers and producers to the government.

511

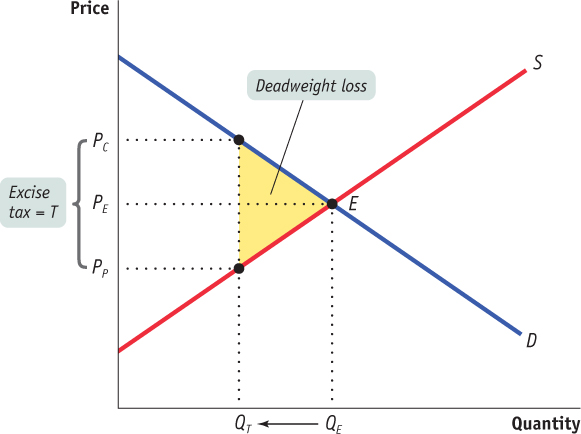
Using a triangle to measure deadweight loss is a technique used in many economic applications. For example, triangles are used to measure the deadweight loss produced by types of taxes other than excise taxes. They are also used to measure the deadweight loss produced by monopoly, another kind of market distortion. And deadweight-loss triangles are often used to evaluate the benefits and costs of public policies besides taxation—such as whether to impose stricter safety standards on a product.

In considering the total amount of inefficiency caused by a tax, we must also take into account something not shown in Figure 50.12: the resources actually used by the government to collect the tax, and by taxpayers to pay it, over and above the amount of the tax. These lost resources are called the administrative costs of the tax. The most familiar administrative cost of the U.S. tax system is the time individuals spend filling out their income tax forms or the money they spend on accountants to prepare their tax forms for them. (The latter is considered an inefficiency from the point of view of society because accountants could instead be performing other, non-tax-related services.) Included in the administrative costs that taxpayers incur are resources used to evade the tax, both legally and illegally. The costs of operating the Internal Revenue Service, the arm of the federal government tasked with collecting the federal income tax, are actually quite small in comparison to the administrative costs paid by taxpayers. The total inefficiency caused by a tax can be measured by the sum of its deadweight loss and its administrative costs.

Some extreme forms of taxation, such as the poll tax instituted by the government of British Prime Minister Margaret Thatcher in 1989, are notably unfair but very efficient. A poll tax is an example of a lump-sum tax, a tax that is the same for everyone regardless of any actions people take. The poll tax in Britain was widely perceived as much less fair than the tax structure it replaced, in which local taxes were proportional to property values.

Under the old system, the highest local taxes were paid by the people with the most expensive houses. Because these people tended to be wealthy, they were also best able to bear the burden. But the old system definitely distorted incentives to engage in mutually beneficial transactions and created deadweight loss. People who were considering home improvements knew that such improvements, by making their property more valuable, would increase their tax bills. The result, surely, was that some home improvements that would have taken place without the tax did not take place because of it. In contrast, a lump-sum tax does not distort incentives. Because under a lump-sum tax people have to pay the same amount of tax regardless of their actions, it does not cause them to substitute untaxed goods for a good whose price has been artificially inflated by a tax, as occurs with an excise tax. So lump-sum taxes, although unfair, are better than other taxes at promoting economic efficiency.

512