Tackle the Test: Free-Response Questions

1. Question

   Use the data in the table provided.

   
   

   
   

   
   

   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   

   Quantity	Total revenue	Total cost
   0	$0	$7
   1	18	23
   2	36	29
   3	54	37
   4	72	49
   5	90	65
   6	108	87
   7	126	112

   
   

   
   

   
   

   
   

   1. What is the marginal revenue of the fourth unit?

      
      
   
   

   2. Calculate profit at a quantity of two. Explain how you calculated the profit.

      
      
   
   

   3. What is the profit-maximizing level of output? Explain how to use the optimal output rule to determine the profit-maximizing level of output.

      
      
   
   

   Rubric for FRQ 1 (5 points)

   1 point: $18

   1 point: $7

   1 point: $36 - $29 or TR - TC

   1 point: 5 units

   1 point: The optimal output rule states that profit is maximized when MC = MR. Here, MC never exactly equals MR. When this occurs, the firm should produce the largest quantity at which MR exceeds MC. At a quantity of 5, MC = $16 and MR = $18. For the sixth unit, MC = $22 and MR = $18, and because MC > MR, the sixth unit would add more to total cost than it would to total revenue, and it therefore should not be produced.

2. Question

   Use a graph to illustrate the typical shape of the two curves used to find a firm’s profit-maximizing level of output on the basis of the optimal output rule. Assume all units of output can be sold for $5. Indicate the profit-maximizing level of output with a “Q*” on the appropriate axis. (You don’t have enough information to provide a specific numerical answer.) (3 points)

   Rubric for FRQ 2 (3 points)

   

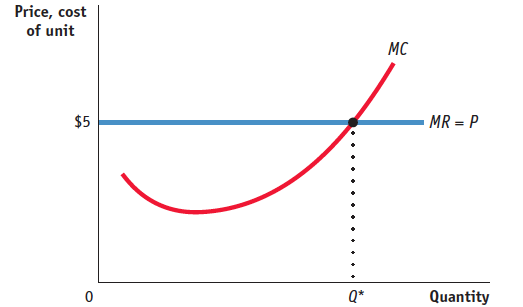
   1 point: A graph with a horizontal marginal revenue curve at a height of $5

   1 point: A marginal cost curve with a slope that starts out negative and then becomes positive as the quantity increases

   1 point: Q^* labeled on the horizontal axis below where MR = MC