The Monopolist’s Demand Curve and Marginal Revenue
Recall the firm’s optimal output rule: a profit-maximizing firm produces the quantity of output at which the marginal cost of producing the last unit of output equals marginal revenue—the change in total revenue generated by the last unit of output. That is, MR = MC at the profit-maximizing quantity of output. Although the optimal output rule holds for all firms, decisions about price and the quantity of output differ between monopolies and perfectly competitive industries due to differences in the demand curves faced by monopolists and perfectly competitive firms.
We have learned that even though the market demand curve always slopes downward, each of the firms that make up a perfectly competitive industry faces a horizontal, perfectly elastic demand curve, like DC in panel (a) of Figure 61.1. Any attempt by an individual firm in a perfectly competitive industry to charge more than the going market price will cause the firm to lose all its sales. However, it can sell as much as it likes at the market price. We saw that the marginal revenue of a perfectly competitive firm is simply the market price. As a result, the price-taking firm’s optimal output rule is to produce the output level at which the marginal cost of the last unit produced is equal to the market price.
Figure 61.1: Comparing the Demand Curves of a Perfectly Competitive Producer and a MonopolistBecause an individual perfectly competitive producer cannot affect the market price of the good, it faces a horizontal demand curve DC, as shown in panel (a). A monopolist, on the other hand, can affect the price. Because it is the sole supplier in the industry, its demand curve is the market demand curve DM , as shown in panel (b). To sell more output, it must lower the price; by reducing output, it raises the price.
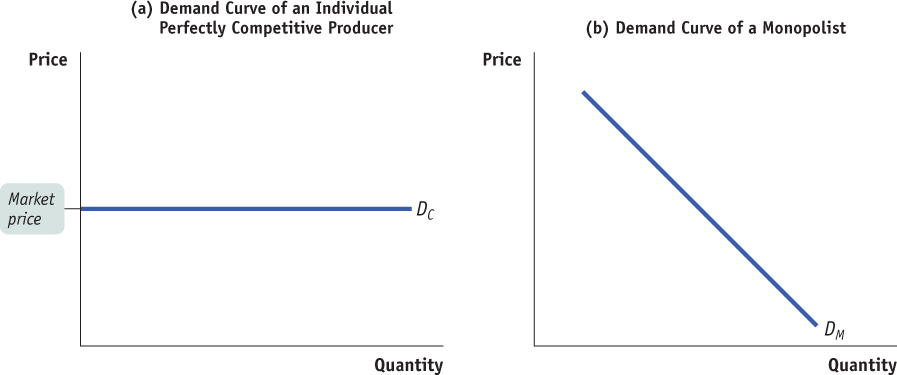
By contrast, a monopolist is the sole supplier of its good. So its demand curve is simply the market demand curve, which slopes downward, like DM in panel (b) of Figure 61.1. This downward slope creates a “wedge” between the price of the good and the marginal revenue of the good. Table 61.1 shows how this wedge develops. The first two columns of Table 61.1 show a hypothetical demand schedule for De Beers diamonds. For the sake of simplicity, we assume that all diamonds are exactly alike. And to make the arithmetic easy, we suppose that the number of diamonds sold is far smaller than is actually the case. For instance, at a price of $500 per diamond, we assume that only 10 diamonds are sold. The demand curve implied by this schedule is shown in panel (a) of Figure 61.2.
Figure 61.2: A Monopolist’s Demand, Total Revenue, and Marginal Revenue CurvesPanel (a) shows the monopolist’s demand and marginal revenue curves for diamonds from Table 61.1. The marginal revenue curve lies below the demand curve. To see why, consider point A on the demand curve, where 9 diamonds are sold at $550 each, generating total revenue of $4,950. To sell a 10th diamond, the price on all 10 diamonds must be cut to $500, as shown by point B. As a result, total revenue increases by the green area (the quantity effect: +$500) but decreases by the orange area (the price effect: −$450). So the marginal revenue from the 10th diamond is $50 (the difference between the green and orange areas), which is much lower than its price, $500. Panel (b) shows the monopolist’s total revenue curve for diamonds. As output goes from 0 to 10 diamonds, total revenue increases. It reaches its maximum at 10 diamonds—the level at which marginal revenue is equal to 0—and declines thereafter. The quantity effect dominates the price effect when total revenue is rising; the price effect dominates the quantity effect when total revenue is falling.
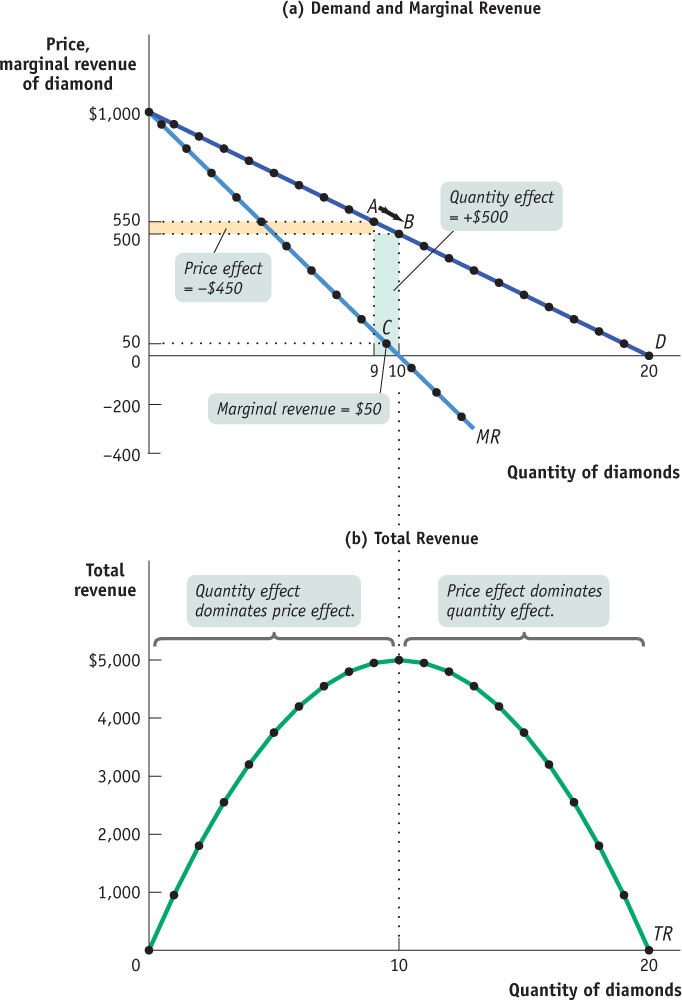
The third column of Table 61.1 shows De Beers’s total revenue from selling each quantity of diamonds—the price per diamond multiplied by the number of diamonds sold. The last column shows marginal revenue, the change in total revenue from producing and selling another diamond.
Clearly, after the 1st diamond, the marginal revenue a monopolist receives from selling one more unit is less than the price at which that unit is sold. For example, if De Beers sells 10 diamonds, the price at which the 10th diamond is sold is $500. But the marginal revenue—the change in total revenue in going from 9 to 10 diamonds—is only $50.
Why is the marginal revenue from that 10th diamond less than the price? Because an increase in production by a monopolist has two opposing effects on revenue:
A quantity effect. One more unit is sold, increasing total revenue by the price at which the unit is sold (in this case, +$500).
A price effect. In order to sell that last unit, the monopolist must cut the market price on all units sold. This decreases total revenue (in this case, by 9 × −$50 = −$450).
The quantity effect and the price effect are illustrated by the two shaded areas in panel (a) of Figure 61.2. Increasing diamond sales from 9 to 10 means moving down the demand curve from A to B, reducing the price per diamond from $550 to $500. The green-shaded area represents the quantity effect: De Beers sells the 10th diamond at a price of $500. This is offset, however, by the price effect, represented by the orange-shaded area. In order to sell that 10th diamond, De Beers must reduce the price on all its diamonds from $550 to $500. So it loses 9 × $50 = $450 in revenue, the orange-shaded area. So, as point C indicates, the total effect on revenue of selling one more diamond—the marginal revenue—derived from an increase in diamond sales from 9 to 10 is only $50.
Point C lies on the monopolist’s marginal revenue curve, labeled MR in panel (a) of Figure 61.2 and taken from the last column of Table 61.1. The crucial point about the monopolist’s marginal revenue curve is that it is always below the demand curve. That’s because of the price effect, which means that a monopolist’s marginal revenue from selling an additional unit is always less than the price the monopolist receives for that unit. It is the price effect that creates the wedge between the monopolist’s marginal revenue curve and the demand curve: in order to sell an additional diamond, De Beers must cut the market price on all units sold.
In fact, this wedge exists for any firm that possesses market power, such as an oligopolist, except in the case of price discrimination as explained in Module 63. Having market power means that the firm faces a downward-sloping demand curve. As a result, there will always be a price effect from an increase in output for a firm with market power that charges every customer the same price. So for such a firm, the marginal revenue curve always lies below the demand curve.
Corbis
Take a moment to compare the monopolist’s marginal revenue curve with the marginal revenue curve for a perfectly competitive firm, which has no market power. For such a firm there is no price effect from an increase in output: its marginal revenue curve is simply its horizontal demand curve. So for a perfectly competitive firm, market price and marginal revenue are always equal.
AP® Exam Tip
Past AP® exams have asked questions about why a monopoly's marginal revenue is below its price. Be prepared to explain that the firm must lower its price on all units sold in order to sell more units.
To emphasize how the quantity and price effects offset each other for a firm with market power, De Beers’s total revenue curve is shown in panel (b) of Figure 61.2. Notice that it is hill-shaped: as output rises from 0 to 10 diamonds, total revenue increases. This reflects the fact that at low levels of output, the quantity effect is stronger than the price effect: as the monopolist sells more, it has to lower the price on only very few units, so the price effect is small. As output rises beyond 10 diamonds, total revenue actually falls. This reflects the fact that at high levels of output, the price effect is stronger than the quantity effect: as the monopolist sells more, it now has to lower the price on many units of output, making the price effect very large. Correspondingly, the marginal revenue curve lies below zero at output levels above 10 diamonds. For example, an increase in diamond production from 11 to 12 yields only $400 for the 12th diamond, simultaneously reducing the revenue from diamonds 1 through 11 by $550. As a result, the marginal revenue of the 12th diamond is −$150.