Check Your Understanding

1. Question

   Suppose world leaders Nikita and Margaret are engaged in an arms race and face the decision of whether to build a missile. Answer the following questions using the information in the payoff matrix below, which shows how each set of actions will affect the utility of the players (the numbers represent utils gained or lost).

   

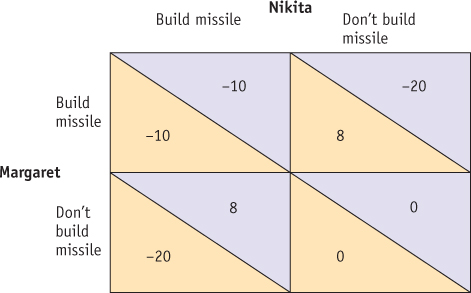
   1. Identify any Nash equilibria that exist in this game, and explain why they do or do not exist.

      A Nash equilibrium is a set of actions from which neither side wants to deviate (change actions), given what the other is doing. Both sides building a missile is a Nash equilibrium because neither player wants to deviate from the decision to build a missile. To switch from building to not building a missile, given that the other player is building a missile, would result in a change from –10 to –20 utils. There is no other Nash equilibrium in this game because for any other set of actions, at least one side is not building a missile, and would be better off switching to building a missile.

   2. Which set of actions maximizes the total payoff for Nikita and Margaret?

      The total payoff is greatest for Margaret and Nikita when neither side builds a missile, in which case their total payoff is 0 + 0 = 0.

   3. Why is it unlikely that they will choose the payoff-maximizing set of actions without some communication?

      This outcome would require cooperation because each side sees itself as better off by building a missile. If Margaret builds a missile but Nikita does not, Margaret gets a payoff of +8, rather than the 0 she obtains if she doesn’t build a missile. Similarly, Nikita is better off if he builds a missile but Margaret doesn’t: he gets a payoff of +8, rather than the 0 he obtains if he doesn’t build a missile. Indeed, both players have an incentive to build a missile regardless of what the other side does. So unless Nikita and Margaret are able to communicate in some way to enforce cooperation, they will act in their own individual interests and each will pursue its dominant strategy of building a missile.

2. Question

   Consider a new version of the game in which Richard and Justin must decide whether to go to the nightclub or the movie theater (More Games). In this version, rather than being disheartened, the two young men bond in jail and want nothing more than to be in the same place after their release. Describe any dominant strategies and Nash equilibria in this game.

   Refer students to More Games. There are no dominant strategies in this game because each player's best outcome depends on the strategy of the other player. Two Nash equilibria exist: both players going to the nightclub and both players going to the movie theater.