Tackle the Test: Free-Response Questions

1. Question

   Refer to the payoff matrix provided. You and your competitor must decide whether or not to market a new product.

   

   
   

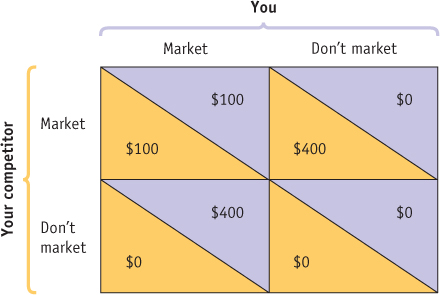
   1. If you market the new product and your competitor does not, how much profit will you earn?

      
      
   
   

   2. If you market the new product, what should your competitor do?

      
      
   
   

   3. Do you have a dominant strategy? Explain.

      
      
   
   

   4. Does this situation have a Nash equilibrium? Explain.

      
      
   
   

   Rubric for FRQ 1 (6 points)

   1 point: $400

   1 point: Market the new product

   1 point: Yes

   1 point: Profits are greater (either $100 or $400 versus $0) if I market the new product, regardless of what my competitor does.

   1 point: Yes

   1 point: Both players marketing the product is a Nash equilibrium because neither side wants to change to not marketing, given what the other side is doing. (In fact, in this case both sides want to market the product regardless of what the other side is doing, so it is a dominant strategy equilibrium as well as a Nash equilibrium.)

2. Question

   Suppose there are two firms in an oligopoly, Firm A and Firm B. If both firms charge a low price, each earns $2 million in profit. If both firms charge a high price, each earns $3 million in profit. If one firm charges a high price and one charges a low price, customers flock to the firm with the low price, and that firm earns $4 million in profit while the firm with the high price earns $1 million in profit.

   
   

   
   

   1. Draw a clearly labeled payoff matrix for this game and fill in each of the payoffs. Arrange the matrix so that Firm A is on the left, and make the upper-left set of strategies both firms choosing low prices.

      
      
   
   

   2. Identify the dominant strategy for each player, if one exists.

      
      
   
   

   3. Identify the Nash equilibria in this game, if any exist.

      
      
   
   

   4. Now suppose a tax on high-priced goods causes a $500,000 decrease in the payoffs received from charging a high price. Redraw the payoff matrix with adjustments for this change.(5 points)

      
      
   
   

   Rubric for FRQ 2 (5 points)

   

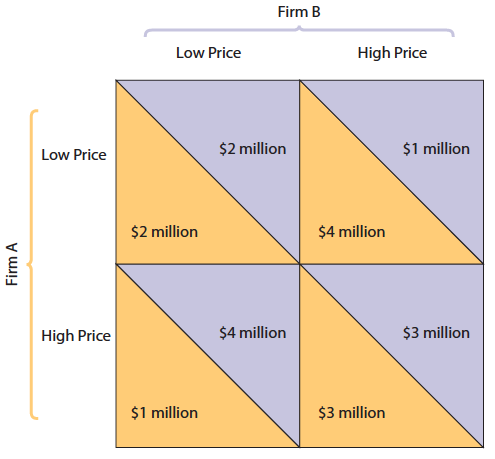
   1 point:The firm and strategy labels are correctly placed as shown above.

   1 point:The payoffs are listed correctly in the payoff matrix for part a as shown above.

   1 point:Each firm has a dominant strategy of choosing a low price.

   1 point:There is a Nash equilibrium of each firm choosing a low price.

   1 point:The payoffs are listed correctly in the payoff matrix for part d as shown below.