Indifference Curves and Consumer Choice
In the previous section we used indifference curves to represent the preferences of Ingrid, whose consumption bundles consist of rooms and restaurant meals. Our next step is to show how to use Ingrid’s indifference curve map to find her utility-
It’s important to understand how our analysis here relates to what we did in Module 51. We are not offering a new theory of consumer behavior in this module—
But as we’ll see shortly, we can derive this optimal consumer behavior in a somewhat different way—
The Marginal Rate of Substitution
The first element of our approach is a new concept, the marginal rate of substitution. We’ll see that this concept is tied closely to the shape of the indifference curve, which gets flatter moving from left to right, as illustrated in Figure D.5.
| Figure D.5 | The Changing Slope of an Indifference Curve |
We have just seen that for most goods, consumers’ indifference curves are downward-
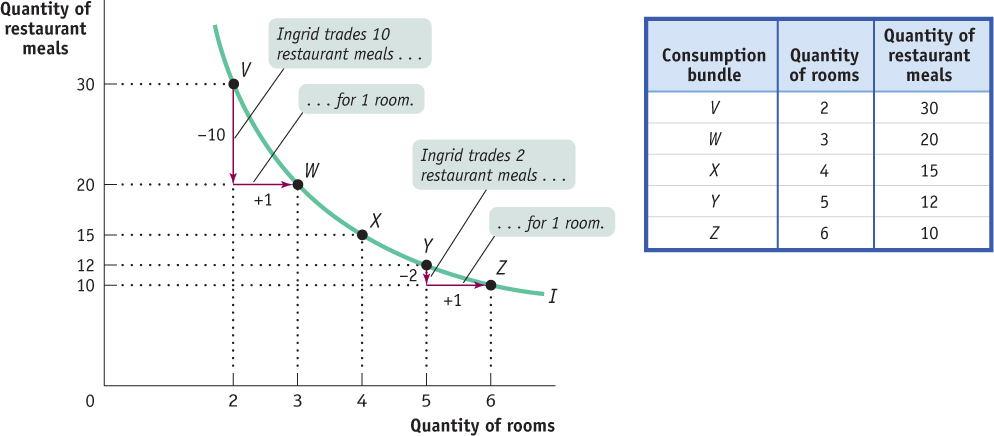
Notice that the quantity of restaurant meals that Ingrid is willing to give up in return for an additional room changes along the indifference curve. As we move from V to W, housing consumption rises from 2 to 3 rooms and restaurant meal consumption falls from 30 to 20—
To put it in terms of slope, the slope of the indifference curve between V and W is −10: the change in restaurant meal consumption, −10, divided by the change in housing consumption, 1. Similarly, the slope of the indifference curve between Y and Z is −2. So the indifference curve gets flatter as we move down it to the right—
Why does the trade-
At Y, in contrast, Ingrid consumes a much larger quantity of rooms and a much smaller quantity of restaurant meals than at V. This means that an additional room adds fewer utils, and a restaurant meal forgone costs more utils, than at V. So Ingrid is willing to give up fewer restaurant meals in return for another room of housing at Y (where she gives up 2 meals for 1 room) than she is at V (where she gives up 10 meals for 1 room).
Now let’s express the same idea—
Along the indifference curve:
(D-
or, rearranging terms,
Along the indifference curve:
(D-
Let’s now focus on what happens as we move only a short distance down the indifference curve, trading off a small increase in housing consumption in place of a small decrease in restaurant meal consumption. Following our notation from before, let’s use MUR and MUM to represent the marginal utility of rooms and restaurant meals, respectively, and ΔQR and ΔQM to represent the changes in room and meal consumption, respectively. In general, the change in total utility caused by a small change in consumption of a good is equal to the change in consumption multiplied by the marginal utility of that good. This means that we can calculate the change in Ingrid’s total utility generated by a change in her consumption bundle using the following equations:
(D-
and
(D-
So we can write Equation D-
Along the indifference curve:
(D-
Note that the left-
What we want to know is how this translates into the slope of the indifference curve. To find the slope, we divide both sides of Equation D-
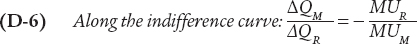
The left-
Putting all this together, Equation D-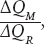 is exactly equal to the negative of the ratio of the marginal utility of a room to that of a meal, –
is exactly equal to the negative of the ratio of the marginal utility of a room to that of a meal, – 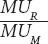 . Only when this condition is met will her total utility level remain constant as she consumes more rooms and fewer restaurant meals.
. Only when this condition is met will her total utility level remain constant as she consumes more rooms and fewer restaurant meals.
The marginal rate of substitution, or MRS, of good R in place of good M is equal to 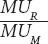 , the ratio of the marginal utility of R to the marginal utility of M.
, the ratio of the marginal utility of R to the marginal utility of M.
Economists have a special name for the ratio of the marginal utilities found in the right-
Recall that indifference curves get flatter as you move down them to the right. The reason, as we’ve just discussed, is diminishing marginal utility: as Ingrid consumes more housing and fewer restaurant meals, her marginal utility from housing falls and her marginal utility from restaurant meals rises. So her marginal rate of substitution, which is equal to the negative of the slope of her indifference curve, falls as she moves down the indifference curve.
The principle of diminishing marginal rate of substitution states that the more of one good a person consumes in proportion to a second good, the less of the second good he or she is willing to substitute for another unit of the first good.
The flattening of indifference curves as you slide down them to the right—
We can illustrate this point by referring back to Figure D.5. At point V, a bundle with a low proportion of rooms to restaurant meals, Ingrid is willing to forgo 10 restaurant meals in return for 1 room. But at point Y, a bundle with a high proportion of rooms to restaurant meals, she is willing to forgo only 2 restaurant meals in return for 1 room.
From this example we can see that, in Ingrid’s utility function, rooms and restaurant meals possess the two additional properties that characterize ordinary goods. Ingrid requires additional rooms to compensate her for the loss of a meal, and vice versa; so her indifference curves for these two goods slope downward. And her indifference curves are convex: the slope of her indifference curve—
Two goods are ordinary goods in a consumer’s utility function when (1) the consumer requires additional units of one good to compensate for fewer units of the other; and (2) the consumer experiences a diminishing marginal rate of substitution when substituting one good for the other.
With this information, we can define ordinary goods, which account for the great majority of all goods. A pair of goods are ordinary goods in a consumer’s utility function if they possess two properties: the consumer requires more of one good to compensate for less of the other, and the consumer experiences a diminishing marginal rate of substitution when substituting one good for the other.
Next we will see how to determine Ingrid’s optimal consumption bundle using indifference curves.
The Tangency Condition
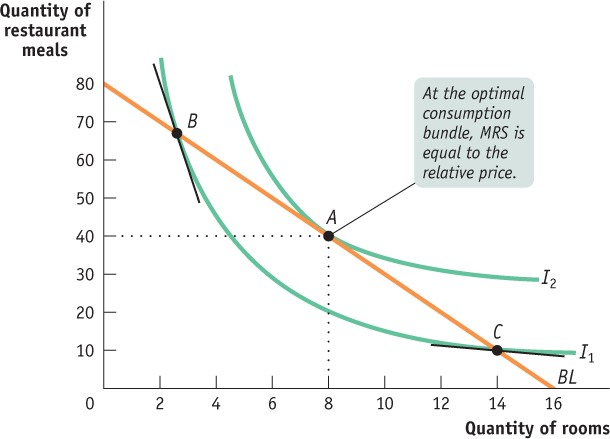
Now let’s put some of Ingrid’s indifference curves on the same diagram as her budget line to illustrate her optimal consumption choice. Figure D.6 shows Ingrid’s budget line, BL, when her income is $2,400 per month, housing costs $150 per room each month, and restaurant meals cost $30 each. What is her optimal consumption bundle?
| Figure D.6 | The Optimal Consumption Bundle |
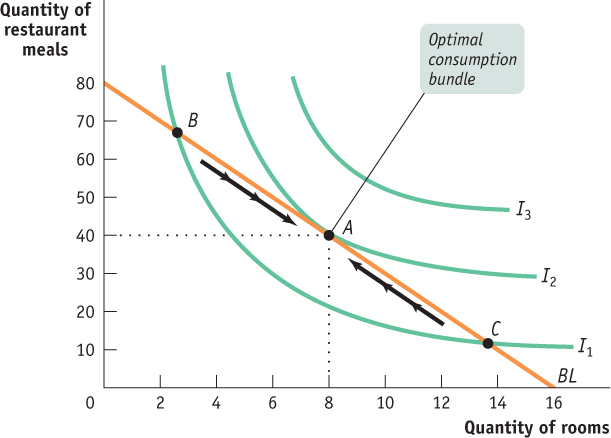
To answer this question, we consider three of Ingrid’s indifference curves: I1, I2, and I3. Of these curves, I3 represents the highest total utility level, but Ingrid cannot afford to reach that level because she is constrained by her income: no consumption bundle on her budget line yields that much total utility. But she shouldn’t settle for the total utility level generated by B, which lies on I1: there are other bundles on her budget line, such as A, that clearly yield more total utility than B.
In fact, A—a consumption bundle consisting of 8 rooms and 40 restaurant meals per month—
The tangency condition between the indifference curve and the budget line holds when the indifference curve and the budget line just touch. This condition determines the optimal consumption bundle when the indifference curves have the typical convex shape.
At the optimal consumption bundle A, Ingrid’s budget line just touches the relevant indifference curve—
To see why, let’s look more closely at how we know that a consumption bundle that doesn’t satisfy the tangency condition can’t be optimal. Reexamining Figure D.6, we can see that consumption bundles B and C are both affordable because they lie on the budget line. However, neither is optimal. Both of them lie on the indifference curve I1, which cuts through the budget line at both points. But because I1 cuts through the budget line, Ingrid can do better: she can move down the budget line from B or up the budget line from C, as indicated by the arrows. In each case, this allows her to get onto a higher indifference curve, I2, which increases her total utility.
However, Ingrid cannot do any better than I2: any other indifference curve either cuts through her budget line or doesn’t touch it at all. And the bundle that allows her to achieve I2, of course, is her optimal consumption bundle.
The Slope of the Budget Line
Figure D.6 shows us how to use a graph of the budget line and the indifference curves to find the optimal consumption bundle, the bundle at which the budget line and the indifference curve are tangent. But rather than rely on drawing graphs, we can determine the optimal consumption bundle by using a bit more math. As you can see from Figure D.6, the budget line and the indifference curve have the same slope at the optimal consumption bundle, A. Why? Because two curves can only be tangent to each other if they have the same slope at the point where they meet. Otherwise, they would cross each other at that point. And we know that if we are on an indifference curve that crosses the budget line (like I1, in Figure D.6), we can’t be on the indifference curve that contains the optimal consumption bundle (like I2).
So we can use information about the slopes of the budget line and the indifference curve to find the optimal consumption bundle. To do that, we must first analyze the slope of the budget line, a fairly straightforward task. We know that Ingrid will get the highest possible utility by spending all of her income and consuming a bundle on her budget line. So we can represent Ingrid’s budget line, made up of the consumption bundles available to her when she spends all of her income, with the equation:
(D-
where N stands for Ingrid’s income. To find the slope of the budget line, we divide its vertical intercept (where the budget line hits the vertical axis) by its horizontal intercept (where it hits the horizontal axis) and then add a negative sign. The vertical intercept is the point at which Ingrid spends all her income on restaurant meals and none on housing (that is, QR = 0). In that case the number of restaurant meals she consumes is:

At the other extreme, Ingrid spends all her income on housing and none on restaurant meals (so that QM = 0). This means that at the horizontal intercept of the budget line, the number of rooms she consumes is:
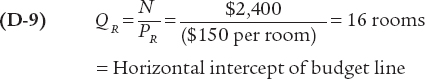
Now we have the information needed to find the slope of the budget line. It is:
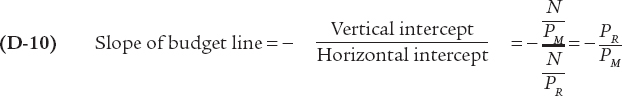
The relative price of good R in terms of good M is equal to 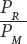 , the rate at which R trades for M in the market.
, the rate at which R trades for M in the market.
Notice the negative sign in Equation D-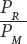 is known as the relative price of rooms in terms of restaurant meals, to distinguish it from an ordinary price in terms of dollars. Because buying one more room requires Ingrid to give up the quantity
is known as the relative price of rooms in terms of restaurant meals, to distinguish it from an ordinary price in terms of dollars. Because buying one more room requires Ingrid to give up the quantity 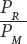 of restaurant meals, or 5 meals, we can interpret the relative price
of restaurant meals, or 5 meals, we can interpret the relative price 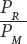 as the rate at which a room trades for restaurant meals in the market; it is the price—
as the rate at which a room trades for restaurant meals in the market; it is the price—
Looking at this another way, the slope of the budget line—
In contrast, a change in the relative price 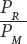 will lead to a change in the slope of the budget line. We’ll analyze these changes in the budget line and how the optimal consumption bundle changes when the relative price changes or when income changes in greater detail later in the module.
will lead to a change in the slope of the budget line. We’ll analyze these changes in the budget line and how the optimal consumption bundle changes when the relative price changes or when income changes in greater detail later in the module.
Prices and the Marginal Rate of Substitution
Now we’re ready to bring together the slope of the budget line and the slope of the indifference curve to find the optimal consumption bundle. From Equation D-
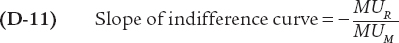
The relative price rule says that at the optimal consumption bundle, the marginal rate of substitution between two goods is equal to their relative price.
As we’ve already noted, at the optimal consumption bundle the slope of the budget line and the slope of the indifference curve are equal. We can write this formally by putting Equations D-

That is, at the optimal consumption bundle, the marginal rate of substitution between any two goods is equal to the ratio of their prices. To put it in a more intuitive way, starting with Ingrid’s optimal consumption bundle, the rate at which she would trade a room for more restaurant meals along her indifference curve, 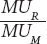 , is equal to the rate at which rooms are traded for restaurant meals in the market,
, is equal to the rate at which rooms are traded for restaurant meals in the market, 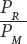 .
.
What would happen if this equality did not hold? We can see by examining
Figure D.7. There, at point B, the slope of the indifference curve, –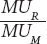 , is greater in absolute value than the slope of the budget line, –
, is greater in absolute value than the slope of the budget line, –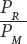 . This means that, at B, Ingrid values an additional room in place of meals more than it costs her to buy an additional room and forgo some meals. As a result, Ingrid would be better off moving down her budget line toward A, consuming more rooms and fewer restaurant meals—
. This means that, at B, Ingrid values an additional room in place of meals more than it costs her to buy an additional room and forgo some meals. As a result, Ingrid would be better off moving down her budget line toward A, consuming more rooms and fewer restaurant meals—
| Figure D.7 | Understanding the Relative Price Rule |
But suppose we transform the last term of Equation D-

So using either the optimal consumption rule or the relative price rule, we find the same optimal consumption bundle.
Preferences and Choices
Now that we have seen how to represent the optimal consumption choice in an indifference curve diagram, we can turn briefly to the relationship between consumer preferences and consumer choices.
When we say that two consumers have different preferences, we mean that they have different utility functions. This in turn means that they will have indifference curve maps with different shapes. And those different maps will translate into different consumption choices, even among consumers with the same income and who face the same prices.
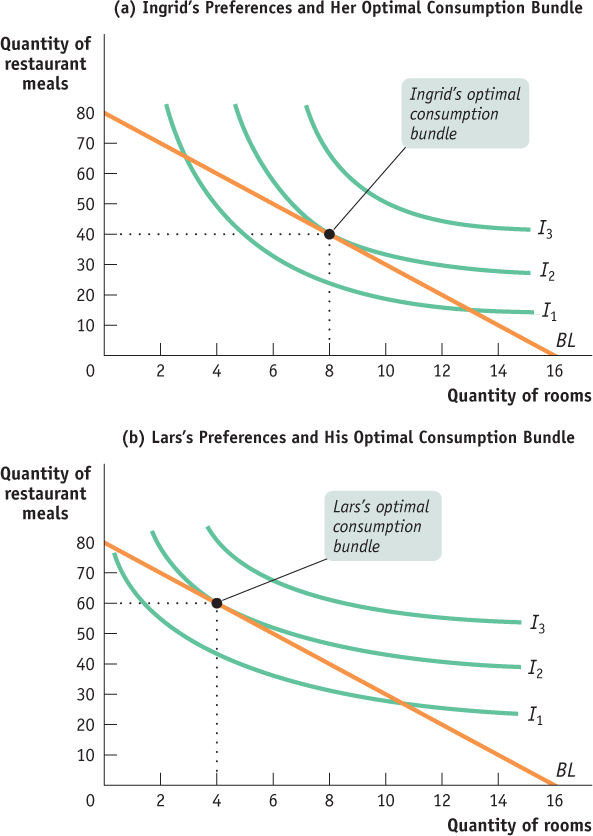
To see this, suppose that Ingrid’s friend Lars also consumes only housing and restaurant meals. However, Lars has a stronger preference for restaurant meals and a weaker preference for housing. This difference in preferences is shown in Figure D.8, which shows two sets of indifference curves: panel (a) shows Ingrid’s preferences and panel (b) shows Lars’s preferences. Note the difference in their shapes.
Suppose, as before, that rooms cost $150 per month and restaurant meals cost $30. Let’s also assume that both Ingrid and Lars have incomes of $2,400 per month, giving them identical budget lines. Nonetheless, because they have different preferences, they will make different consumption choices, as shown in Figure D.8. Ingrid will choose 8 rooms and 40 restaurant meals, whereas Lars will choose 4 rooms and 60 restaurant meals.
| Figure D.8 | Differences in Preferences |