Free-Response Review Questions
Question
Each of the combinations of song and movie downloads shown in the table below give Kathleen an equal level of utility.
Quantity of songs Quantity of movies 0 8 1 6 2 4 3 2 4 0 Graph Kathleen’s indifference curve.
Economists believe that each individual indifference curve for ordinary goods exhibits what two properties?
Does Kathleen’s indifference curve exhibit the two properties from part b? Explain.
Each of the combinations of song and movie downloads shown in the table below give Kathleen an equal level of utility.Rubric for FRQ 1 (8 points)
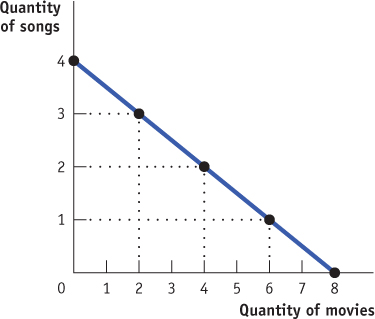
1 point: Axes labeled “Quantity of songs” and “Quantity of movies”
1 point: Correctly plotted indifference curve points
1 point: Negative slope
1 point: Convex shape
1 point: Negative slope—
yes 1 point: As more movies are downloaded, there must be fewer song downloads to give Kathleen the same level of utility as before. This trade-
off of more of one good for less of another gives the indifference curve a negative slope. 1 point: Convex shape—
no 1 point: The indifference curve is a straight line with a constant slope, rather than being a convex line with a slope that decreases in absolute value from left to right.
Question
Kathleen has $20 to spend on song and movie downloads each week. The price of a song download is $2 and the price of a movie download is $5.
Graph Kathleen’s budget line.
Suppose all of Kathleen’s indifference curves have the same shape and slope as the one in Question 1. How many song and movie downloads will Kathleen purchase to maximize her utility? Explain.
(4 points)
Kathleen has $20 to spend on song and movie downloads each week. The price of a song download is $2 and the price of a movie download is $5.
Discussion Starters
Question
What would it indicate about your preferences for two items if your indifference curves were vertical? Can you think of examples of pairs of items for which this is the case?
This would indicate that you didn’t care at all about the good on the vertical axis, because as you get more of that good, you remain on the same indifference curve. Getting more of the good on the horizontal axis puts you on a different vertical indifference curve so that good would matter to you. For example, if the number of golf balls on the moon were measured on the vertical axis and the number of pairs of sunglasses you own were measured on the horizontal axis, you might have vertical indifference curves.Question
Suppose that on a Saturday afternoon you must divide your time between studying and playing sports, and both activities are free. Could you use a budget constraint and indifference curves to model this decision? Explain your answer.
Yes, a budget constraint for time could be used to model this situation. The budget constraint would start at a point that represents spending all afternoon studying and end at a point that represents spending all afternoon playing sports. The indifference curves would have their usual shape.Question
Consider the dilemma of how much money to spend now and how much to set aside for the future. Is this another trade-
off that could be modeled with a budget constraint and indifference curves? What makes it possible to spend more now than you actually have? If you spend less than you have now, what can you do with your money so that the amount you have to spend in the future grows? What rate associated with these opportunities affects the slope of the budget constraint? Yes, this could be modeled with a budget constraint and indifference curves as well. Borrowing makes it possible to spend more now than you actually have. If you spend less than you have now, you can lend your money and have more to spend in the future when the loan is repaid. The interest rate at which money is borrowed and lent would affect the slope of the budget constraint.