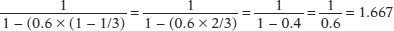In contrast to autonomous taxation, with endogenous taxation the government captures some of the increase in real GDP. Specifically, let’s assume that the government “captures” a fraction, t, of any increase in real GDP in the form of taxes, where t, the tax rate, is a fraction between 0 and 1. And let’s repeat the exercise we carried out in Chapter 11, where we consider the effects of a $100 billion increase in investment spending. The same analysis holds for any autonomous increase in aggregate expenditure—in particular, it is also true for increases in government purchases of goods and services.

The $100 billion increase in investment spending initially raises real GDP by $100 billion (the first round). In the absence of taxes, disposable income would rise by $100 billion. But because part of the rise in real GDP is collected in the form of taxes, disposable income only rises by (1 − t) × $100 billion. The second-round increase in consumer spending, which is equal to the marginal propensity to consume (MPC) multiplied by the rise in disposable income, is (MPC × (1 − t)) × $100 billion. This leads to a third-round increase in consumer spending of (MPC × (1 − t)) × (MPC × (1 − t)) × $100 billion, and so on. So the total effect on real GDP is:

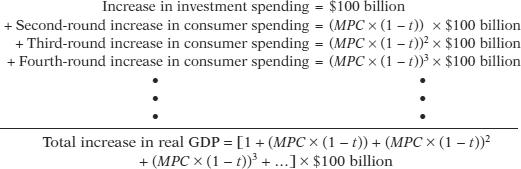
As we pointed out in Chapter 11, an infinite series of the form 1 + x + x² + …, with 0 < x < 1, is equal to 1/(1 − x). In this example, x = (MPC × (1 − t)). So the total effect of a $100 billion increase in investment spending, taking into account all the subsequent increases in consumer spending, is to raise real GDP by:

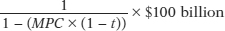
The government captures a fraction of any increase in real GDP, in the form of taxes. That is, if t is the tax rate, then T = t × GDP. Also, as stated above,

Again, since disposable income, YD, is GDP after subtracting taxes and adding transfers, then:

The income–expenditure equilibrium level of GDP, Y*, is equal to planned aggregate expenditure:

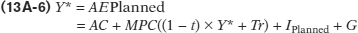
Again, with some manipulation, we get:

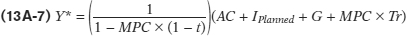
This equation gives us the following two multipliers:

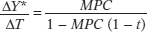
There is no autonomous taxation multiplier here since taxes now depend on income only. When we calculated the multiplier assuming away the effect of taxes, we found that it was 1/(1 − MPC). But when we assume that a fraction, t, of any change in real GDP is collected in the form of taxes, the multiplier is:

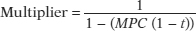
This is always a smaller number than 1/(1 − MPC), and its size diminishes as t grows. Suppose, for example, that MPC = 0.6. In the absence of taxes, this implies a multiplier of 1/(1 − 0.6) = 1/0.4 = 2.5. But now let’s assume that t = 1/3, that is, that 1/3 of any increase in real GDP is collected by the government. Then the multiplier is: