In 2011 and 2012, Americans were facing sticker shock at the gas pump: the price of a gallon of regular gasoline had risen from an average of $1.61 at the end of December 2008 to close to $4. Many other prices were also up. Some prices, though, were heading down: electronics and some foods, like eggs, were coming down from a run-up in late 2010. Yet practically everyone felt that the overall cost of living was rising. But how fast?

Clearly, there was a need for a single number summarizing what was happening to consumer prices. Just as macroeconomists find it useful to have a single number representing the overall level of output, they also find it useful to have a single number representing the overall level of prices: the aggregate price level. Yet a huge variety of goods and services are produced and consumed in the economy. How can we summarize the prices of all these goods and services with a single number? The answer lies in the concept of a price index, which we’ll introduce with an example.

Suppose that a frost in Florida destroys most of the citrus harvest. As a result, the price of an orange rises from $0.20 to $0.40, the price of a grapefruit rises from $0.60 to $1.00, and the price of a lemon rises from $0.25 to $0.45. How much has the price of citrus fruit increased?

One way to answer that question is to state three numbers—the changes in prices for oranges, grapefruit, and lemons. But this is a very cumbersome method. Rather than having to recite three numbers in an effort to track changes in the prices of citrus fruit, we would prefer to have some kind of overall measure of the average price change.

To measure average price changes for consumer goods and services, economists track changes in the cost of a typical consumer’s consumption bundle—the typical basket of goods and services purchased before the price changes. A hypothetical consumption bundle, used to measure changes in the overall price level, is known as a market basket. Suppose that before the frost a typical consumer bought 200 oranges, 50 grapefruit, and 100 lemons over the course of a year, our market basket for this example.

Table 13-3 shows the pre-frost and post-frost cost of this market basket. Before the frost, it cost $95; after the frost, the same bundle of goods cost $175. Since $175/$95 = 1.842, the post-frost basket costs 1.842 times the cost of the pre-frost basket, a cost increase of 84.2%. In this example, the average price of citrus fruit has increased 84.2% since the base year as a result of the frost, where the base year is the initial year used in the measurement of the price change.

369

Economists use the same method to measure changes in the overall price level: they track changes in the cost of buying a given market basket. In addition, they perform another simplification in order to avoid having to keep track of the information that the market basket cost—for example, to avoid saying that the market basket costs $95 in 1997 dollars and $103 in 2001 dollars. They normalize the measure of the aggregate price level, which means that they set the cost of the market basket equal to 100 in the chosen base year. Working with a market basket and a base year, and after performing normalization, we obtain what is known as a price index, a normalized measure of the overall price level. It is always cited along with the year for which the aggregate price level is being measured and the base year. A price index can be calculated using the following formula:

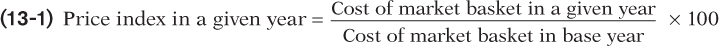
In our example, the citrus fruit market basket cost $95 in the base year, the year before the frost. So by Equation 13-1 we define the price index for citrus fruit as (cost of market basket in a given year/$95) × 100, yielding an index of 100 for the period before the frost and 184.2 after the frost. You should note that the price index for the base year always results in a price index equal to 100. This is because the price index in the base year is equal to: (cost of market basket in base year/cost of market basket in base year) × 100 = 100.

Thus, the price index makes it clear that the average price of citrus has risen 84.2% as a consequence of the frost. Because of its simplicity and intuitive appeal, the method we’ve just described is used to calculate a variety of price indexes to track average price changes among a variety of different groups of goods and services. For example, the consumer price index, which we’ll discuss shortly, is the most widely used measure of the aggregate price level, the overall price level of final consumer goods and services across the economy.

Price indexes are also the basis for measuring inflation. The inflation rate is the annual percent change in an official price index. The inflation rate from year 1 to year 2 is calculated using the following formula, where we assume that year 1 and year 2 are consecutive years.

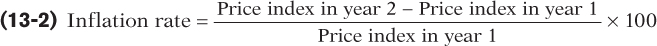
Typically, a news report that cites “the inflation rate” is referring to the annual percent change in the consumer price index.

The most widely used measure of prices in the United States is the consumer price index (often referred to simply as the CPI), which is intended to show how the cost of all purchases by a typical urban family has changed over time. It is calculated by surveying market prices for a market basket that is constructed to represent the consumption of a typical family of four living in a typical American city. The base period for the index is currently 1982–1984; that is, the index is calculated so that the average of consumer prices in 1982–1984 is 100.

370

The market basket used to calculate the CPI is far more complex than the three-fruit market basket we described above. In fact, to calculate the CPI, the Bureau of Labor Statistics sends its employees out to survey supermarkets, gas stations, hardware stores, and so on—some 23,000 retail outlets in 87 cities. Every month it tabulates about 80,000 prices, on everything from romaine lettuce to a medical check-up.

Figure 13-3 shows the weight of major categories in the consumer price index as of December 2014. For example, motor fuel, mainly gasoline, accounted for 4% of the CPI in December 2014. So when gas prices fell nearly 50%, from $3.71 a gallon in the summer of 2014 to $2.04 a gallon in early 2015, the effect was to decrease the CPI by 0.5 times 4%—that is, around 2%.

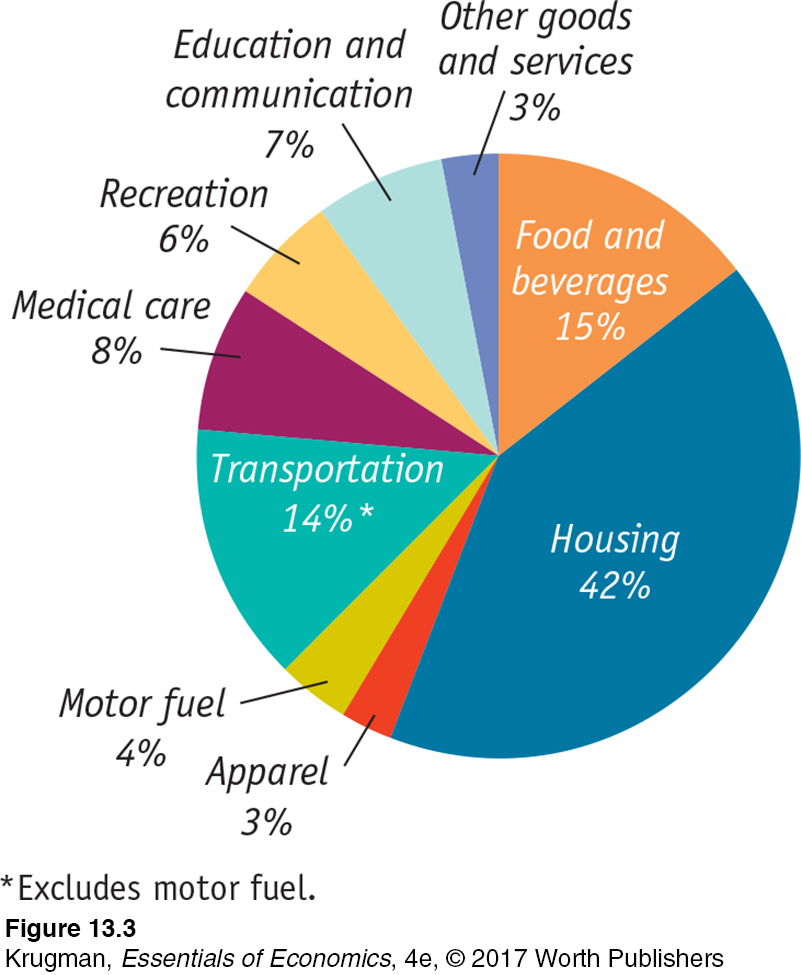
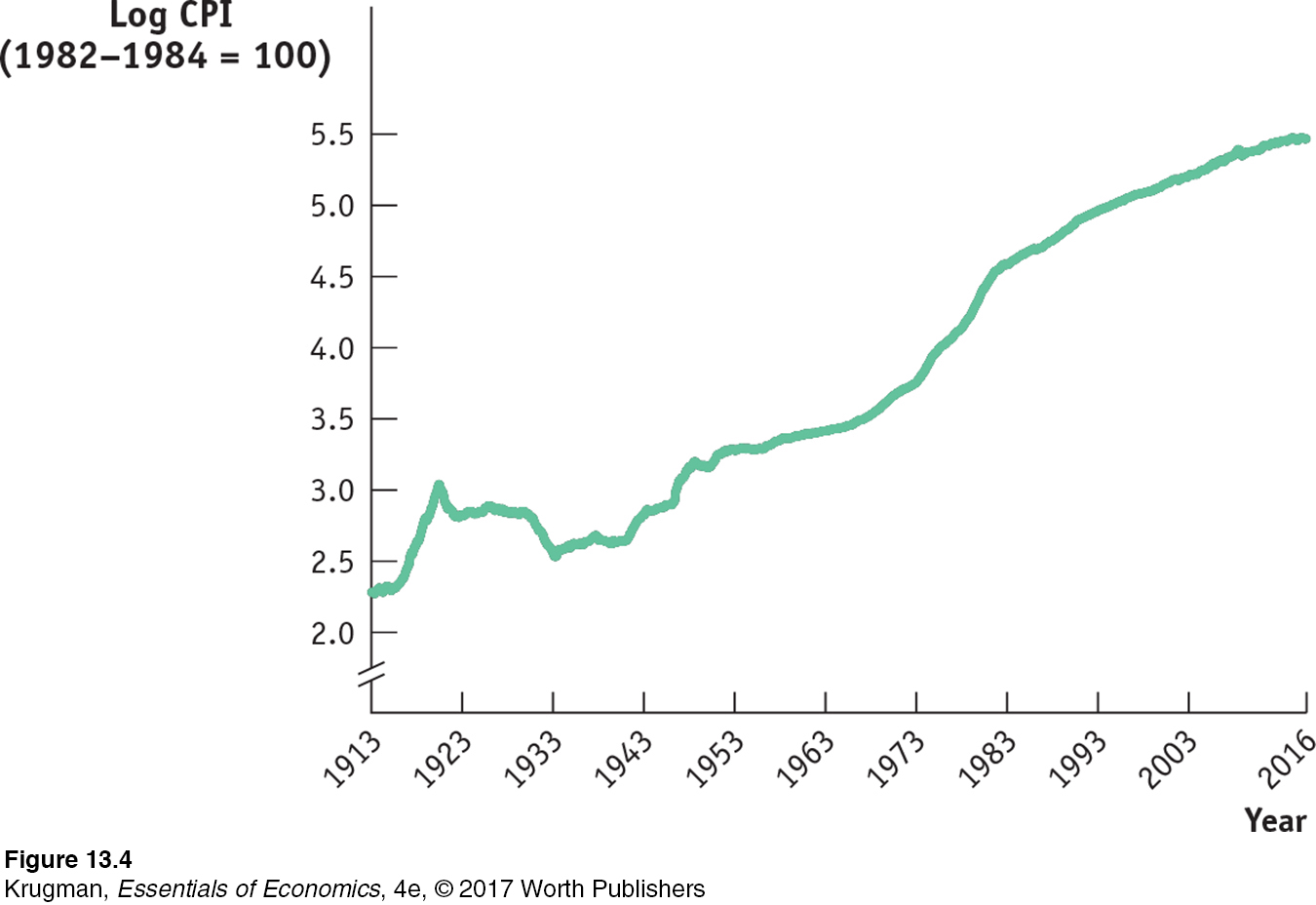
Figure 13-4 shows how the CPI has changed since measurement began in 1913. Since 1940, the CPI has risen steadily, although its annual percent increases in recent years have been much smaller than those of the 1970s and early 1980s. (A logarithmic scale is used so that equal percent changes in the CPI have the same slope.)

The United States, like nearly every country, calculates a consumer price index. As you might expect, the market baskets that make up these indexes differ quite a lot from country to country. In poor countries, where people must spend a high proportion of their income to feed themselves, food makes up a large share of the price index. Among high-income countries, differences in consumption patterns lead to differences in the price indexes: the Japanese price index puts a larger weight on raw fish and a smaller weight on beef than ours does, and the French price index puts a larger weight on wine.

371

There are two other price measures that are also widely used to track economy-wide price changes. One is the producer price index (or PPI, which used to be known as the wholesale price index). As its name suggests, the producer price index measures the cost of a typical basket of goods and services—containing raw commodities such as steel, electricity, coal, and so on—purchased by producers. Because commodity producers are relatively quick to change prices when they perceive a change in overall demand for their goods, the PPI often responds to inflationary or deflationary pressures more quickly than the CPI. As a result, the PPI is often regarded as an “early warning signal” of changes in the inflation rate.

The other widely used price measure is the GDP deflator; it isn’t exactly a price index, although it serves the same purpose. Recall how we distinguished between nominal GDP (GDP in current prices) and real GDP (GDP calculated using the prices of a base year). The GDP deflator for a given year is equal to 100 times the ratio of nominal GDP for that year to real GDP for that year. Since real GDP is currently expressed in 2005 dollars, the GDP deflator for 2005 is equal to 100. If nominal GDP doubles but real GDP does not change, the GDP deflator indicates that the aggregate price level doubled.

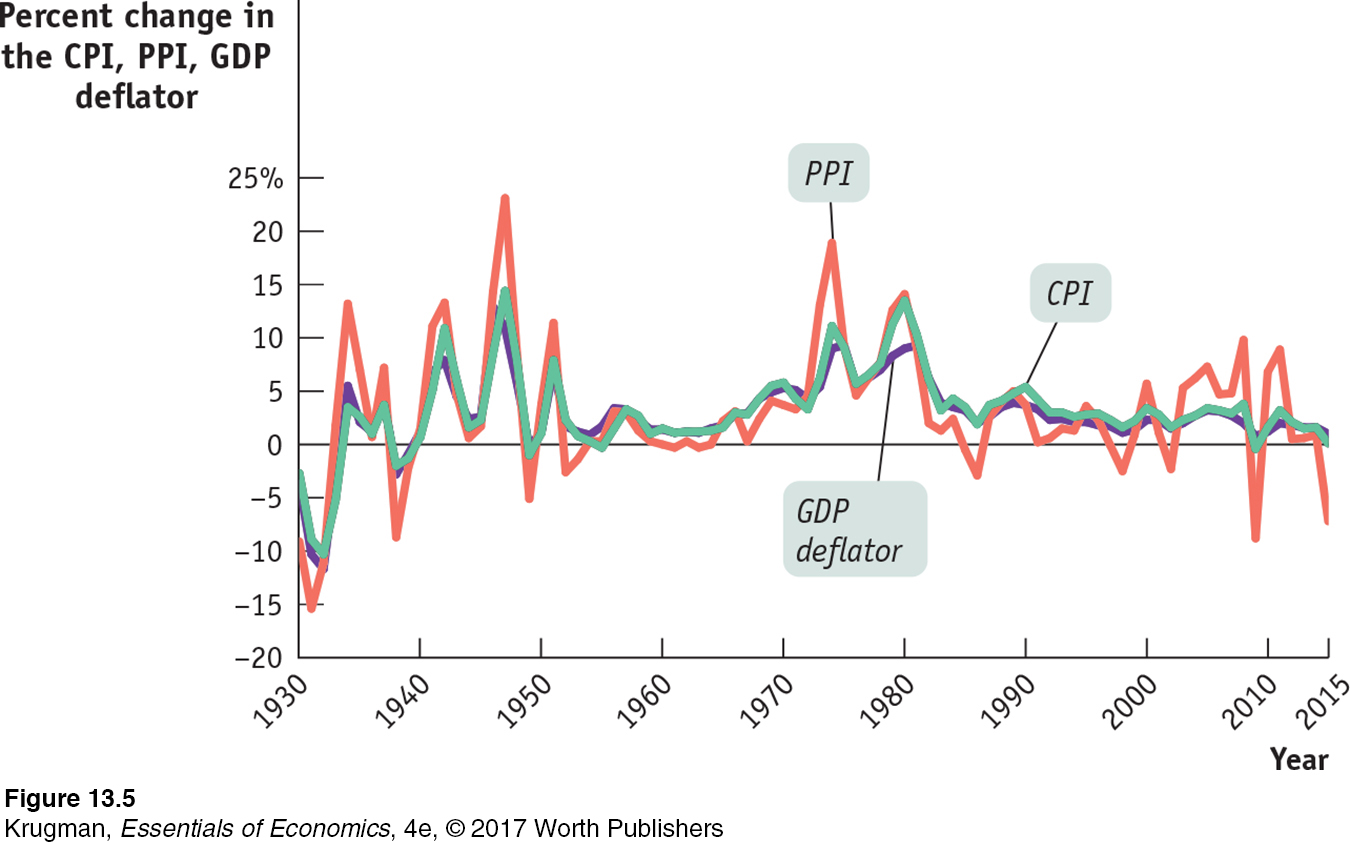
Perhaps the most important point about the different inflation rates generated by these three measures of prices is that they usually move closely together (although the producer price index tends to fluctuate more than either of the other two measures). Figure 13-5 shows the annual percent changes in the three indexes since 1930. By all three measures, the U.S. economy experienced deflation during the early years of the Great Depression, inflation during World War II, accelerating inflation during the 1970s, and a return to relative price stability in the 1990s. Notice, by the way, the dramatic ups and downs in producer prices from 2000 to 2015 on the graph; this reflects large swings in energy and food prices, which play a much bigger role in the PPI than they do in either the CPI or the GDP deflator.

372