In Chapters 7 and 10 we learned that a buyer of a bond is entitled to receive a fixed sum of interest each year over the life of the bond and, at the end, a repayment of principal (the face value of the bond: the amount lent when the bond was issued). Let’s illustrate how we can use present value to price a bond with a simple example.

Suppose you are offered the chance to purchase a bond issued by Facebook. It was issued two years ago to mature in seven years’ time. That is, it pays interest for seven years total, at the end of which the principal is repaid. As of today, then, the bond will pay interest for five more years. Assume that the principal on this Facebook bond is $1,000. Also assume that when it was issued it paid an interest rate of 6%, equal to the current market equilibrium interest rate. So the amount of interest that the owner of this bond receives every year is $1,000 × 0.6 = $60. This annual interest payment is known generally as the coupon.

To answer this question we need to calculate the present value of the future interest payments from this bond based on today’s market equilibrium interest rate. Suppose that the market equilibrium interest rate has dropped from 6% when the bond was issued two years ago to 5% today. Then the present value of this bond is equal to the present value of the annual $60 coupon for the remaining five years plus the present value of the repayment of the $1,000 principal at the end of the five years:

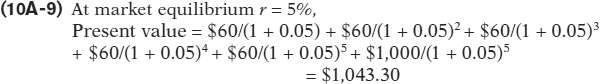
(Your calculated value may be slightly different due to rounding error.)

This means you should be willing to pay no more than $1,043.30 for this Facebook bond. At a higher price you would be better off spending your $1,043.30 on a newly issued bond that pays an interest rate of 5% for the next five years. This example illustrates a general rule: when determining the price of a preexisting bond, the interest rate used to calculate that price is the current market equilibrium interest rate (5% in this example), not the interest rate that was current when the bond was originally issued (6% in this example).

To gain further understanding, let’s calculate what the present value of that same bond would be today if the equilibrium interest rate had not fallen and had instead remained at 6%:

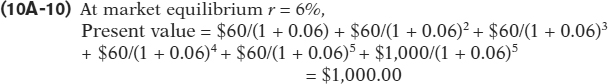
(Again, your calculated value may be slightly different due to rounding error.)

Equation 10A-10 illustrates a general principle: when the current market equilibrium interest rate is unchanged from when the bond was issued, then the present value of the bond is equal to its face value, regardless of how many periods are left until it matures. You can check this for yourself by recalculating the present value for the bond when r = 6% and four years are left to maturity. Your answer should be approximately $1,000.00.

By comparing Equations 10A-9 and 10A-10, you can see that the price of the bond goes up when the market equilibrium interest rate falls. Conversely, the price of a bond falls when the market equilibrium interest rate goes up.

In the real world there is an additional complicating factor when pricing a bond: risk. Some bonds are riskier than others because the bond issuer is perceived to be less likely to repay bondholders in full. A high-risk bond will sell at a lower price than a low-risk bond with the same maturity, face value, and annual coupon payments. That lower price compensates the owner of the high-risk bond for the risk she faces of not being repaid in full.

Ignoring the problem of risk, the general formula for bond pricing is as follows, where n is the number of years to maturity, C is the annual coupon, F is the face value, and i is the current market equilibrium interest rate on comparable bonds:

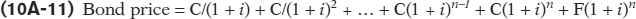
We can conclude that when the market interest rate on comparable bonds rises, the price of existing bonds falls; when the market interest rate on comparable bonds falls, the price of existing bonds rises.

While a bond entitles its owner to interest payments, a share of stock entitles its owner to a share of the company’s profits. That’s because a share of stock represents ownership of a portion of the company. As we explained in Chapter 7, a share of a company’s profits paid to a shareholder is called a dividend. So a share entitles its owner to a series of payments of future dividends, and we can use the present value formula to find the price of a share of stock:

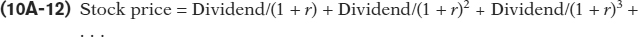
In the formula, r is the interest rate in the market for loanable funds. Unlike the formula for a bond price in Equation 10A-11, there is no end date, n, in the formula for a stock because a share entitles its owner to dividend payments indefinitely.

It’s possible to simplify Equation 10A-12 if we assume that the company’s profits grow at a constant rate every year, and its dividends grow at a constant rate. Then the stock price formula becomes:

Like bond pricing, stock pricing comes with real-world complicating factors for investors to consider: First, dividends paid by most businesses are highly variable (much more than bond payments) because profits vary from year to year. So stock prices are based upon expected future dividend payments. Second, the stock market is affected by rumors, fads, and other types of irrational behavior, so stock prices fluctuate far more than bond prices.