Spending the Marginal Dollar
As we’ve just seen, we can find Sammy’s optimal consumption choice by finding the total utility he receives from each consumption bundle on his budget line and then choosing the bundle at which total utility is maximized. But we can use marginal analysis instead, turning Sammy’s problem of finding his optimal consumption choice into a “how much” problem.
How do we do this? By thinking about choosing an optimal consumption bundle as a problem of how much to spend on each good. That is, to find the optimal consumption bundle with marginal analysis, we ask whether Sammy can make himself better off by spending a little bit more of his income on clams and less on potatoes, or by doing the opposite—
The marginal utility per dollar spent on a good or service is the additional utility from spending one more dollar on that good or service.
Our first step in applying marginal analysis is to ask if Sammy is made better off by spending an additional dollar on either good; and if so, by how much is he better off. To answer this question we must calculate the marginal utility per dollar spent on either clams or potatoes—
Marginal Utility per Dollar
We’ve already introduced the concept of marginal utility, the additional utility a consumer gets from consuming one more unit of a good or service; now let’s see how this concept can be used to derive the related measure of marginal utility per dollar.
Table 10-3 shows how to calculate the marginal utility per dollar spent on clams and potatoes, respectively.
10-3
Sammy’s Marginal Utility per Dollar
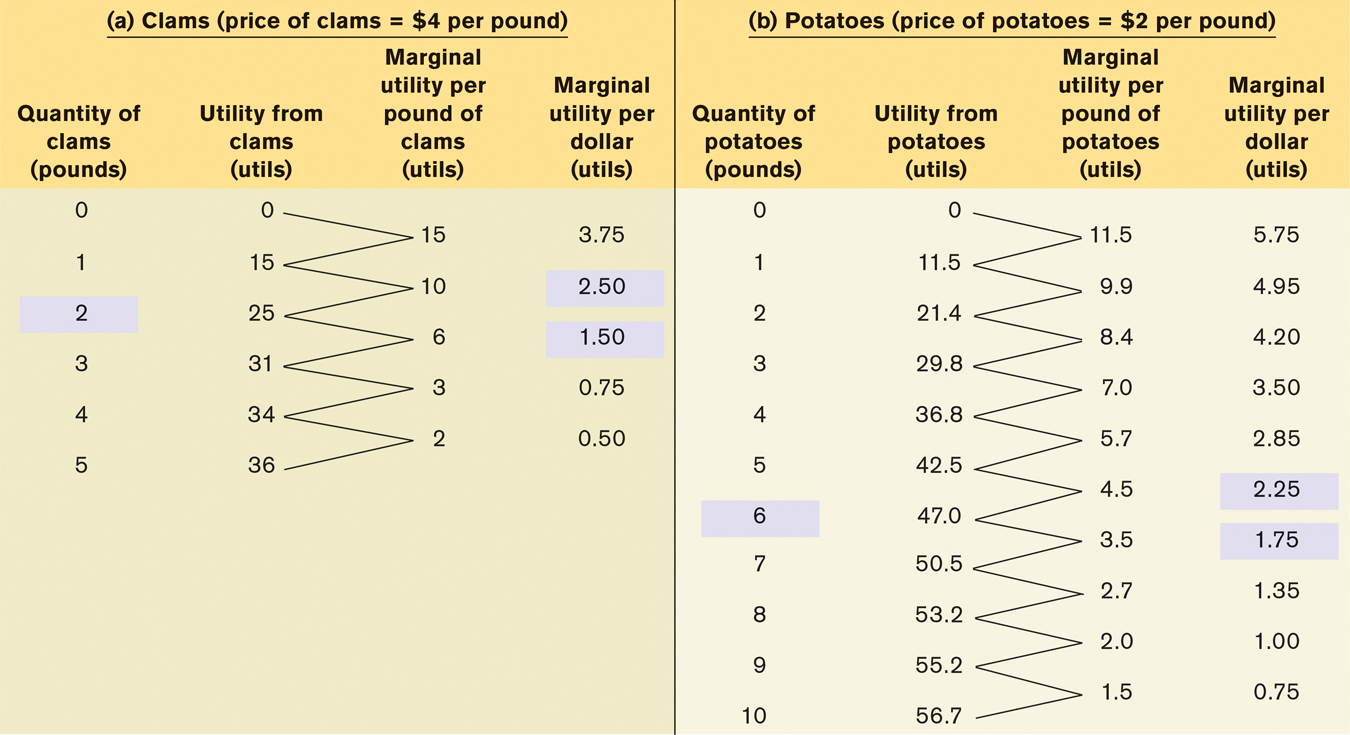
In panel (a) of the table, the first column shows different possible amounts of clam consumption. The second column shows the utility Sammy derives from each amount of clam consumption; the third column then shows the marginal utility, the increase in utility Sammy gets from consuming an additional pound of clams. Panel (b) provides the same information for potatoes. The next step is to derive marginal utility per dollar for each good. To do this, we must divide the marginal utility of the good by its price in dollars.
To see why we must divide by the price, compare the third and fourth columns of panel (a). Consider what happens if Sammy increases his clam consumption from 2 pounds to 3 pounds. As we can see, this increase in clam consumption raises his total utility by 6 utils. But he must spend $4 for that additional pound, so the increase in his utility per additional dollar spent on clams is 6 utils/$4 = 1.5 utils per dollar.
Similarly, if he increases his clam consumption from 3 pounds to 4 pounds, his marginal utility is 3 utils but his marginal utility per dollar is 3 utils/$4 = 0.75 util per dollar. Notice that because of diminishing marginal utility, Sammy’s marginal utility per pound of clams falls as the quantity of clams he consumes rises. As a result, his marginal utility per dollar spent on clams also falls as the quantity of clams he consumes rises.
So the last column of panel (a) shows how Sammy’s marginal utility per dollar spent on clams depends on the quantity of clams he consumes. Similarly, the last column of panel (b) shows how his marginal utility per dollar spent on potatoes depends on the quantity of potatoes he consumes. Again, marginal utility per dollar spent on each good declines as the quantity of that good consumed rises, because of diminishing marginal utility.
We will use the symbols MUC and MUP to represent the marginal utility per pound of clams and potatoes, respectively. And we will use the symbols PC and PP to represent the price of clams (per pound) and the price of potatoes (per pound). Then the marginal utility per dollar spent on clams is MUC/PC and the marginal utility per dollar spent on potatoes is MUP/PP. In general, the additional utility generated from an additional dollar spent on a good is equal to:
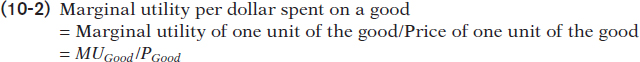
Now let’s see how this concept helps us derive a consumer’s optimal consumption using marginal analysis.
Optimal Consumption
Let’s consider Figure 10-4. As in Figure 10-3, we can measure both the quantity of clams and the quantity of potatoes on the horizontal axis due to the budget constraint. Along the horizontal axis of Figure 10-4—also as in Figure 10-3—the quantity of clams increases as you move from left to right, and the quantity of potatoes increases as you move from right to left. The curve labeled MUC/PC in Figure 10-4 shows Sammy’s marginal utility per dollar spent on clams as derived in Table 10-3. Likewise, the curve labeled MUP/PP shows his marginal utility per dollar spent on potatoes. Notice that the two curves, MUC/PC and MUP/PP, cross at the optimal consumption bundle, point C, consisting of 2 pounds of clams and 6 pounds of potatoes.
10-4
Marginal Utility per Dollar
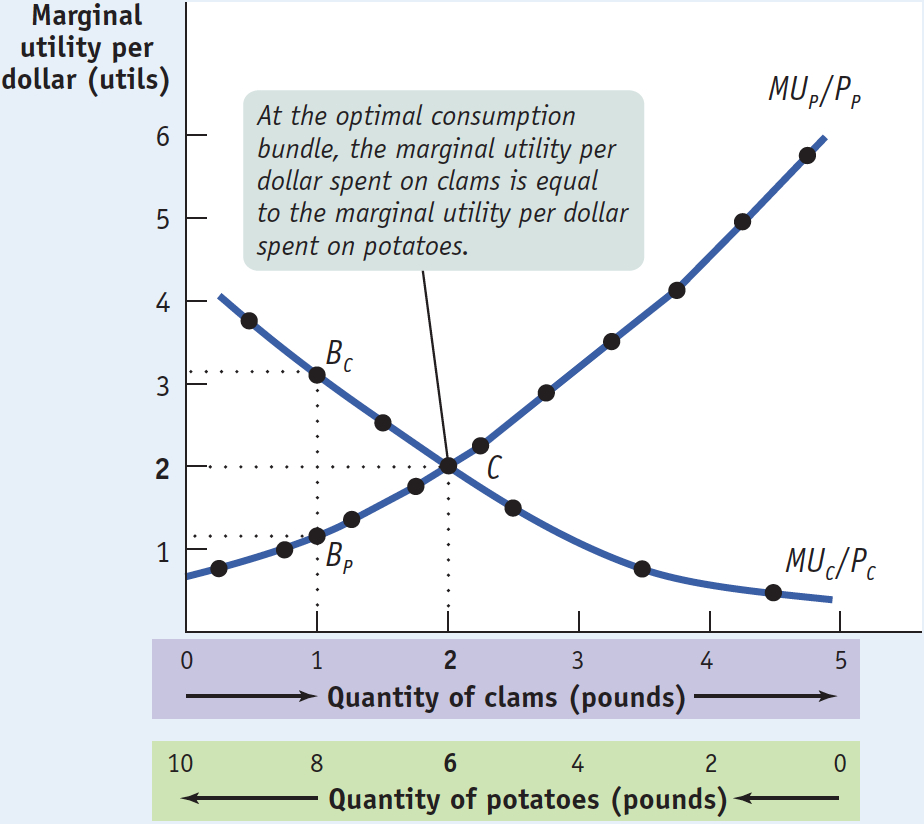
Moreover, Figure 10-4 illustrates an important feature of Sammy’s optimal consumption bundle: when Sammy consumes 2 pounds of clams and 6 pounds of potatoes, his marginal utility per dollar spent is the same, 2, for both goods. That is, at the optimal consumption bundle MUC/PC = MUP/PP = 2.
PITFALLS: THE RIGHT MARGINAL COMPARISON
THE RIGHT MARGINAL COMPARISON
Marginal analysis solves “how much” decisions by weighing costs and benefits at the margin: the benefit of doing a little bit more versus the cost of doing a little bit more. However, as we noted in Chapter 9, the form of the marginal analysis can differ, depending upon whether you are making a production decision that maximizes profits or a consumption decision that maximizes utility. Let’s review that difference again to make sure that it’s clearly understood.
In Chapter 9, Alex’s decision was a production decision because the problem he faced was maximizing the profit from years of schooling. The optimal quantity of years that maximized his profit was found using marginal analysis: at the optimal quantity, the marginal benefit of another year of schooling was equal to its marginal cost. Alex did not face a budget constraint because he could always borrow to finance another year of school.
But if you were to extend the way we solved Alex’s production problem to Sammy’s consumption problem without any change in form, you might be tempted to say that Sammy’s optimal consumption bundle is the one at which the marginal utility of clams is equal to the marginal utility of potatoes, or that the marginal utility of clams was equal to the price of clams. But both those statements would be wrong because they don’t properly account for the budget constraint and the fact that consuming more of one good requires consuming less of another.
In a consumption decision, your objective is to maximize the utility that your limited budget can deliver. And the right way to find the optimal consumption bundle is to set the marginal utility per dollar equal for each good in the consumption bundle. When this condition is satisfied, the “bang per buck” is the same across all the goods and services you consume. Only then is there no way to rearrange your consumption and get more utility from your budget.
This isn’t an accident. Consider another one of Sammy’s possible consumption bundles—
How do we know this? If Sammy’s marginal utility per dollar spent on clams is higher than his marginal utility per dollar spent on potatoes, he has a simple way to make himself better off while staying within his budget: spend $1 less on potatoes and $1 more on clams. We can illustrate this with points BC and BP in Figure 10-4. By spending an additional dollar on clams, he gains the amount of utility given by BC, about 3 utils. By spending $1 less on potatoes, he loses the amount of utility given by BP, only about 1 util.
Because his marginal utility per dollar spent is higher for clams than for potatoes, reallocating his spending toward clams and away from potatoes would increase his total utility. But if his marginal utility per dollar spent on potatoes is higher, he can increase his utility by spending less on clams and more on potatoes. So if Sammy has in fact chosen his optimal consumption bundle, his marginal utility per dollar spent on clams and potatoes must be equal.
According to the utility-
This is a general principle, which we call the utility-
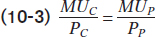
It’s easiest to understand this rule using examples in which the consumption bundle contains only two goods, but it applies no matter how many goods or services a consumer buys: in the optimal consumption bundle, the marginal utilities per dollar spent for each and every good or service in that bundle are equal.
ECONOMICS in Action: Buying Your Way Out of Temptation
Buying Your Way Out of Temptation

It might seem odd to pay more to get less. But snack food I companies have discovered that consumers are indeed willing to pay more for smaller portions, and exploiting this trend is a recipe for success. A company executive explained why small packages are popular—
It’s clear that in this case consumers are making a calculation: the extra utility gained from not having to worry about whether they’ve eaten too much is worth the extra cost. As one shopper said, “They’re pretty expensive, but they’re worth it. It’s individually packaged for the amount I need, so I don’t go overboard.” So it’s clear that consumers aren’t being irrational here. Rather, they’re being entirely rational: in addition to their snack, they’re buying a little hand-
Quick Review
According to the utility-
maximizing principle of marginal analysis , the marginal utility per dollar—the marginal utility of a good divided by its price—is the same for all goods in the optimal consumption bundle. Whenever marginal utility per dollar is higher for one good than for another good, the consumer should spend $1 more on the good with the higher marginal utility per dollar and $1 less on the other. By doing this the consumer will move closer to his or her optimal consumption bundle.
10-3
Question 10.5
In Table 10-3 you can see that marginal utility per dollar spent on clams and marginal utility per dollar spent on potatoes are equal when Sammy increases his consumption of clams from 3 pounds to 4 pounds and his consumption of potatoes from 9 pounds to 10 pounds. Explain why this is not Sammy’s optimal consumption bundle. Illustrate your answer using the budget line in Figure 10-3.
From Table 10-3 you can see that Sammy’s marginal utility per dollar from increasing his consumption of clams from 3 pounds to 4 pounds and his marginal utility per dollar from increasing his consumption of potatoes from 9 to 10 pounds are the same, 0.75 utils. But a consumption bundle consisting of 4 pounds of clams and 10 pounds of potatoes is not Sammy’s optimal consumption bundle because it is not affordable given his income of $20; 4 pounds of clams and 10 pounds of potatoes costs $4 × 4 + $2 × 10 = $36, $16 more than Sammy’s income. This can be illustrated with Sammy’s budget line from panel (a) of Figure 10-3: a bundle of 4 pounds of clams and 10 pounds of potatoes is represented by point X in the accompanying diagram, a point that lies outside Sammy’s budget line. If you look at the horizontal axis of panel (a) of Figure 10-3, it is quite clear that there is no such thing in Sammy’s consumption possibilities as a bundle consisting of 4 pounds of clams and 10 pounds of potatoes.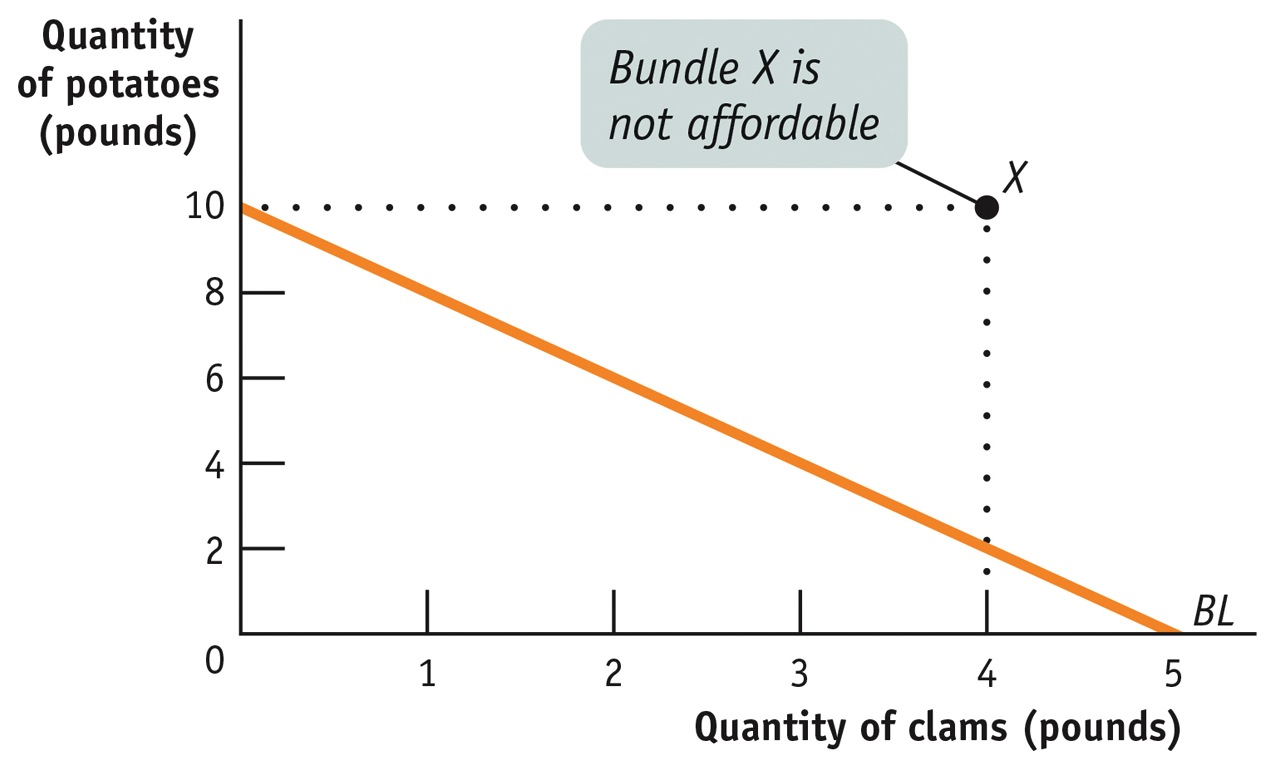
Question 10.6
Explain what is faulty about the following statement, using data from Table 10-3: “In order to maximize utility, Sammy should consume the bundle that gives him the maximum marginal utility per dollar for each good.
Sammy’s maximum utility per dollar is generated when he goes from consuming 0 to 1 pound of clams (3.75 utils) and as he goes from 0 to 1 pound of potatoes (5.75 utils). But this bundle consisting of 1 pound of clams and 1 pound of potatoes generates only 26.5 utils for him. Instead, Sammy should choose the consumption bundle that satisfies his budget constraint and for which the marginal utility per dollar for both goods is equal.
Solutions appear at back of book.