Now that we’ve seen how to analyze consumer choice using indifference curves, we can get some payoffs from our new technique. First up is a new insight into the distinction between substitutes and complements.

Back in Chapter 3, we pointed out that the price of one good often affects the demand for another but that the direction of this effect can go either way: a rise in the price of tea increases the demand for coffee, but a rise in the price of cream reduces the demand for coffee. Tea and coffee are substitutes; cream and coffee are complements.

But what determines whether two goods are substitutes or complements? It depends on the shape of a consumer’s indifference curves. This relationship can be illustrated with two extreme cases: the cases of perfect substitutes and perfect complements.

Consider Cokie, who likes cookies. She isn’t particular: it doesn’t matter to her whether she has 3 peanut butter cookies and 7 chocolate chip cookies, or vice versa. What would her indifference curves between peanut butter and chocolate chip cookies look like?

The answer is that they would be straight lines like I₁ and I₂ in Figure 10A-9. For example, I₁ shows that any combination of peanut butter cookies and chocolate chip cookies that adds up to 10 cookies yields Cokie the same utility.

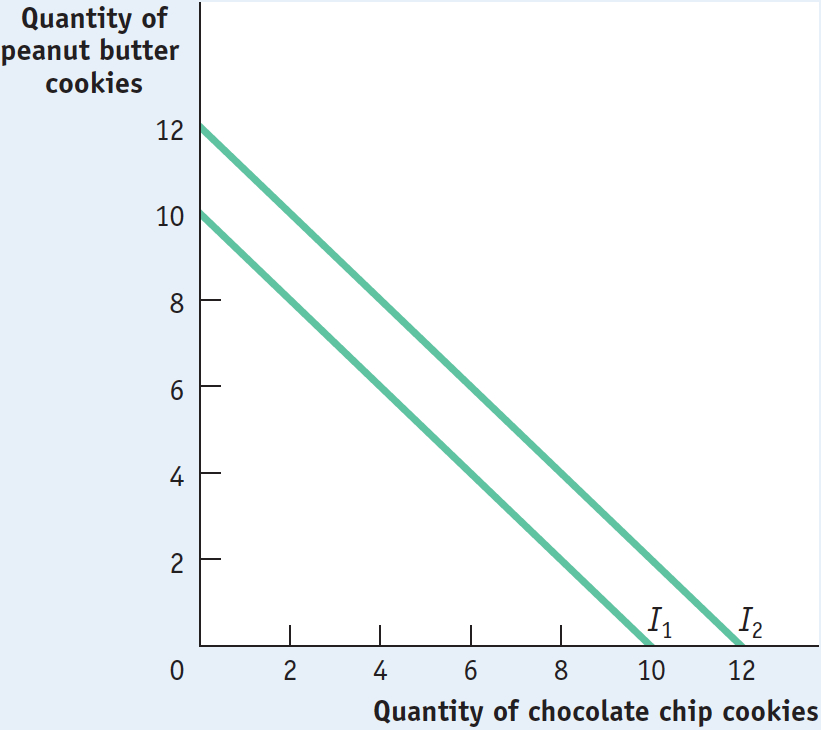
A consumer whose indifference curves are straight lines is always willing to substitute the same amount of one good in place of one unit of the other, regardless of how much of either good he or she consumes. Cokie, for example, is always willing to accept one less peanut butter cookie in exchange for one more chocolate chip cookie, making her marginal rate of substitution constant.

When indifference curves are straight lines, we say that goods are perfect substitutes. When two goods are perfect substitutes, there is only one relative price at which consumers will be willing to purchase both goods; a slightly higher or lower relative price will cause consumers to buy only one of the two goods.

Figure 10A-10 illustrates this point. The indifference curves are the same as those in Figure 10A-9, but now we include Cokie’s budget line, BL. In each panel we assume that Cokie has $12 to spend. In panel (a) we assume that chocolate chip cookies cost $1.20 and peanut butter cookies cost $1.00. Cokie’s optimal consumption bundle is then at point A: she buys 12 peanut butter cookies and no chocolate chip cookies. In panel (b) the situation is reversed: chocolate chip cookies cost $1.00 and peanut butter cookies cost $1.20. In this case, her optimal consumption is at point B, where she consumes only chocolate chip cookies.

Why does such a small change in the price cause Cokie to switch all her consumption from one good to the other? Because her marginal rate of substitution is constant and therefore doesn’t depend on the composition of her consumption bundle. If the relative price of chocolate chip cookies is more than the marginal rate of substitution of chocolate chip cookies in place of peanut butter cookies, she buys only peanut butter cookies; if it is less, she buys only chocolate chip. And if the relative price of chocolate chip cookies is equal to the marginal rate of substitution, Cokie can maximize her utility by buying any bundle on her budget line. That is, she will be equally happy with any combination of chocolate chip cookies and peanut butter cookies that she can afford. As a result, in this case we cannot predict which particular bundle she will choose among all the bundles that lie on her budget line.

The case of perfect substitutes represents one extreme form of consumer preferences; the case of perfect complements represents the other. Goods are perfect complements when a consumer wants to consume two goods in the same ratio, regardless of their relative price.

Suppose that Aaron likes cookies and milk—but only together. An extra cookie without an extra glass of milk yields no additional utility; neither does an extra glass of milk without another cookie. In this case, his indifference curves will form right angles, as shown in Figure 10A-11.

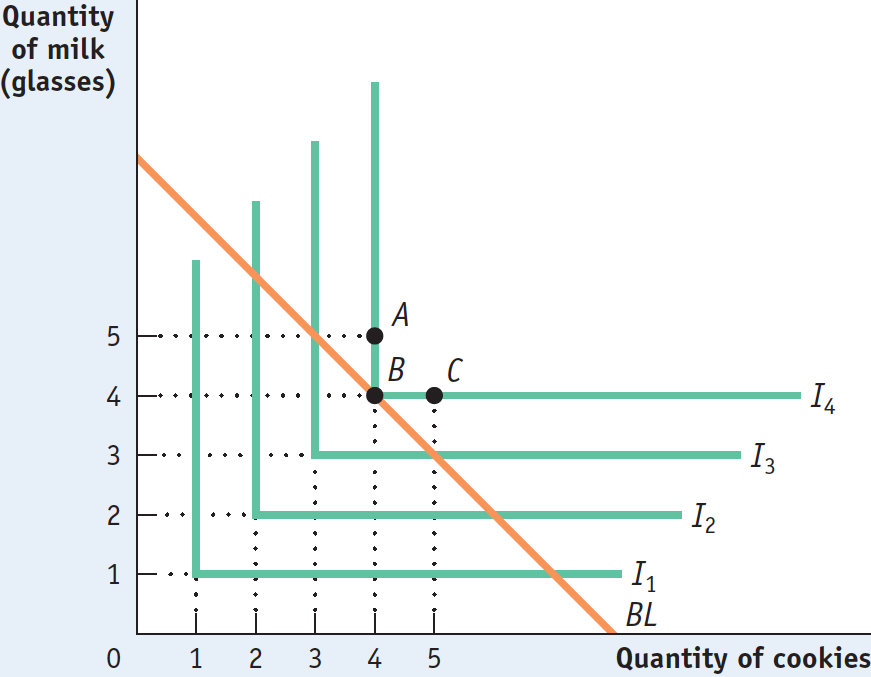
To see why, consider the three bundles labeled A, B, and C. At B, on I₄, Aaron consumes 4 cookies and 4 glasses of milk. At A, he consumes 4 cookies and 5 glasses of milk; but the extra glass of milk adds nothing to his utility. So A is on the same indifference curve as B, I₄. Similarly, at C he consumes 5 cookies and 4 glasses of milk, but this yields the same total utility as 4 cookies and 4 glasses of milk. So C is also on the same indifference curve, I₄.

Also shown in Figure 10A-11 is a budget line that would allow Aaron to choose bundle B. The important point is that the slope of the budget line has no effect on his relative consumption of cookies and milk. This means that he will always consume the two goods in the same proportions regardless of prices—which makes the goods perfect complements.

You may be wondering what happened to the marginal rate of substitution in Figure 10A-11. That is, exactly what is Aaron’s marginal rate of substitution between cookies and milk, given that he is unwilling to make any substitutions between them? The answer is that in the case of perfect complements, the marginal rate of substitution is undefined because an individual’s preferences don’t allow any substitution between goods.

There are real-world examples of pairs of goods that are very close to being perfect substitutes. For example, the list of ingredients on a package of Bisquick pancake mix says that it contains “soybean and/or cottonseed oil”: the producer uses whichever is cheaper, since consumers can’t tell the difference. There are other pairs of goods that are very close to being perfect complements—for example, cars and tires.

In most cases, however, the possibilities for substitution lie somewhere between these extremes. In some cases it isn’t easy to be sure whether goods are substitutes or complements.