Marginal Productivity and Factor Demand
All economic decisions are about comparing costs and benefits—
Although there are some important exceptions, most factor markets in the modern American economy are perfectly competitive, meaning that buyers and sellers of a given factor are price-
Value of the Marginal Product
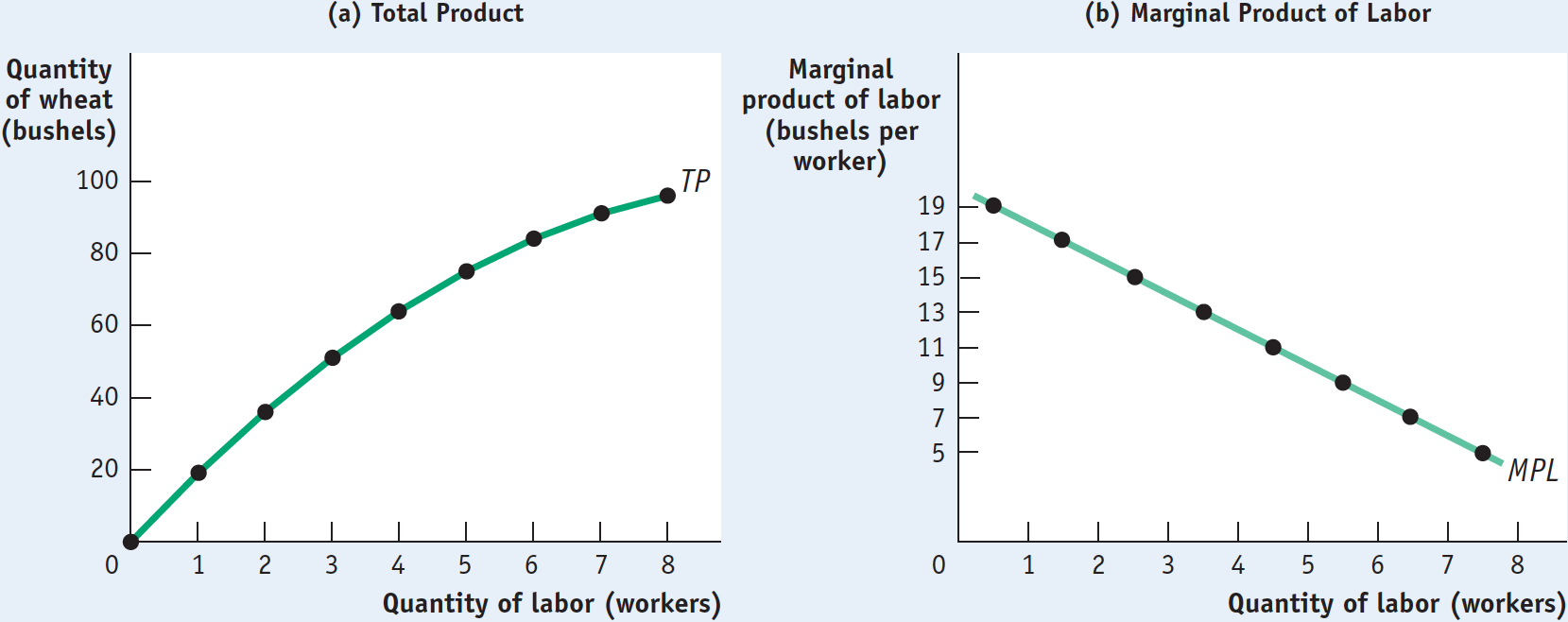
Figure 19-2 reproduces Figures 11-1 and 11-2, which showed the production function for wheat on George and Martha’s farm. Panel (a) uses the total product curve to show how total wheat production depends on the number of workers employed on the farm; panel (b) shows how the marginal product of labor, the increase in output from employing one more worker, depends on the number of workers employed. Table 19-1, which reproduces the table in Figure 11-1, shows the numbers behind the figure.
19-2
The Production Function and Marginal Product of Labor Curve for George and Martha’s Farm
19-1
Employment and Output for George and Martha’s Farm

Assume that George and Martha want to maximize their profit, that workers must be paid $200 each, and that wheat sells for $20 per bushel. What is their optimal number of workers? That is, how many workers should they employ to maximize profit?
In Chapters 11 and 12 we showed how to answer this question in several steps. In Chapter 11 we used information from the producer’s production function to derive the firm’s total cost and its marginal cost. And in Chapter 12 we derived the price-
There is, however, another way to use marginal analysis to find the number of workers that maximizes a producer’s profit. We can go directly to the question of what level of employment maximizes profit. This alternative approach is equivalent to the approach we outlined in the preceding paragraph—
The value of the marginal product of a factor is the value of the additional output generated by employing one more unit of that factor.
To see how this alternative approach works, let’s suppose that George and Martha are considering whether or not to employ an additional worker. The increase in cost from employing that additional worker is the wage rate, W. The benefit to George and Martha from employing that extra worker is the value of the extra output that worker can produce. What is this value? It is the marginal product of labor, MPL, multiplied by the price per unit of output, P. This amount—
(19-
So should George and Martha hire that extra worker? The answer is yes if the value of the extra output is more than the cost of the worker—
So the decision to hire labor is a marginal decision, in which the marginal benefit to the producer from hiring an additional worker (VMPL) should be compared with the marginal cost to the producer (W). And as with any marginal decision, the optimal choice is where marginal benefit is just equal to marginal cost. That is, to maximize profit George and Martha will employ workers up to the point at which, for the last worker employed:
(19-
This rule doesn’t apply only to labor; it applies to any factor of production. The value of the marginal product of any factor is its marginal product times the price of the good it produces. The general rule is that a profit-
It’s important to realize that this rule doesn’t conflict with our analysis in Chapters 11 and 12. There we saw that a profit-
Now let’s look more closely at why choosing the level of employment at which the value of the marginal product of the last worker employed is equal to the wage rate works—
Value of the Marginal Product and Factor Demand
19-2
Value of the Marginal Product of Labor for George and Martha’s Farm

The value of the marginal product curve of a factor shows how the value of the marginal product of that factor depends on the quantity of the factor employed.
Table 19-2 calculates the value of the marginal product of labor on George and Martha’s farm, on the assumption that the price of wheat is $20 per bushel. In Figure 19-3 the horizontal axis shows the number of workers employed; the vertical axis measures the value of the marginal product of labor and the wage rate. The curve shown is the value of the marginal product curve of labor. This curve, like the marginal product of labor curve, slopes downward because of diminishing returns to labor in production. That is, the value of the marginal product of each worker is less than that of the preceding worker, because the marginal product of each worker is less than that of the preceding worker.
We have just seen that to maximize profit, George and Martha must hire workers up to the point at which the wage rate is equal to the value of the marginal product of the last worker employed. Let’s use the example to see how this principle really works.
Assume that George and Martha currently employ 3 workers and that workers must be paid the market wage rate of $200. Should they employ an additional worker?
19-3
The Value of the Marginal Product Curve
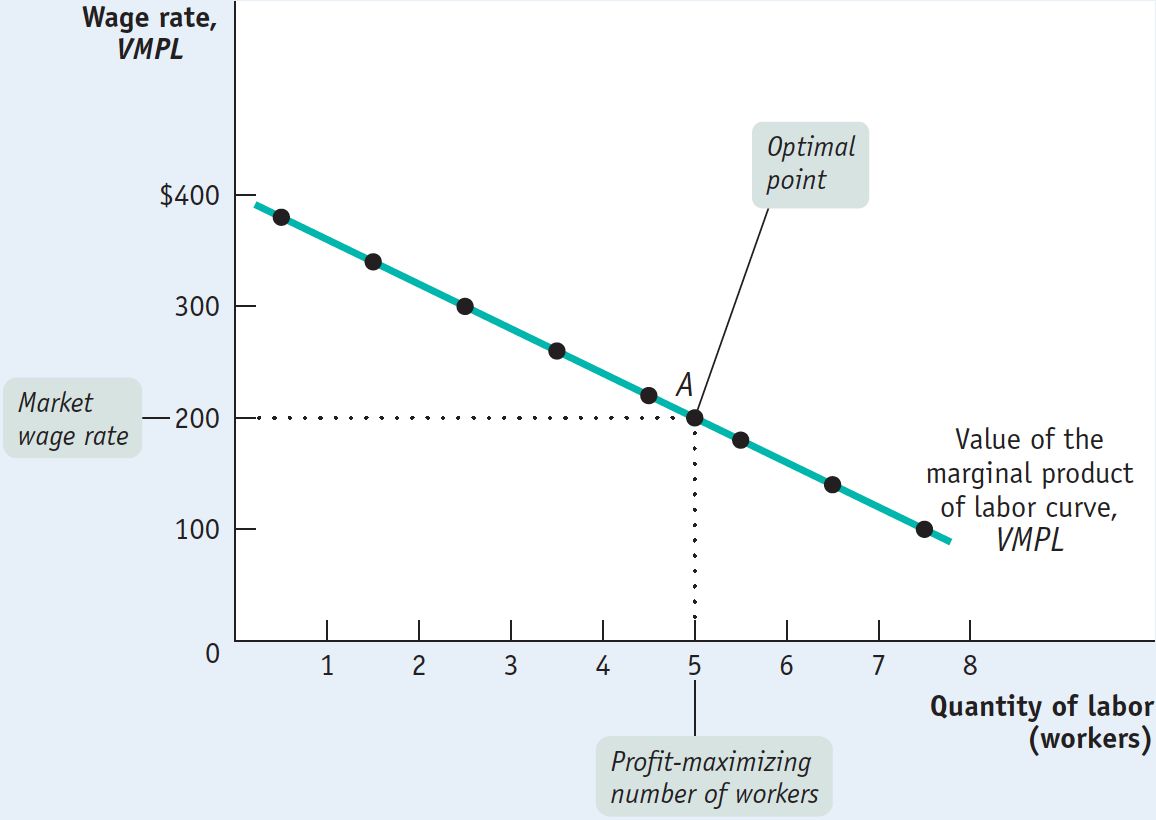
Looking at Table 19-2, we see that if George and Martha currently employ 3 workers, the value of the marginal product of an additional worker is $260. So if they employ an additional worker, they will increase the value of their production by $260 but increase their cost by only $200, yielding an increased profit of $60. In fact, a producer can always increase total profit by employing one more unit of a factor of production as long as the value of the marginal product produced by that unit exceeds its factor price.
Alternatively, suppose that George and Martha employ 8 workers. By reducing the number of workers to 7, they can save $200 in wages. In addition, the value of the marginal product of the last one, the 8th worker, was only $100. So, by reducing employment by one worker, they can increase profit by $200 − $100 = $100. In other words, a producer can always increase total profit by employing one less unit of a factor of production as long as the value of the marginal product produced by that unit is less than the factor price.
Using this method, we can see from Table 19-2 that the profit-
Now look again at the value of the marginal product curve in Figure 19-3. To determine the profit-

In this example, George and Martha have a small farm in which the potential employment level varies from 0 to 8 workers, and they hire workers up to the point at which the value of the marginal product of the last worker is greater than or equal to the wage rate. (To go beyond this point and hire workers for which the wage exceeds the value of the marginal product would reduce George and Martha’s profit.)
Suppose, however, that the firm in question is large and has the potential of hiring many workers. When there are many employees, the value of the marginal product of labor falls only slightly when an additional worker is employed. As a result, there will be some worker whose value of the marginal product almost exactly equals the wage rate. (In keeping with the George and Martha example, this means that some worker generates a value of the marginal product of approximately $200.) In this case, the firm maximizes profit by choosing a level of employment at which the value of the marginal product of the last worker hired equals (to a very good approximation) the wage rate.
In the interest of simplicity, we will assume from now on that firms use this rule to determine the profit-
Shifts of the Factor Demand Curve
As in the case of ordinary demand curves, it is important to distinguish between movements along the factor demand curve and shifts of the factor demand curve. What causes factor demand curves to shift? There are three main causes:
Changes in price of output
Changes in supply of other factors
Changes in technology
1. Changes in Price of Output Remember that factor demand is derived demand: if the price of the good that is produced with a factor changes, so will the value of the marginal product of the factor. That is, in the case of labor demand, if P changes, VMPL = P × MPL will change at any given level of employment.
Figure 19-4 illustrates the effects of changes in the price of wheat, assuming that $200 is the current wage rate. Panel (a) shows the effect of an increase in the price of wheat. This shifts the value of the marginal product of labor curve upward, because VMPL rises at any given level of employment. If the wage rate remains unchanged at $200, the optimal point moves from point A to point B: the profit-
19-4
Shifts of the Value of the Marginal Product Curve

Panel (b) shows the effect of a decrease in the price of wheat. This shifts the value of the marginal product of labor curve downward. If the wage rate remains unchanged at $200, the optimal point moves from point A to point C: the profit-
2. Changes in Supply of Other Factors Suppose that George and Martha acquire more land to cultivate—
In contrast, suppose George and Martha cultivate less land. This leads to a fall in the marginal product of labor at any given employment level. Each worker produces less wheat because each has less land to work with. As a result, the value of the marginal product of labor curve shifts downward—
3. Changes in Technology In general, the effect of technological progress on the demand for any given factor can go either way: improved technology can either increase or reduce the demand for a given factor of production.
How can technological progress reduce factor demand? Consider horses, which were once an important factor of production. The development of substitutes for horse power, such as automobiles and tractors, greatly reduced the demand for horses.
The usual effect of technological progress, however, is to increase the demand for a given factor by raising its productivity. So despite persistent fears that machinery would reduce the demand for labor, over the long run the U.S. economy has seen both large wage increases and large increases in employment. That’s because technological progress has raised labor productivity, and as a result increased the demand for labor.
The Marginal Productivity Theory of Income Distribution
We’ve now seen that each perfectly competitive producer in a perfectly competitive factor market maximizes profit by hiring labor up to the point at which its value of the marginal product is equal to its price—
Let’s start by assuming that the labor market is in equilibrium: at the current market wage rate, the number of workers that producers want to employ is equal to the number of workers willing to work. Thus, all employers pay the same wage rate, and each employer, whatever he or she is producing, employs labor up to the point at which the value of the marginal product of the last worker hired is equal to the market wage rate.
This situation is illustrated in Figure 19-5, which shows the value of the marginal product curves of two producers—
19-5
All Producers Face the Same Wage Rate
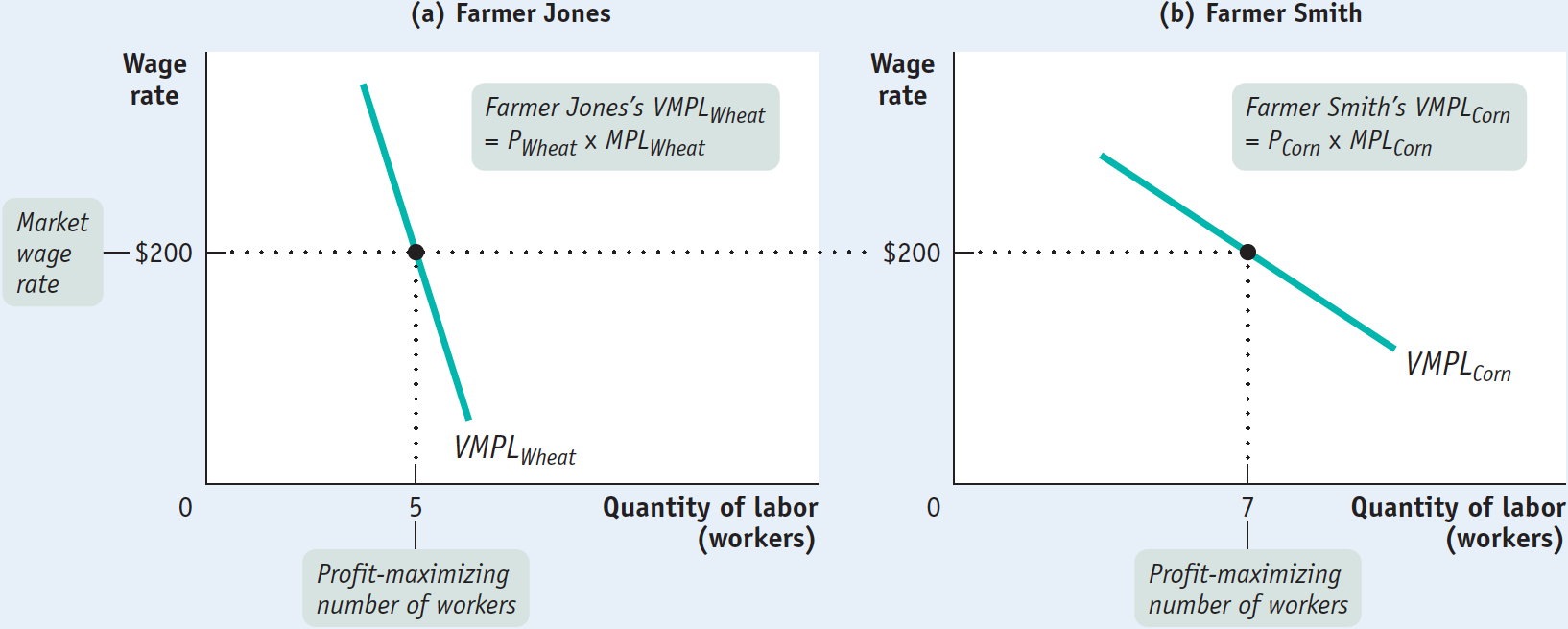
Figure 19-6 illustrates the labor market as a whole. The market labor demand curve, like the market demand curve for a good (shown in Figure 3-5), is the horizontal sum of all the individual labor demand curves of all the producers who hire labor. And recall that each producer’s individual labor demand curve is the same as his or her value of the marginal product of labor curve.
19-6
Equilibrium in the Labor Market
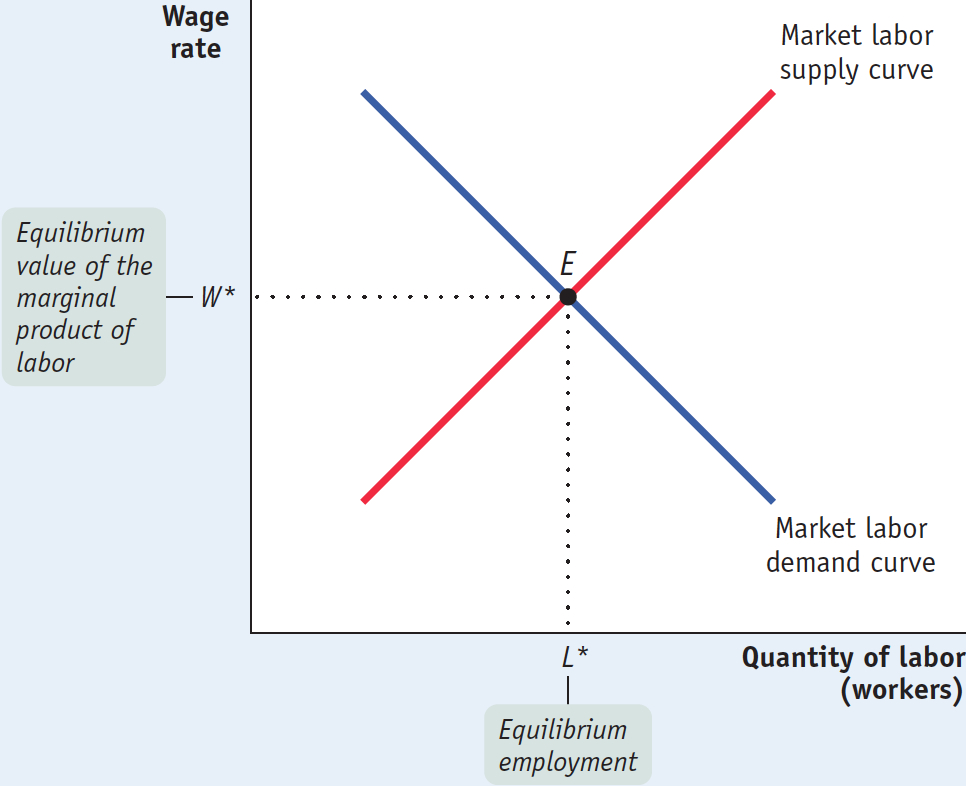
For now, let’s simply assume an upward-
The equilibrium value of the marginal product of a factor is the additional value produced by the last unit of that factor employed in the factor market as a whole.
And as we showed in the examples of the farms of George and Martha and of Farmer Jones and Farmer Smith (where the equilibrium wage rate is $200), each farm hires labor up to the point at which the value of the marginal product of labor is equal to the equilibrium wage rate. Therefore, in equilibrium, the value of the marginal product of labor is the same for all employers. So the equilibrium (or market) wage rate is equal to the equilibrium value of the marginal product of labor—
What we have just learned, then, is that the market wage rate is equal to the equilibrium value of the marginal product of labor. And the same is true of each factor of production: in a perfectly competitive market economy, the market price of each factor is equal to its equilibrium value of the marginal product. Let’s examine the markets for land and (physical) capital now. (From this point on, we’ll refer to physical capital as simply “capital.”)
The Markets for Land and Capital
If we maintain the assumption that the markets for goods and services are perfectly competitive, the result that we derived for the labor market also applies to other factors of production. Suppose, for example, that a farmer is considering whether to rent an additional acre of land for the next year. He or she will compare the cost of renting that acre with the value of the additional output generated by employing an additional acre—
What if the farmer already owns the land? We already saw the answer in Chapter 9, which dealt with economic decisions: even if you own land, there is an implicit cost—
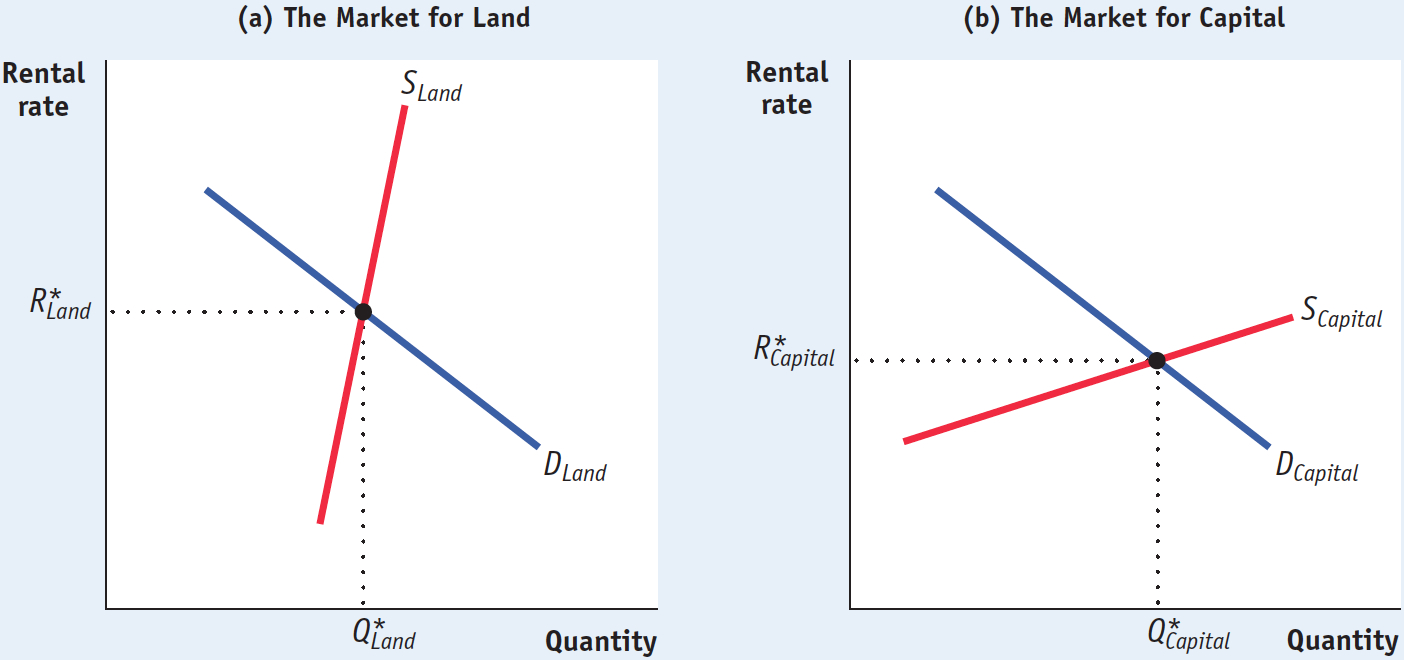
The same is true for capital. The explicit or implicit cost of using a unit of land or capital for a set period of time is called its rental rate. In general, a unit of land or capital is employed up to the point at which that unit’s value of the marginal product is equal to its rental rate over that time period. How are the rental rates for land and capital determined? By the equilibria in the land market and the capital market, of course. Figure 19-7 illustrates those outcomes.
19-7
Equilibria in the Land and Capital Markets
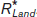 . Likewise, in a competitive capital market, each unit of capital will be paid the equilibrium value of the marginal product of capital,
. Likewise, in a competitive capital market, each unit of capital will be paid the equilibrium value of the marginal product of capital, 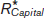 .
.The rental rate of either land or capital is the cost, explicit or implicit, of using a unit of that asset for a given period of time.
Panel (a) shows the equilibrium in the market for land. Summing over the individual demand curves for land of all producers gives us the market demand curve for land. Due to diminishing returns, the demand curve slopes downward, like the demand curve for labor. As we have drawn it, the supply curve of land is relatively steep and therefore relatively inelastic. This reflects the fact that finding new supplies of land for production is typically difficult and expensive—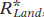 , and the equilibrium quantity of land employed in production,
, and the equilibrium quantity of land employed in production, 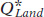 , are given by the intersection of the two curves.
, are given by the intersection of the two curves.
Panel (b) shows the equilibrium in the market for capital. In contrast to the supply curve for land, the supply curve for capital is relatively elastic. That’s because the supply of capital is relatively responsive to price: capital is paid for with funds that come from the savings of investors, and the amount of savings that investors make available is relatively responsive to the rental rate for capital. The equilibrium rental rate for capital, 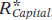 , and the equilibrium quantity of capital employed in production,
, and the equilibrium quantity of capital employed in production, 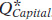 , are given by the intersection of the two curves.
, are given by the intersection of the two curves.
The Marginal Productivity Theory of Income Distribution
According to the marginal productivity theory of income distribution, every factor of production is paid its equilibrium value of the marginal product.
So we have learned that when the markets for goods and services and the factor markets are perfectly competitive, a factor of production will be employed up to the point at which its value of the marginal product is equal to its market equilibrium price. That is, it will be paid its equilibrium value of the marginal product. What does this say about the factor distribution of income? It leads us to the marginal productivity theory of income distribution, which says that each factor is paid the value of the output generated by the last unit of that factor employed in the factor market as a whole—
To understand why the marginal productivity theory of income distribution is important, look back at Figure 19-1, which shows the factor distribution of income in the United States, and ask yourself this question: who or what decided that labor would get 66% of total U.S. income? Why not 90% or 50%?
PITFALLS: GETTING MARGINAL PRODUCTIVITY THEORY RIGHT
GETTING MARGINAL PRODUCTIVITY THEORY RIGHT
It’s important to be careful about what the marginal productivity theory of income distribution says: it says that all units of a factor get paid the factor’s equilibrium value of the marginal product—
The most common source of error is to forget that the relevant value of the marginal product is the equilibrium value, not the value of the marginal products you calculate on the way to equilibrium. In looking at Table 19-2, you might be tempted to think that because the first worker has a value of the marginal product of $380, that worker is paid $380 in equilibrium. Not so: if the equilibrium value of the marginal product in the labor market is equal to $200, then all workers receive $200.
The answer, according to the marginal productivity theory of income distribution, is that the division of income among the economy’s factors of production isn’t arbitrary: it is determined by each factor’s marginal productivity at the economy’s equilibrium. The wage rate earned by all workers in the economy is equal to the increase in the value of output generated by the last worker employed in the economy-
Here we have assumed that all workers are of the same ability. (Similarly, we’ve assumed that all units of land and capital are equally productive.) But in reality workers differ considerably in ability.
Rather than thinking of one labor market for all workers in the economy, we can instead think of different markets for different types of workers, where workers are of equivalent ability within each market. For example, the market for computer programmers is different from the market for pastry chefs.
In the market for computer programmers, all participants are assumed to have equal ability; likewise for the market for pastry chefs. In this scenario, the marginal productivity theory of income distribution still holds. That is, when the labor market for computer programmers is in equilibrium, the wage rate earned by all computer programmers is equal to the market’s equilibrium value of the marginal product—
!worldview! ECONOMICS in Action: Help Wanted!
Help Wanted!
Hamill Manufacturing of Pennsylvania makes precision components for military helicopters and nuclear submarines. Their highly skilled senior machinists are well paid compared to other workers in manufacturing, earning nearly $70,000 in 2013, excluding benefits. Like most skilled machinists in the United States, Hamill’s machinists are very productive: according to the U.S. Census Annual Survey of Manufacturers, in 2010 the average skilled machinist generated approximately $137,000 in value added.
But there is a $67,000 difference between the salary paid to Hamill machinists and the value added they generate. Does this mean that the marginal productivity theory of income distribution doesn’t hold? Doesn’t the theory imply that machinists should be paid $137,000, the average value added that each one generates?

The answer is no, for two reasons. First, the $137,000 figure is averaged over all machinists currently employed. The theory says that machinists will be paid the value of the marginal product of the last machinist hired, and due to diminishing returns to labor, that value will be lower than the average over all machinists currently employed. Second, a worker’s equilibrium wage rate includes other costs, such as employee benefits, that have to be added to the $70,000 salary. The marginal productivity theory of income distribution says that workers are paid a wage rate, including all benefits, equal to the value of the marginal product.
You can see all these costs are present at Hamill. There the machinists have good benefits and job security, which add to their salary. Including these benefits, machinists’ total compensation will be equal to the value of the marginal product of the last machinist employed.
In Hamill’s case, there is yet another factor that explains the $67,000 gap: there are not enough machinists at the current wage rate. Although the company increased the number of employees from 85 in 2004 to 124 in 2013, they would like to hire more. Why doesn’t Hamill raise its wages in order to attract more skilled machinists? The problem is that the work they do is so specialized that it is hard to hire from the outside, even when the company raises wages as an inducement. To address this problem, Hamill has spent a significant amount of money training each new hire, approximately $130,000 plus the cost of benefits per trainee. (Unfortunately, training new hires has left Hamill vulnerable to poaching, which occurs when other companies that haven’t incurred the cost of training lure employees away by offering higher wages.) In the end, it does appear that the marginal productivity theory of income distribution holds.
Quick Review
In a perfectly competitive market economy, the price of the good multiplied by the marginal product of labor is equal to the value of the marginal product of labor: VMPL = P × MPL. A profit-
maximizing producer hires labor up to the point at which the value of the marginal product of labor is equal to the wage rate: VMPL = W. The value of the marginal product curve of labor slopes downward due to diminishing returns to labor in production. The market demand curve for labor is the horizontal sum of all the individual demand curves of producers in that market. It shifts for three reasons: changes in output price, changes in the supply of other factors, and technological progress.
As in the case of labor, producers will employ land or capital until the point at which its value of the marginal product is equal to its rental rate. According to the marginal productivity theory of income distribution, in a perfectly competitive economy each factor of production is paid its equilibrium value of the marginal product.
19-2
Question 19.2
In the following cases, state the direction of the shift of the demand curve for labor and what will happen, other things equal, to the market equilibrium wage rate and quantity of labor employed as a result.
Service industries, such as retailing and banking, experience an increase in demand. These industries use relatively more labor than nonservice industries.
As the demand for services increases, the price of services will rise. And as the price of the output produced by the industries increases, this shifts the VMPL curve upward—that is, the demand for labor rises. This results in an increase in both the equilibrium wage rate and the quantity of labor employed.
Due to overfishing, there is a fall in the amount of fish caught per day by commercial fishers; this decrease affects their demand for workers.
The fall in the catch per day means that the marginal product of labor in the industry declines. The VMPL curve shifts downward, generating a fall in the equilibrium wage rate and the equilibrium quantity of labor employed.
Question 19.3
Explain the following statement: “When firms in different industries all compete for the same workers, then the value of the marginal product of the last worker hired will be equal across all firms regardless of whether they are in different industries.”
When firms from different industries compete for the same workers, then each worker in the various industries will be paid the same equilibrium wage rate, W. And since, by the marginal productivity theory of income distribution, VMPL = P × MPL = W for the last worker hired in equilibrium, the last worker hired in each of these different industries will have the same value of the marginal product of labor.
Solutions appear at back of book.