Shifts of the Factor Demand Curve
As in the case of ordinary demand curves, it is important to distinguish between movements along the factor demand curve and shifts of the factor demand curve. What causes factor demand curves to shift? There are three main causes:
Changes in price of output
Changes in supply of other factors
Changes in technology
1. Changes in Price of Output Remember that factor demand is derived demand: if the price of the good that is produced with a factor changes, so will the value of the marginal product of the factor. That is, in the case of labor demand, if P changes, VMPL = P × MPL will change at any given level of employment.
Figure 19-4 illustrates the effects of changes in the price of wheat, assuming that $200 is the current wage rate. Panel (a) shows the effect of an increase in the price of wheat. This shifts the value of the marginal product of labor curve upward, because VMPL rises at any given level of employment. If the wage rate remains unchanged at $200, the optimal point moves from point A to point B: the profit-
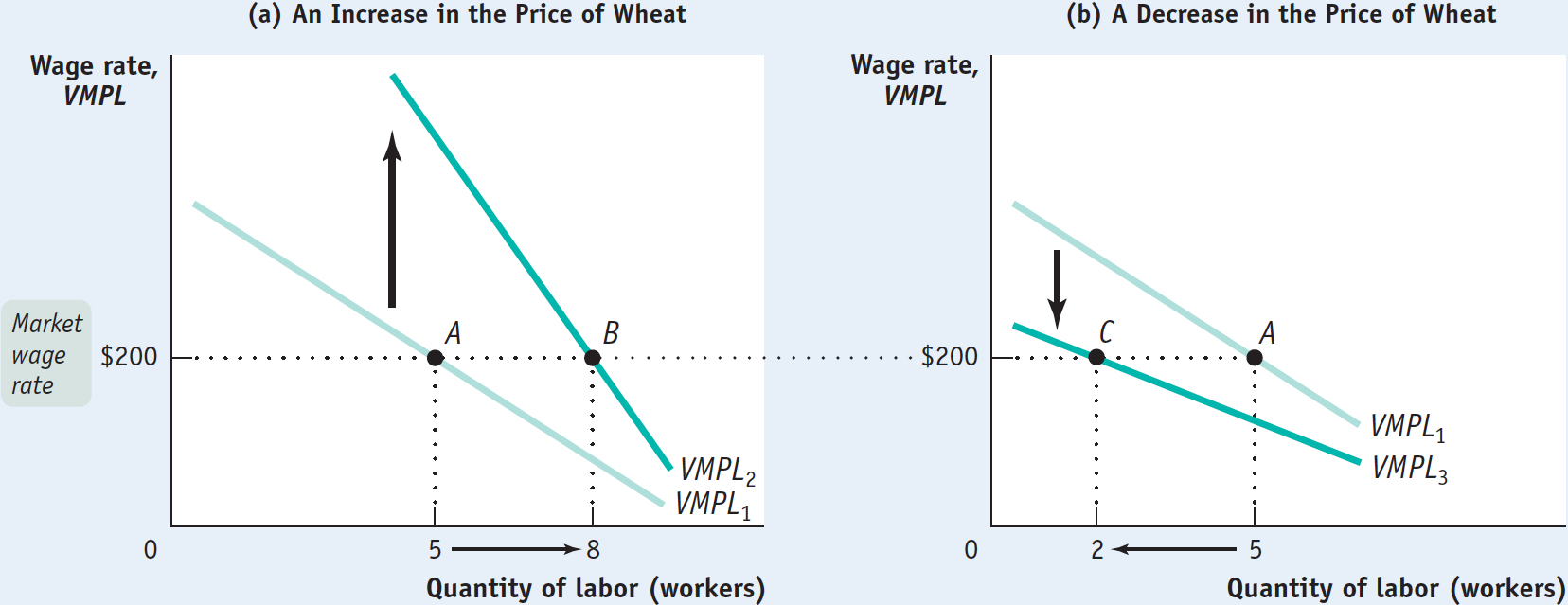
Panel (b) shows the effect of a decrease in the price of wheat. This shifts the value of the marginal product of labor curve downward. If the wage rate remains unchanged at $200, the optimal point moves from point A to point C: the profit-
2. Changes in Supply of Other Factors Suppose that George and Martha acquire more land to cultivate—
In contrast, suppose George and Martha cultivate less land. This leads to a fall in the marginal product of labor at any given employment level. Each worker produces less wheat because each has less land to work with. As a result, the value of the marginal product of labor curve shifts downward—
3. Changes in Technology In general, the effect of technological progress on the demand for any given factor can go either way: improved technology can either increase or reduce the demand for a given factor of production.
How can technological progress reduce factor demand? Consider horses, which were once an important factor of production. The development of substitutes for horse power, such as automobiles and tractors, greatly reduced the demand for horses.
The usual effect of technological progress, however, is to increase the demand for a given factor by raising its productivity. So despite persistent fears that machinery would reduce the demand for labor, over the long run the U.S. economy has seen both large wage increases and large increases in employment. That’s because technological progress has raised labor productivity, and as a result increased the demand for labor.
The Marginal Productivity Theory of Income Distribution
We’ve now seen that each perfectly competitive producer in a perfectly competitive factor market maximizes profit by hiring labor up to the point at which its value of the marginal product is equal to its price—
Let’s start by assuming that the labor market is in equilibrium: at the current market wage rate, the number of workers that producers want to employ is equal to the number of workers willing to work. Thus, all employers pay the same wage rate, and each employer, whatever he or she is producing, employs labor up to the point at which the value of the marginal product of the last worker hired is equal to the market wage rate.
This situation is illustrated in Figure 19-5, which shows the value of the marginal product curves of two producers—
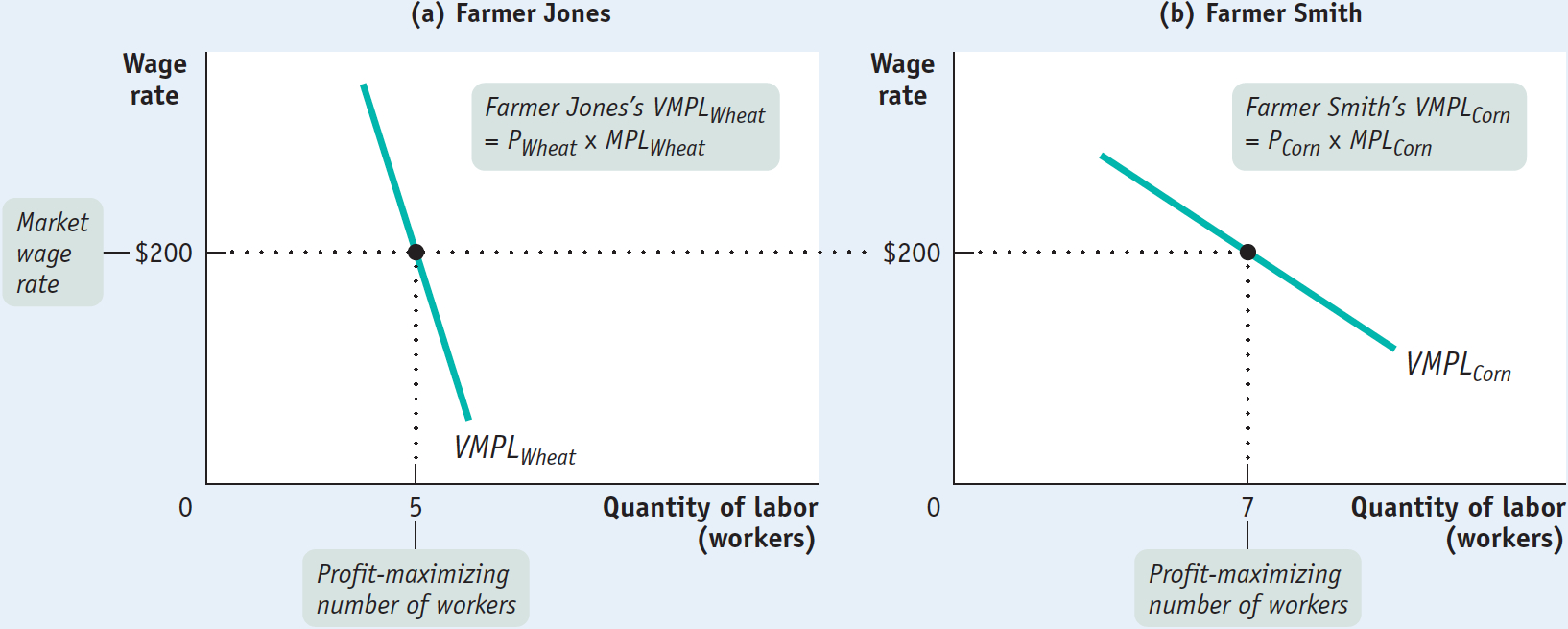
Figure 19-6 illustrates the labor market as a whole. The market labor demand curve, like the market demand curve for a good (shown in Figure 3-5), is the horizontal sum of all the individual labor demand curves of all the producers who hire labor. And recall that each producer’s individual labor demand curve is the same as his or her value of the marginal product of labor curve.
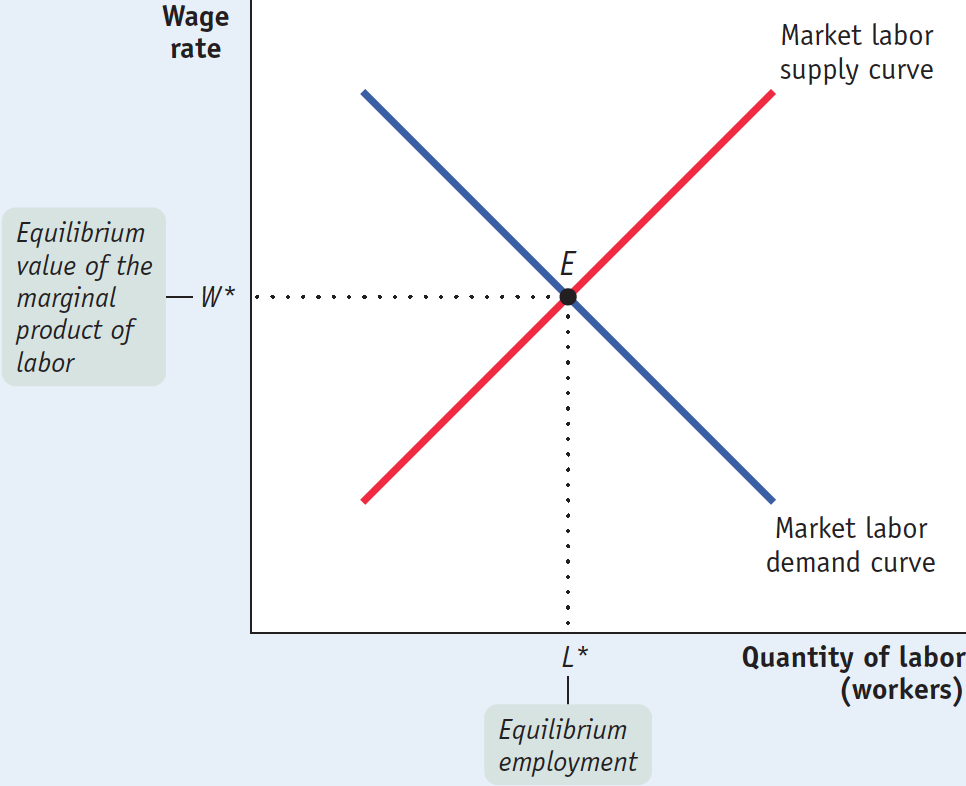
For now, let’s simply assume an upward-
The equilibrium value of the marginal product of a factor is the additional value produced by the last unit of that factor employed in the factor market as a whole.
And as we showed in the examples of the farms of George and Martha and of Farmer Jones and Farmer Smith (where the equilibrium wage rate is $200), each farm hires labor up to the point at which the value of the marginal product of labor is equal to the equilibrium wage rate. Therefore, in equilibrium, the value of the marginal product of labor is the same for all employers. So the equilibrium (or market) wage rate is equal to the equilibrium value of the marginal product of labor—
What we have just learned, then, is that the market wage rate is equal to the equilibrium value of the marginal product of labor. And the same is true of each factor of production: in a perfectly competitive market economy, the market price of each factor is equal to its equilibrium value of the marginal product. Let’s examine the markets for land and (physical) capital now. (From this point on, we’ll refer to physical capital as simply “capital.”)
The Markets for Land and Capital
If we maintain the assumption that the markets for goods and services are perfectly competitive, the result that we derived for the labor market also applies to other factors of production. Suppose, for example, that a farmer is considering whether to rent an additional acre of land for the next year. He or she will compare the cost of renting that acre with the value of the additional output generated by employing an additional acre—
What if the farmer already owns the land? We already saw the answer in Chapter 9, which dealt with economic decisions: even if you own land, there is an implicit cost—
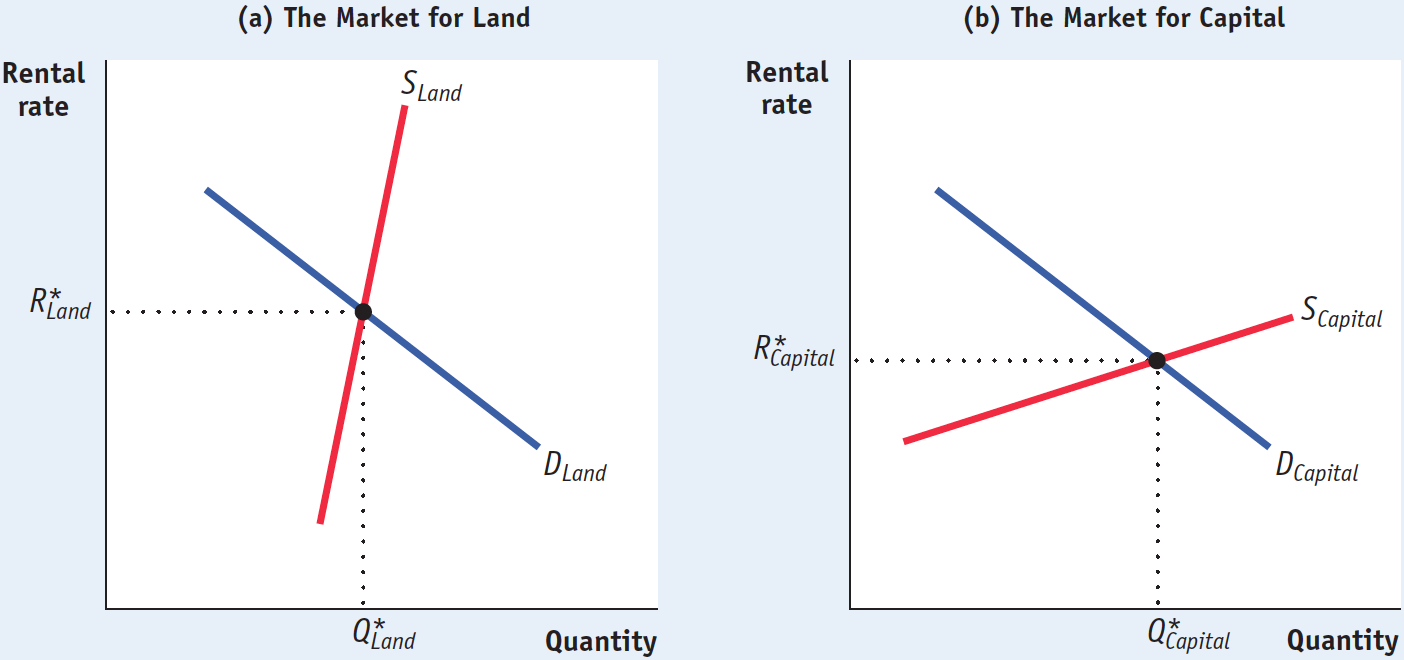
The same is true for capital. The explicit or implicit cost of using a unit of land or capital for a set period of time is called its rental rate. In general, a unit of land or capital is employed up to the point at which that unit’s value of the marginal product is equal to its rental rate over that time period. How are the rental rates for land and capital determined? By the equilibria in the land market and the capital market, of course. Figure 19-7 illustrates those outcomes.
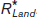 . Likewise, in a competitive capital market, each unit of capital will be paid the equilibrium value of the marginal product of capital,
. Likewise, in a competitive capital market, each unit of capital will be paid the equilibrium value of the marginal product of capital, 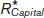 .
.The rental rate of either land or capital is the cost, explicit or implicit, of using a unit of that asset for a given period of time.
Panel (a) shows the equilibrium in the market for land. Summing over the individual demand curves for land of all producers gives us the market demand curve for land. Due to diminishing returns, the demand curve slopes downward, like the demand curve for labor. As we have drawn it, the supply curve of land is relatively steep and therefore relatively inelastic. This reflects the fact that finding new supplies of land for production is typically difficult and expensive—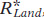 , and the equilibrium quantity of land employed in production,
, and the equilibrium quantity of land employed in production, 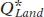 , are given by the intersection of the two curves.
, are given by the intersection of the two curves.
Panel (b) shows the equilibrium in the market for capital. In contrast to the supply curve for land, the supply curve for capital is relatively elastic. That’s because the supply of capital is relatively responsive to price: capital is paid for with funds that come from the savings of investors, and the amount of savings that investors make available is relatively responsive to the rental rate for capital. The equilibrium rental rate for capital, 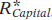 , and the equilibrium quantity of capital employed in production,
, and the equilibrium quantity of capital employed in production, 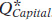 , are given by the intersection of the two curves.
, are given by the intersection of the two curves.
The Marginal Productivity Theory of Income Distribution
According to the marginal productivity theory of income distribution, every factor of production is paid its equilibrium value of the marginal product.
So we have learned that when the markets for goods and services and the factor markets are perfectly competitive, a factor of production will be employed up to the point at which its value of the marginal product is equal to its market equilibrium price. That is, it will be paid its equilibrium value of the marginal product. What does this say about the factor distribution of income? It leads us to the marginal productivity theory of income distribution, which says that each factor is paid the value of the output generated by the last unit of that factor employed in the factor market as a whole—
To understand why the marginal productivity theory of income distribution is important, look back at Figure 19-1, which shows the factor distribution of income in the United States, and ask yourself this question: who or what decided that labor would get 66% of total U.S. income? Why not 90% or 50%?
PITFALLS: GETTING MARGINAL PRODUCTIVITY THEORY RIGHT
PITFALLS
GETTING MARGINAL PRODUCTIVITY THEORY RIGHT
It’s important to be careful about what the marginal productivity theory of income distribution says: it says that all units of a factor get paid the factor’s equilibrium value of the marginal product—
The most common source of error is to forget that the relevant value of the marginal product is the equilibrium value, not the value of the marginal products you calculate on the way to equilibrium. In looking at Table 19-2, you might be tempted to think that because the first worker has a value of the marginal product of $380, that worker is paid $380 in equilibrium. Not so: if the equilibrium value of the marginal product in the labor market is equal to $200, then all workers receive $200.
The answer, according to the marginal productivity theory of income distribution, is that the division of income among the economy’s factors of production isn’t arbitrary: it is determined by each factor’s marginal productivity at the economy’s equilibrium. The wage rate earned by all workers in the economy is equal to the increase in the value of output generated by the last worker employed in the economy-
Here we have assumed that all workers are of the same ability. (Similarly, we’ve assumed that all units of land and capital are equally productive.) But in reality workers differ considerably in ability.
Rather than thinking of one labor market for all workers in the economy, we can instead think of different markets for different types of workers, where workers are of equivalent ability within each market. For example, the market for computer programmers is different from the market for pastry chefs.
In the market for computer programmers, all participants are assumed to have equal ability; likewise for the market for pastry chefs. In this scenario, the marginal productivity theory of income distribution still holds. That is, when the labor market for computer programmers is in equilibrium, the wage rate earned by all computer programmers is equal to the market’s equilibrium value of the marginal product—
!worldview! ECONOMICS in Action: Help Wanted!
Help Wanted!
Hamill Manufacturing of Pennsylvania makes precision components for military helicopters and nuclear submarines. Their highly skilled senior machinists are well paid compared to other workers in manufacturing, earning nearly $70,000 in 2013, excluding benefits. Like most skilled machinists in the United States, Hamill’s machinists are very productive: according to the U.S. Census Annual Survey of Manufacturers, in 2010 the average skilled machinist generated approximately $137,000 in value added.
But there is a $67,000 difference between the salary paid to Hamill machinists and the value added they generate. Does this mean that the marginal productivity theory of income distribution doesn’t hold? Doesn’t the theory imply that machinists should be paid $137,000, the average value added that each one generates?

The answer is no, for two reasons. First, the $137,000 figure is averaged over all machinists currently employed. The theory says that machinists will be paid the value of the marginal product of the last machinist hired, and due to diminishing returns to labor, that value will be lower than the average over all machinists currently employed. Second, a worker’s equilibrium wage rate includes other costs, such as employee benefits, that have to be added to the $70,000 salary. The marginal productivity theory of income distribution says that workers are paid a wage rate, including all benefits, equal to the value of the marginal product.
You can see all these costs are present at Hamill. There the machinists have good benefits and job security, which add to their salary. Including these benefits, machinists’ total compensation will be equal to the value of the marginal product of the last machinist employed.
In Hamill’s case, there is yet another factor that explains the $67,000 gap: there are not enough machinists at the current wage rate. Although the company increased the number of employees from 85 in 2004 to 124 in 2013, they would like to hire more. Why doesn’t Hamill raise its wages in order to attract more skilled machinists? The problem is that the work they do is so specialized that it is hard to hire from the outside, even when the company raises wages as an inducement. To address this problem, Hamill has spent a significant amount of money training each new hire, approximately $130,000 plus the cost of benefits per trainee. (Unfortunately, training new hires has left Hamill vulnerable to poaching, which occurs when other companies that haven’t incurred the cost of training lure employees away by offering higher wages.) In the end, it does appear that the marginal productivity theory of income distribution holds.
Quick Review
In a perfectly competitive market economy, the price of the good multiplied by the marginal product of labor is equal to the value of the marginal product of labor: VMPL = P × MPL. A profit-
maximizing producer hires labor up to the point at which the value of the marginal product of labor is equal to the wage rate: VMPL = W. The value of the marginal product curve of labor slopes downward due to diminishing returns to labor in production. The market demand curve for labor is the horizontal sum of all the individual demand curves of producers in that market. It shifts for three reasons: changes in output price, changes in the supply of other factors, and technological progress.
As in the case of labor, producers will employ land or capital until the point at which its value of the marginal product is equal to its rental rate. According to the marginal productivity theory of income distribution, in a perfectly competitive economy each factor of production is paid its equilibrium value of the marginal product.
19-2
Question 19.4
In the following cases, state the direction of the shift of the demand curve for labor and what will happen, other things equal, to the market equilibrium wage rate and quantity of labor employed as a result.
Service industries, such as retailing and banking, experience an increase in demand. These industries use relatively more labor than nonservice industries.
Due to overfishing, there is a fall in the amount of fish caught per day by commercial fishers; this decrease affects their demand for workers.
Question 19.5
Explain the following statement: “When firms in different industries all compete for the same workers, then the value of the marginal product of the last worker hired will be equal across all firms regardless of whether they are in different industries.”
Solutions appear at back of book.