The Economics of Risk Aversion
In general, people don’t like risk and are willing to pay a price to avoid it. Just ask the U.S. insurance industry, which collects more than $1 trillion in premiums every year. But what exactly is risk? And why don’t most people like it? To answer these questions, we need to look briefly at the concept of expected value and the meaning of uncertainty. Then we can turn to why people dislike risk.
Expectations and Uncertainty
The Lee family doesn’t know how big its medical bills will be next year. If all goes well, it won’t have any medical expenses at all. Let’s assume that there’s a 50% chance of that happening. But if family members require hospitalization or expensive drugs, they will face medical expenses of $10,000. Let’s assume that there’s also a 50% chance that these high medical expenses will materialize.
A random variable is a variable with an uncertain future value.
In this example—
The expected value of a random variable is the weighted average of all possible values, where the weights on each possible value correspond to the probability of that value occurring.
A state of the world is a possible future event.
To derive the general formula for the expected value of a random variable, we imagine that there are a number of different states of the world, possible future events. Each state is associated with a different realized value—
Let’s assume that P1 is the probability of state 1, P2 the probability of state 2, and so on. And you know the realized value of the random value in each state of the world: S1 in state 1, S2 in state 2, and so on. Let’s also assume that there are N possible states. Then the expected value of a random variable is:
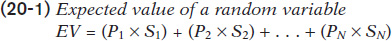
In the case of the Lee family, there are only two possible states of the world, each with a probability of 0.5.
Notice, however, that the Lee family doesn’t actually expect to pay $5,000 in medical bills next year. That’s because in this example there is no state of the world in which the family pays exactly $5,000. Either the family pays nothing, or it pays $10,000. So the Lees face considerable uncertainty about their future medical expenses.
But what if the Lee family can buy health insurance that will cover its medical expenses, whatever they turn out to be? Suppose, in particular, that the family can pay $5,000 up front in return for full coverage of whatever medical expenses actually arise during the coming year. Then the Lees’ future medical expenses are no longer uncertain for them: in return for $5,000—
Risk is uncertainty about future outcomes. When the uncertainty is about monetary outcomes, it becomes financial risk.
Yes, it would—
But before we study the market for insurance, we need to understand why people feel that risk is a bad thing, an attitude that economists call risk aversion. The source of risk aversion lies in a concept we first encountered in our analysis of consumer demand, back in Chapter 10: diminishing marginal utility.
The Logic of Risk Aversion
To understand how diminishing marginal utility gives rise to risk aversion, we need to look not only at the Lees’ medical costs but also at how those costs affect the income the family has left after medical expenses. Let’s assume the family knows that it will have an income of $30,000 next year. If the family has no medical expenses, it will be left with all of that income. If its medical expenses are $10,000, its income after medical expenses will be only $20,000. Since we have assumed that there is an equal chance of these two outcomes, the expected value of the Lees’ income after medical expenses is (0.5 × $30,000) + (0.5 × $20,000) = $25,000. At times we will simply refer to this as expected income.
Expected utility is the expected value of an individual’s total utility given uncertainty about future outcomes.
But as we’ll now see, if the family’s utility function has the shape typical of most families’, its expected utility—the expected value of its total utility given uncertainty about future outcomes—
To see why, we need to look at how total utility depends on income. Panel (a) of Figure 20-1 shows a hypothetical utility function for the Lee family, where total utility depends on income—
20-1
The Utility Function and Marginal Utility Curve of a Risk-
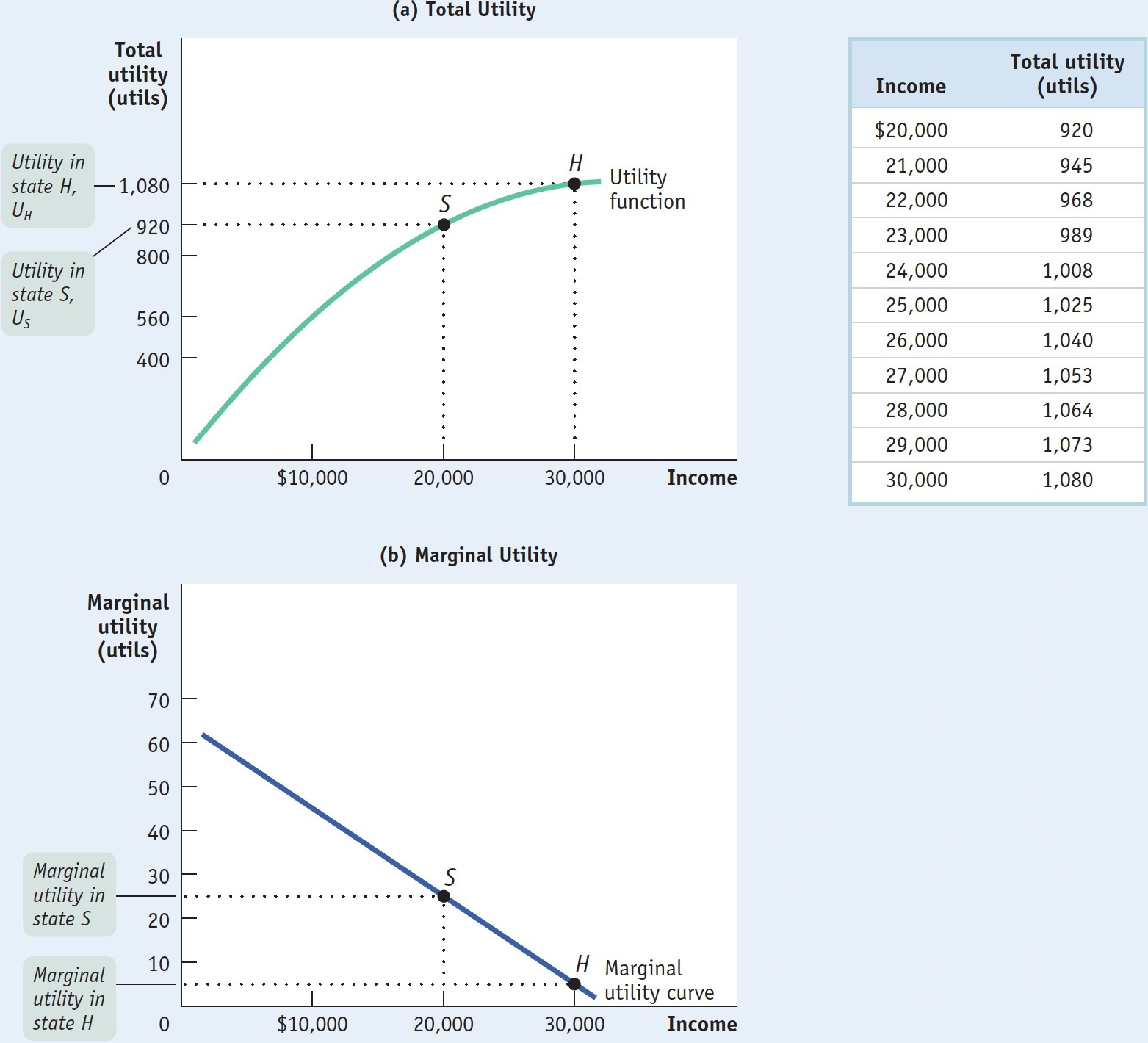
In Chapter 10 we applied the principle of diminishing marginal utility to individual goods and services: each successive unit of a good or service that a consumer purchases adds less to his or her total utility. The same principle applies to income used for consumption: each successive dollar of income adds less to total utility than the previous dollar. Panel (b) shows how marginal utility varies with income, confirming that marginal utility of income falls as income rises. As we’ll see in a moment, diminishing marginal utility is the key to understanding the desire of individuals to reduce risk.
To analyze how a person’s utility is affected by risk, economists start from the assumption that individuals facing uncertainty maximize their expected utility. We can use the data in Figure 20-1 to calculate the Lee family’s expected utility. We’ll first do the calculation assuming that the Lees have no insurance, and then we’ll recalculate it assuming that they have purchased insurance.
Without insurance, if the Lees are lucky and don’t incur any medical expenses, they will have an income of $30,000, generating total utility of 1,080 utils. But if they have no insurance and are unlucky, incurring $10,000 in medical expenses, they will have just $20,000 of their income to spend on consumption and total utility of only 920 utils. So without insurance, the family’s expected utility is (0.5 × 1,080) + (0.5 × 920) = 1,000 utils.
A premium is a payment to an insurance company in return for the insurance company’s promise to pay a claim in certain states of the world.
Now let’s suppose that an insurance company offers to pay whatever medical expenses the family incurs during the next year in return for a premium—a payment to the insurance company—
A fair insurance policy is an insurance policy for which the premium is equal to the expected value of the claim.
If the family purchases this fair insurance policy, the expected value of its income available for consumption is the same as it would be without insurance: $25,000—
Reading from the table in Figure 20-1, we see that this utility level is 1,025 utils. Or to put it a slightly different way, their expected utility with insurance is 1 × 1,025 = 1,025 utils, because with insurance they will receive a utility of 1,025 utils with a probability of 1. And this is higher than the level of expected utility without insurance—
Risk-
The calculations for this example are summarized in Table 20-1. This example shows that the Lees, like most people in real life, are risk-
20-1
The Effect of Fair Insurance on the Lee Family’s Income Available for Consumption and Expected Utility
|
Income in different states of the world |
||||
|---|---|---|---|---|
|
$0 in medical expenses (0.5 probability) |
$10,000 in medical expenses (0.5 probability) |
Expected value of income available for consumption |
Expected utility |
|
|
Without insurance |
$30,000 |
$20,000 |
(0.5 × $30,000) + (0.5 × $20,000) = $25,000 |
(0.5 × 1,080 utils) + (0.5 × 920 utils) = 1,000 utils |
|
With fair insurance |
$25,000 |
$25,000 |
(0.5 × $25,000) + (0.5 × $25,000) = $25,000 |
(0.5 × 1,025 utils) + (0.5 × 1,025 utils) = 1,025 utils |
TABLE 20-
You might think that this result depends on the specific numbers we have chosen. In fact, however, the proposition that purchase of a fair insurance policy increases expected utility depends on only one assumption: diminishing marginal utility. The reason is that with diminishing marginal utility, a dollar gained when income is low adds more to utility than a dollar gained when income is high.
That is, having an additional dollar matters more when you are facing hard times than when you are facing good times. And as we will shortly see, a fair insurance policy is desirable because it transfers a dollar from high-
But first, let’s see how diminishing marginal utility leads to risk aversion by examining expected utility more closely. In the case of the Lee family, there are two states of the world; let’s call them H and S, for healthy and sick. In state H the family has no medical expenses; in state S it has $10,000 in medical expenses. Let’s use the symbols UH and US to represent the Lee family’s total utility in each state. Then the family’s expected utility is:
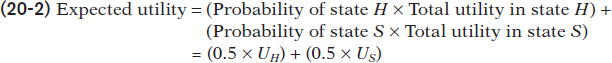
The fair insurance policy reduces the family’s income available for consumption in state H by $5,000, but it increases it in state S by the same amount. As we’ve just seen, we can use the utility function to directly calculate the effects of these changes on expected utility. But as we have also seen in many other contexts, we gain more insight into individual choice by focusing on marginal utility.
To use marginal utility to analyze the effects of fair insurance, let’s imagine introducing the insurance a bit at a time, say in 5,000 small steps. At each of these steps, we reduce income in state H by $1 and simultaneously increase income in state S by $1. At each of these steps, total utility in state H falls by the marginal utility of income in that state but total utility in state S rises by the marginal utility of income in that state.
Now look again at panel (b) of Figure 20-1, which shows how marginal utility varies with income. Point S shows marginal utility when the Lee family’s income is $20,000; point H shows marginal utility when income is $30,000. Clearly, marginal utility is higher when income after medical expenses is low. Because of diminishing marginal utility, an additional dollar of income adds more to total utility when the family has low income (point S) than when it has high income (point H).
This tells us that the gain in expected utility from increasing income in state S is larger than the loss in expected utility from reducing income in state H by the same amount. So at each step of the process of reducing risk, by transferring $1 of income from state H to state S, expected utility increases. This is the same as saying that the family is risk-
Almost everyone is risk-
Panel (a) of Figure 20-2 shows how each individual’s total utility would be affected by the change in income. Danny would gain very few utils from a rise in income, which moves him from N to HD, but lose a large number of utils from a fall in income, which moves him from N to LD. That is, he is highly risk-
20-2
Differences in Risk Aversion
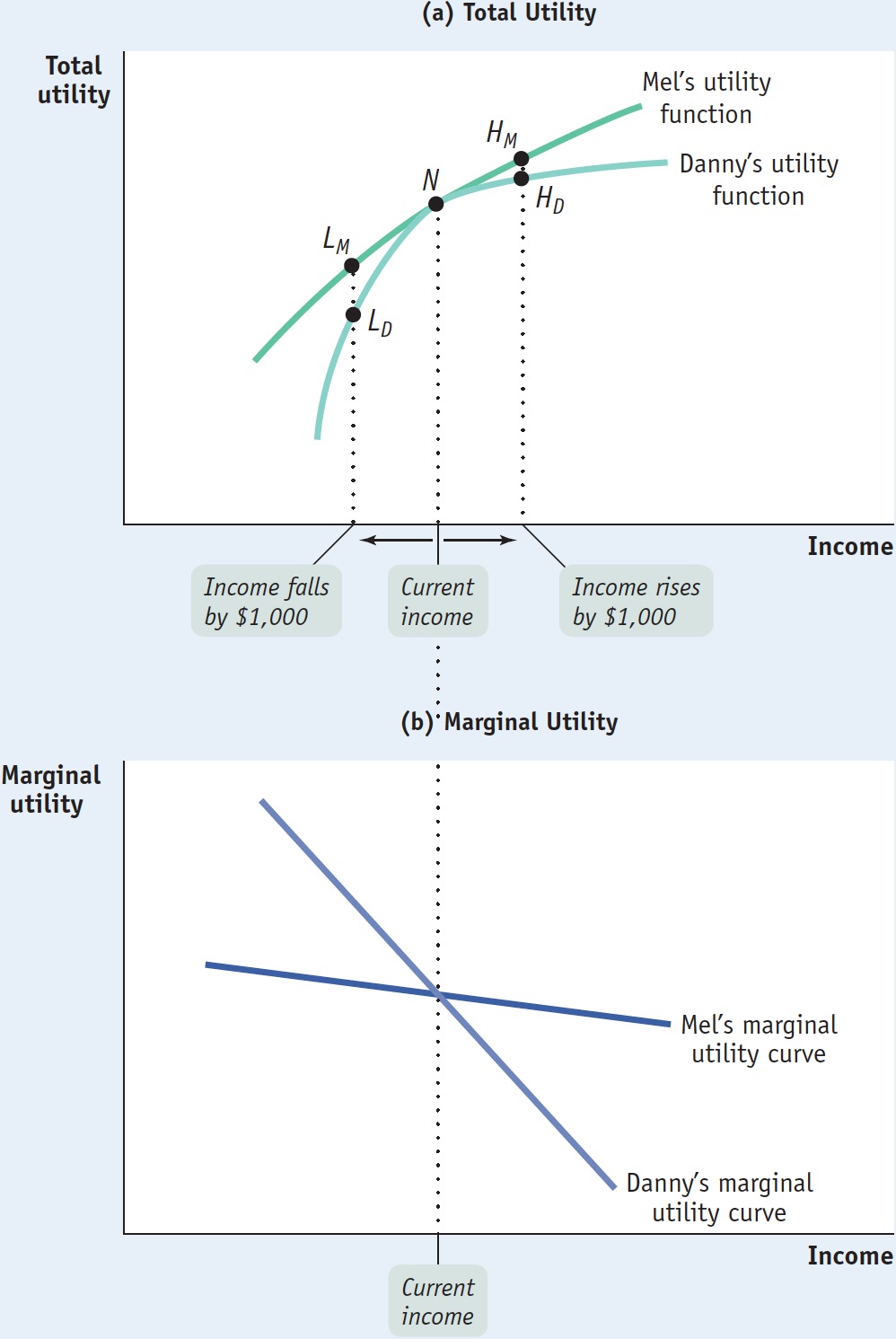
A risk-
Mel, though, as shown in panel (a), would gain almost as many utils from higher income, which moves him from N to HM, as he would lose from lower income, which moves him from N to LM. He is barely risk-
The Paradox of Gambling
If most people are risk-
After all, a casino doesn’t even offer gamblers a fair gamble: all the games in any gambling facility are designed so that, on average, the casino makes money. So why would anyone play their games?
You might argue that the gambling industry caters to the minority of people who are actually the opposite of risk-

Instead, most of them are ordinary people who have health and life insurance and who wear seat belts. In other words, they are risk-
So why do people gamble? Presumably because they enjoy the experience.
Also, gambling may be one of those areas where the assumption of rational behavior goes awry. Psychologists have concluded that gambling can be addictive in ways that are not that different from the addictive effects of drugs. Taking dangerous drugs is irrational; so is excessive gambling. Alas, both happen all the same.
Individuals differ in risk aversion for two main reasons: differences in preferences and differences in initial income or wealth.
Differences in preferences. Other things equal, people simply differ in how much their marginal utility is affected by their level of income. Someone whose marginal utility is relatively unresponsive to changes in income will be much less sensitive to risk. In contrast, someone whose marginal utility depends greatly on changes in income will be much more risk-
averse. Differences in initial income or wealth. The possible loss of $1,000 makes a big difference to a family living below the poverty threshold; it makes very little difference to someone who earns $1 million a year. In general, people with whigh incomes or high wealth will be less risk-
averse.
Differences in risk aversion have an important consequence: they affect how much an individual is willing to pay to avoid risk.
Paying to Avoid Risk
The risk-
Will the Lee family still want to purchase an “unfair” insurance policy—
It depends on the size of the premium. Look again at Table 20-1. We know that without insurance expected utility is 1,000 utils and that insurance costing $5,000 raises expected utility to 1,025 utils. If the premium were $6,000, the Lees would be left with an income of $24,000, which, as you can see from Figure 20-1, would give them a total utility of 1,008 utils—
PITFALLS: BEFORE THE FACT VERSUS AFTER THE FACT
BEFORE THE FACT VERSUS AFTER THE FACT
Why is an insurance policy different from a doughnut?
No, it’s not a riddle. Although the supply and demand for insurance behave like the supply and demand for any good or service, the payoff is very different. When you buy a doughnut, you know what you’re going to get; when you buy insurance, by definition you don’t know what you’re going to get. If you bought car insurance and then didn’t have an accident, you got nothing from the policy, except peace of mind, and might wish that you hadn’t bothered. But if you did have an accident, you probably would be glad that you bought insurance that covered the cost.
This means we have to be careful in assessing the rationality of insurance purchases (or, for that matter, any decision made in the face of uncertainty). After the fact-
One highly successful Wall Street investor told us that he never looks back-
This example shows that risk-
ECONOMICS in Action: Warranties
Warranties

Many expensive consumer goods—
Why do manufacturers offer warranties? Part of the answer is that warranties signal to consumers that the goods are of high quality. But mainly warranties are a form of consumer insurance. For many people, the cost of repairing or replacing an expensive item like a refrigerator—
So a warranty that covers the cost of repair or replacement increases the consumer’s expected utility, even if the cost of the warranty is greater than the expected future claim paid by the manufacturer.
Quick Review
The expected value of a random variable is the weighted average of all possible values, where the weight corresponds to the probability of a given value occurring.
Uncertainty about states of the world entails risk, or financial risk when there is an uncertain monetary outcome. When faced with uncertainty, consumers choose the option yielding the highest level of expected utility.
Most people are risk-
averse: they would be willing to purchase a fair insurance policy in which the premium is equal to the expected value of the claim.Risk aversion arises from diminishing marginal utility. Differences in preferences and in income or wealth lead to differences in risk aversion.
Depending on the size of the premium, a risk-
averse person may be willing to purchase an “unfair” insurance policy with a premium larger than the expected claim. The greater your risk aversion, the greater the premium you are willing to pay. A risk- neutral person is unwilling to pay any premium to avoid risk.
20-1
Question 20.1
Compare two families who own homes near the coast in Florida. Which family is likely to be more risk-
averse— (i) a family with income of $2 million per year or (ii) a family with income of $60,000 per year? Would either family be willing to buy an “unfair” insurance policy to cover losses to their Florida home? Income
Total utility (utils)
$22,000
850
25,000
1,014
26,000
1,056
35,000
1,260
The family with the lower income is likely to be more risk-averse. In general, higher income or wealth results in lower degrees of risk aversion, due to diminishing marginal utility. Both families may be willing to buy an “unfair” insurance policy. Most insurance policies are “unfair” in that the expected claim is less than the premium. The degree to which a family is willing to pay more than an expected claim for insurance depends on the family’s degree of risk aversion.
Question 20.2
Karma’s income next year is uncertain: there is a 60% probability she will make $22,000 and a 40% probability she will make $35,000. The accompanying table shows some income and utility levels for Karma.
What is Karma’s expected income? Her expected utility?
Karma’s expected income is the weighted average of all possible values of her income, weighted by the probabilities with which she earns each possible value of her income. Since she makes $22,000 with a probability of 0.6 and $35,000 with a probability of 0.4, her expected income is (0.6 × $22,000) + (0.4 × $35,000) = $13,200 + $14,000 = $27,200. Her expected utility is simply the expected value of the total utilities she will experience. Since with a probability of 0.6 she will experience a total utility of 850 utils (the utility to her from making $22,000), and with a probability of 0.4 she will experience a total utility of 1,260 utils (the utility to her from making $35,000), her expected utility is (0.6 × 850 utils) + (0.4 × 1,260 utils) = 510 utils + 504 utils = 1,014 utils.
What certain income level leaves her as well off as her uncertain income? What does this imply about Karma’s attitudes toward risk? Explain.
If Karma makes $25,000 for certain, she experiences a utility level of 1,014 utils. From the answer to part a, we know that this leaves her equally as well off as when she has a risky expected income of $27,200. Since Karma is indifferent between a risky expected income of $27,200 and a certain income of $25,000, you can conclude that she would prefer a certain income of $27,200 to a risky expected income of $27,200. That is, she would definitely be willing to reduce the risk she faces when this reduction in risk leaves her expected income unchanged. In other words, Karma is risk-averse.
Would Karma be willing to pay some amount of money greater than zero for an insurance policy that guarantees her an income of $26,000? Explain.
Yes. Karma experiences a utility level of 1,056 utils when she has a certain income of $26,000. This is higher than the expected utility level of 1,014 utils generated by a risky expected income of $27,200. So Karma is willing to pay a premium to guarantee a certain income of $26,000.
Solutions appear at back of book.