1.3 Module 58: The Time Value of Money

Shutterstock

In the previous module we learned that present value helps to explain why the demand curve for loanable funds slopes downward. In this module, we’ll look more closely at present value, and consider how it is put to use by individuals and firms when making financial decisions.

The Concept of Present Value

Individuals and firms are often faced with financial decisions that will have consequences long into the future. For example, when you decided to attend college, you committed yourself to years of study, which you expect will pay off for the rest of your life. So the decision to attend college is a decision to embark on a long-term project.

The basic rule in deciding whether or not to undertake a project is that you should compare the benefits of that project with its costs, implicit as well as explicit. But making these comparisons can sometimes be difficult because the benefits and costs of a project may not arrive at the same time.

This is true of the saving and investment decisions made by individuals: these decisions also have benefits and costs that do not arrive at the same time. For example, if you save more today the benefit is that you will earn interest and have more accumulated wealth at a later date. The cost is that you have less income available for consumption today.

Likewise, when a firm decides to invest in new physical capital today, it is anticipating benefits like increased output, productivity, and profit that will come later, possibly much later. But how, specifically, is time an issue in economic decision making?

Borrowing, Lending, and Interest

In general, having a dollar today is worth more than having a dollar a year from now. To see why, let’s consider two examples.

First, suppose that you get a new job that comes with a $1,000 bonus, which will be paid at the end of the first year. But you would like to spend the extra money now—say, on new clothes for work. Can you do that?

The answer is yes—you can borrow money today and use the bonus to repay the debt a year from now. But if that is your plan, you cannot borrow the full $1,000 today. You must borrow less than that because a year from now you will have to repay the amount borrowed plus interest.

Now consider a different scenario. Suppose that you are paid a bonus of $1,000 today, and you decide that you don’t want to spend the money until a year from now. What do you do with it? You may decide to put it in the bank; in effect, you would be lending the $1,000 to the bank, which in turn lends it out to its customers who wish to borrow. At the end of a year, you will get more than $1,000 back—you will receive the $1,000 plus the interest earned.

All of this means that having $1,000 today is worth more than having $1,000 a year from now. As any borrower and lender know, this is what allows a lender to charge a borrower interest on a loan: borrowers are willing to pay interest in order to have money today rather than waiting until they acquire that money later on.

Most interest rates are stated as the percentage of the borrowed amount that must be paid to the lender for each year of the loan. Whether money is actually borrowed for 1 month or 10 years, and regardless of the amount, the same principle applies: money in your pocket today is worth more than money in your pocket tomorrow. To keep things simple in the discussions that follow, we’ll restrict ourselves to examples of 1-year loans of $1.

Because the value of money depends on when it is paid or received, you can’t evaluate a project by simply adding up the costs and benefits when those costs and benefits arrive at different times. You must take time into account when evaluating the project because $1 that is paid to you today is worth more than $1 that is paid to you a year from now. Similarly, $1 that you must pay today is more burdensome than $1 that you must pay next year.

Fortunately, there is a simple way to adjust for these complications so that we can correctly compare the value of dollars received and paid out at different times.

Next we’ll see how the interest rate can be used to convert future benefits and costs into what economists call present values. By using present values when evaluating a project, you can evaluate a project as if all relevant costs and benefits were occurring today rather than at different times. This allows people to “factor out” the complications created by time. We’ll start by defining the concept of present value.

Defining Present Value

Having a dollar today is worth more than having a dollar a year from now.

Stockphoto/Thinkstock

The key to the concept of present value is to understand that the interest rate can be used to compare the value of a dollar realized today with the value of a dollar realized later. Why the interest rate? Because the interest rate correctly measures the cost of delaying the receipt of a dollar of benefit and, correspondingly, the benefit of delaying the payment of a dollar of cost.

Let’s illustrate this with some examples.

Suppose that you are evaluating whether or not to take a job in which your employer promises to pay you a bonus at the end of the first year. What is the value to you today of $1 of bonus money to be paid one year in the future? A slightly different way of asking the same question: what amount would you be willing to accept today as a substitute for receiving $1 one year from now?

To answer this question, begin by observing that you need less than $1 today in order to be assured of having $1 one year from now. Why? Because any money that you have today can be lent out at interest—say, by depositing it in a bank account so that the bank can then lend it out to its borrowers. This turns any amount you have today into a greater sum at the end of the year.

Let’s work this out mathematically. We’ll use the symbol r to represent the interest rate, expressed in decimal terms—that is, if the interest rate is 10%, then r = 0.10. If you lend out $X, at the end of a year you will receive your $X back, plus the interest on your $X, which is $X × r. Thus, at the end of the year you will receive:

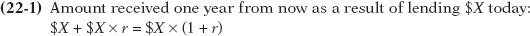
The next step is to find out how much you would have to lend out today to have $1 a year from now. To do that, we just need to set Equation 22-1 equal to $1 and solve for $X. That is, we solve the following equation for $X:

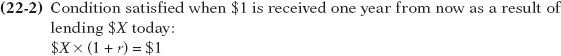
Rearranging Equation 22-2 to solve for $X, the amount you need today in order to receive $1 one year from now is:

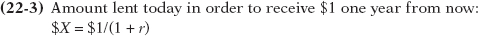
This means that you would be willing to accept today the amount $X defined by Equation 22-3 for every $1 to be paid to you one year from now. The reason is that if you were to lend out $X today, you would be assured of receiving $1 one year from now. Returning to our original question, this also means that if someone promises to pay you a sum of money one year in the future, you are willing to accept $X today in place of every $1 to be paid one year from now.

Now let’s solve Equation 22-3 for the value of $X. To do this we simply need to use the actual value of r (a value determined by the financial markets). Let’s assume that the actual value of r is 10%, which means that r = 0.10. In that case:

So you would be willing to accept $0.91 today in exchange for every $1 to be paid to you one year from now. Economists refer to $X as the present value of $1. Note that the present value of any given amount will change as the interest rate changes.

To see that this technique works for evaluating future costs as well as evaluating future benefits, consider the following example. Suppose you enter into an agreement that obliges you to pay $1 one year from now—say, to pay off a car loan from your parents when you graduate in a year. How much money would you need today to ensure that you have $1 in a year? The answer is $X, the present value of $1, which in our example is $0.91.

The present value of a given amount will change as the interest rate changes.

Imagebroker/Alamy

The reason $0.91 is the right answer is that if you lend it out for one year at an interest rate of 10%, you will receive $1 in return at the end. So if, for example, you must pay back $5,000 one year from now, then you need to deposit $5,000 × 0.91 = $4,550 into a bank account today earning an interest rate of 10% in order to have $5,000 one year from now. (There is a slight discrepancy due to rounding.) In other words, today you need to have the present value of $5,000, which equals $4,550, in order to be assured of paying off your debt in a year.

These examples show us that the present value concept provides a way to calculate the value today of $1 that is realized in a year—regardless of whether that $1 is realized as a benefit (the bonus) or a cost (the car loan payback). To evaluate a project today that has benefits, costs, or both to be realized in a year, we just use the relevant interest rate to convert those future dollars into their present values. In that way we have “factored out” the complication that time creates for decision making.

Below we will use the present value concept to evaluate a project. But before we do that, it is worthwhile to note that the present value method can be used for projects in which the $1 is realized more than a year later—say, two, three, or even more years. Let’s consider a project that will pay $1 two years from today. What is the value to you today of $1 received two years into the future? We can find the answer to that question by expanding our formula for present value.

Let’s call $V the amount of money that would need to be lent today at an interest rate of r in order to have $1 in two years. So if an individual or firm lends $V today, it will receive $V × (1 + r) in one year. And if it relends that sum for another year, it will receive $V × (1 + r) × (1 + r) = $V × (1 + r)² at the end of the second year. At the end of two years, $V will be worth $V × (1 + r)². In other words:

Amount received in two years from lending $V = $V × (1 + r) × (1 + r) = $V × (1 + r)² and so on. For example, if r = 0.10, then $V × (1.10)² = $V × 1.21.

Now we are ready to answer the question of what $1 realized two years in the future is worth today. In order for the amount lent today, $V, to be worth $1 two years from now, it must satisfy this formula:

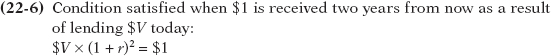
Rearranging Equation 22-6, we can solve for $V:

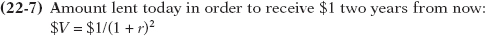
Given r = 0.10 and using Equation 22-7, we arrive at $V = $1/1.21 = $0.83. So, when the interest rate is 10%, $1 realized two years from today is worth $0.83 today because by lending out $0.83 today the individual or firm can be assured of having $1 in two years. And that means that the present value of $1 realized two years into the future is $0.83.

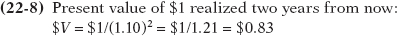
From this example we can see how the present value concept can be expanded to a number of years even greater than two. If we ask what the present value is of $1 realized any number of years, represented by N, into the future, the answer is given by a generalization of the present value formula: it is equal to $1/(1 + r)^N.

Using Present Value

Suppose an individual or firm has to choose one of three hypothetical projects to undertake. Project A costs nothing and has an immediate payoff of $100. Project B requires a payment of $10 today in order to receive $115 a year from now. Project C offers an immediate payoff of $119 but requires a payment of $20 a year from now. We’ll assume that the annual interest rate is 10%—that is, r = 0.10.

The problem in evaluating these three projects is that their costs and benefits are realized at different times. That is, of course, where the concept of present value becomes extremely helpful: by using present value to convert any dollars realized in the future into today’s value, we factor out the issue of time. Appropriate comparisons can be made using the net present value of a project—the present value of current and future benefits minus the present value of current and future costs. The best project to undertake is the one with the highest net present value.

Table 58-1 shows how to calculate net present value for each of the three projects. The second and third columns show how many dollars are realized and when they are realized; costs are indicated by a minus sign. The fourth column shows the equations used to convert the flows of dollars into their present value, and the fifth column shows the actual amounts of the total net present value for each of the three projects.

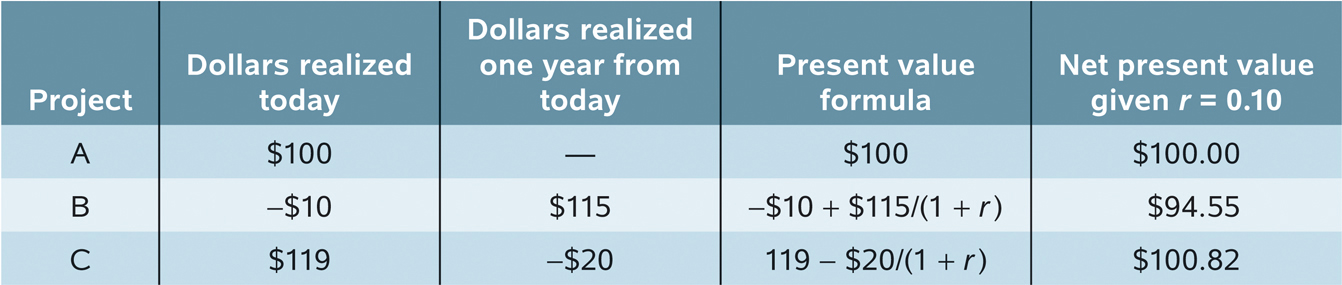
For instance, to calculate the net present value of project B, we need to calculate the present value of $115 received in one year. The present value of $1 received in one year would be $1/(1 + r). So the present value of $115 is equal to 115 × $1/(1 + r); that is, $115/(1 + r). The net present value of project B is the present value of today’s and future benefits minus the present value of today’s and future costs: −$10 + $115/(1 + r).

From the fifth column, we can immediately see which is the preferred project—it is project C. That’s because it has the highest net present value, $100.82, which is higher than the net present value of project A ($100) and much higher than the net present value of project B ($94.55).

This example shows how important the concept of present value is. If we had failed to use the present value calculations and instead simply added up the dollars generated by each of the three projects, we could have easily been misled into believing that project B was the best project and project C was the worst.

HOW BIG IS THAT JACKPOT, ANYWAY?

For a clear example of present value at work, consider the case of lottery jackpots.

David Gould/Photographers Choice RF/Getty Images

On March 30, 2012, Mega Millions set a record for the largest jackpot ever in North America, with a payout of $656 million. Well, sort of. That $656 million was available only if the winner chose to take his or her winnings in the form of an “annuity,” consisting of an annual payment for the next 26 years. If the winner wanted cash up front, the jackpot was only $474 million and change.

Why was Mega Millions so stingy about quick payoffs? It was all a matter of present value. If the winner had been willing to take the annuity, the lottery would have invested the jackpot money, buying U.S. government bonds (in effect lending the money to the federal government). The money would have been invested in such a way that the investments would pay just enough to cover the annuity. This worked, of course, because at the interest rates prevailing at the time, the present value of a $656 million annuity spread over 26 years was just about $474 million. To put it another way, the opportunity cost to the lottery of that annuity in present value terms was $474 million.

So why didn’t they just call it a $474 million jackpot? Well, $656 million sounds more impressive! But receiving $656 million over 26 years is essentially the same as receiving $474 million today.

Module 58 Review

Check Your Understanding