1.3 62The Income–Expenditure Model

WHAT YOU WILL LEARN
 How planned aggregate spending determines income–
How planned aggregate spending determines income–expenditure equilibrium  How the inventory adjustment process moves the economy to a new equilibrium after a change in planned aggregate spending
How the inventory adjustment process moves the economy to a new equilibrium after a change in planned aggregate spending
Using the Income–Expenditure Model
Earlier in this section, we described how autonomous changes in spending—
Before we begin, let’s quickly recap the assumptions underlying the multiplier process.
- Changes in overall spending lead to changes in aggregate output. We assume that producers are willing to supply additional output at a fixed price level. As a result, changes in spending translate into changes in output rather than moves of the overall price level up or down. A fixed aggregate price level also implies that there is no difference between nominal GDP and real GDP. So we can use the two terms interchangeably in this module.
- The interest rate is fixed. As we’ll see, the model we examine here can still be used to study the effects of a change in the interest rate.
- Taxes, government transfers, and government purchases are all zero.
- Exports and imports are both zero.
Planned Aggregate Spending and Real GDP
In an economy with no government and no foreign trade, there are only two sources of aggregate spending: consumer spending, C, and investment spending, I. And since we assume that there are no taxes or transfers, aggregate disposable income is equal to GDP (which, since the aggregate price level is fixed, is the same as real GDP): the total value of final sales of goods and services ultimately accrues to households as income. So in this highly simplified economy, there are two basic equations of national income accounting:
(62-
(62-
As we learned in the previous module, the aggregate consumption function shows the relationship between disposable income and consumer spending. Let’s continue to assume that the aggregate consumption function is of the same form as in Equation 61-
(62-
In our simplified model, we will also assume planned investment spending, IPlanned, is fixed.
We need one more concept before putting the model together: planned aggregate spending, the total amount of planned spending in the economy. Unlike firms, households don’t take unintended actions like unplanned inventory investment. So planned aggregate spending is equal to the sum of consumer spending and planned investment spending. We denote planned aggregate spending by AEPlanned, so:
Planned aggregate spending is the total amount of planned spending in the economy.
(62-
The level of planned aggregate spending in a given year depends on the level of real GDP in that year. To see why, let’s look at a specific example, shown in Table 62-1. We assume that the aggregate consumption function is:
(62-
62-1
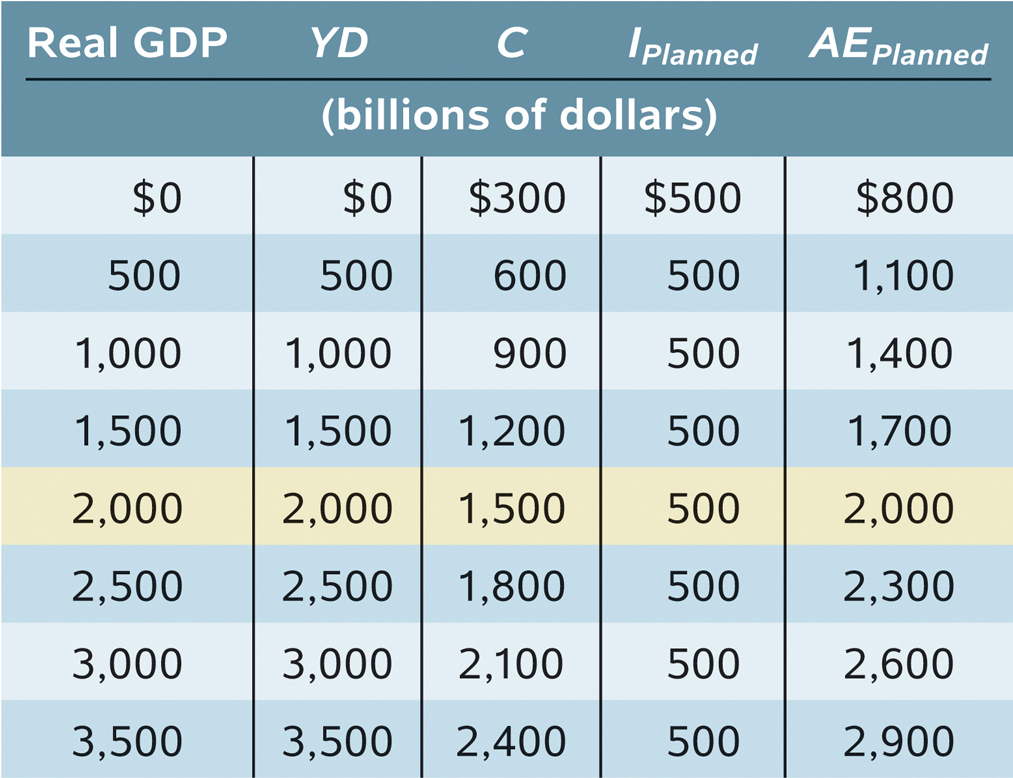
Real GDP, YD, C, IPlanned, and AEPlanned are all measured in billions of dollars, and we assume that the level of planned investment, IPlanned, is fixed at $500 billion per year. The first column shows possible levels of real GDP. The second column shows disposable income, YD, which in our simplified model is equal to real GDP. The third column shows consumer spending, C, equal to $300 billion plus 0.6 times disposable income, YD. The fourth column shows planned investment spending, IPlanned, which we have assumed is $500 billion regardless of the level of real GDP.
Finally, the last column shows planned aggregate spending, AEPlanned, the sum of aggregate consumer spending, C, and planned investment spending, IPlanned. (To economize on notation, we’ll assume that it is understood from now on that all the variables in Table 62-1 are measured in billions of dollars per year.) As you can see, a higher level of real GDP leads to a higher level of disposable income: every 500 increase in real GDP raises YD by 500, which in turn raises C by 500 × 0.6 = 300 and AEPlanned by 300.
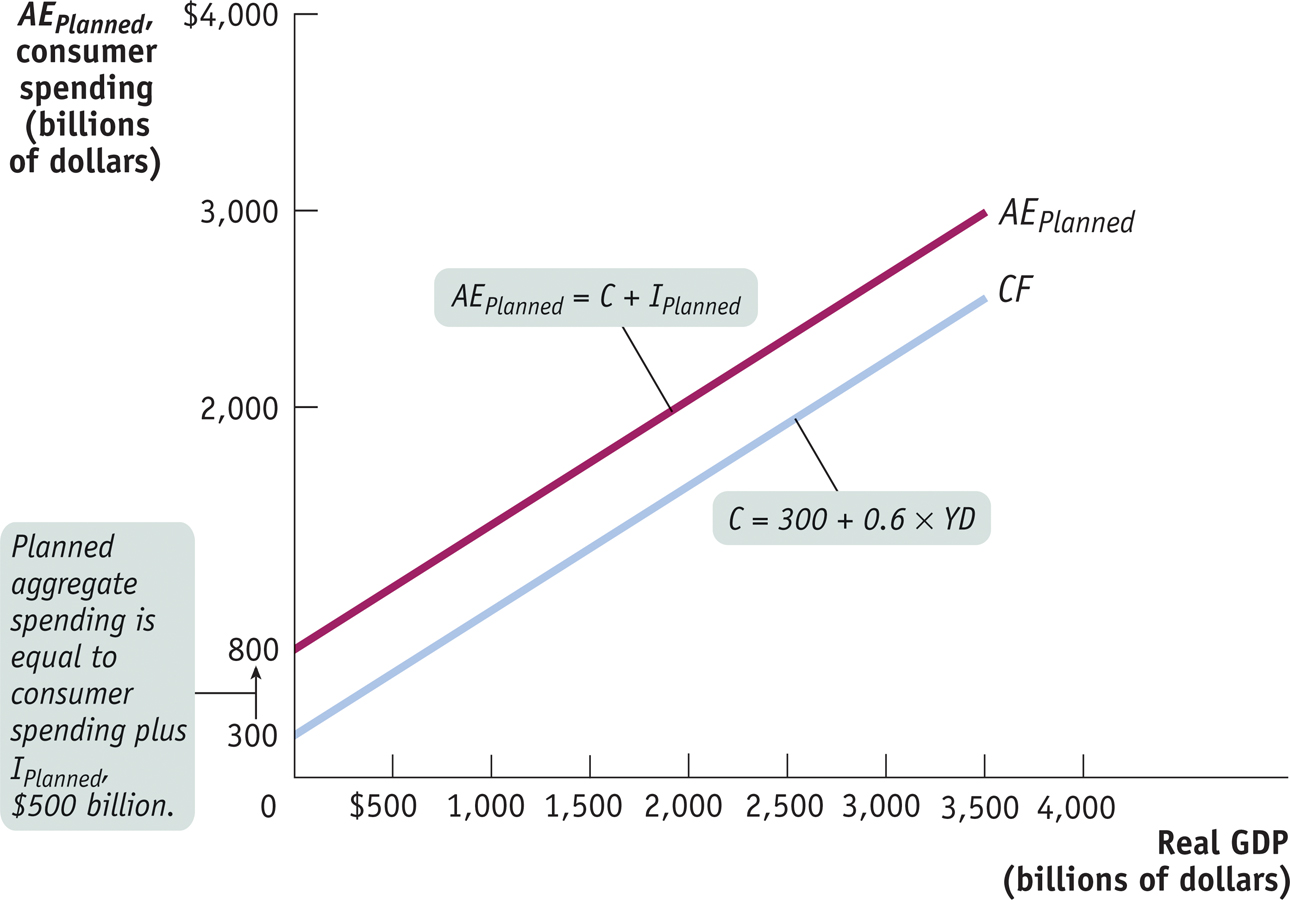
Figure 62-1 illustrates the information in Table 62-1 graphically. Real GDP is measured on the horizontal axis. CF is the aggregate consumption function; it shows how consumer spending depends on real GDP. AEPlanned, the planned aggregate spending line, corresponds to the aggregate consumption function shifted up by 500 (the amount of IPlanned). It shows how planned aggregate spending depends on real GDP. Both lines have a slope of 0.6, equal to MPC, the marginal propensity to consume.
But this isn’t the end of the story. Table 62-1 reveals that real GDP equals planned aggregate spending, AEPlanned, only when the level of real GDP is at 2,000. Real GDP does not equal AEPlanned at any other level. Is that possible? Didn’t we learn from the circular-
Income–Expenditure Equilibrium
For all but one value of real GDP shown in Table 62-1, real GDP is either more or less than AEPlanned, the sum of consumer spending and planned investment spending. For example, when real GDP is 1,000, consumer spending, C, is 900 and planned investment spending is 500, making planned aggregate spending 1,400. This is 400 more than the corresponding level of real GDP. Now consider what happens when real GDP is 2,500; consumer spending, C, is 1,800 and planned investment spending is 500, making planned aggregate spending only 2,300, 200 less than real GDP.
62-2
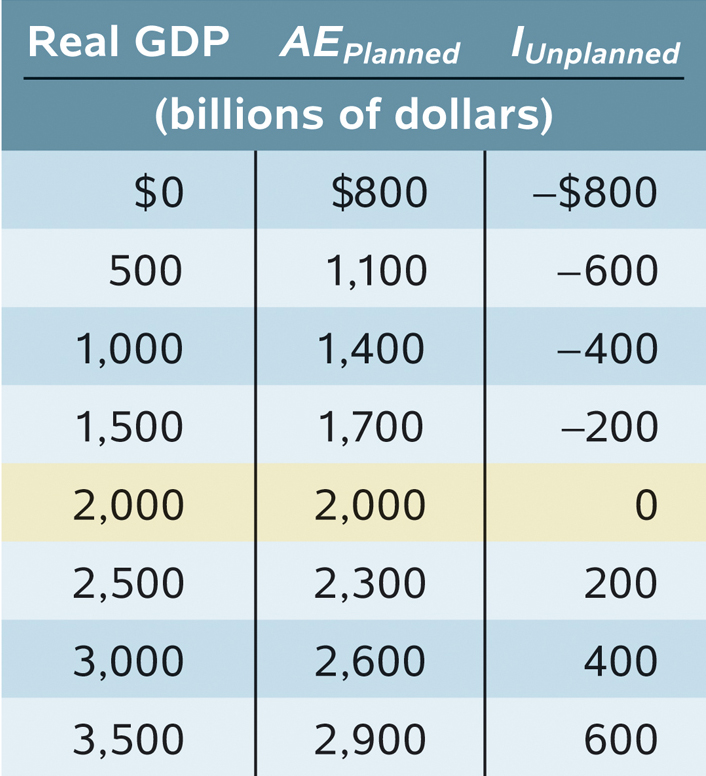
As we’ve just explained, planned aggregate spending can be different from real GDP only if there is unplanned inventory investment, IUnplanned, in the economy. Let’s examine Table 62-2, which includes the numbers for real GDP and for planned aggregate spending from Table 62-1. It also includes the levels of unplanned inventory investment, IUnplanned, that each combination of real GDP and planned aggregate spending implies. For example, if real GDP is 2,500, planned aggregate spending is only 2,300. This 200 excess of real GDP over AEPlanned must consist of positive unplanned inventory investment. This can happen only if firms have overestimated sales and produced too much, leading to unintended additions to inventories. More generally, any level of real GDP in excess of 2,000 corresponds to a situation in which firms are producing more than consumers and other firms want to purchase, creating an unintended increase in inventories.
Conversely, a level of real GDP below 2,000 implies that planned aggregate spending is greater than real GDP. For example, when real GDP is 1,000, planned aggregate spending is much larger, at 1,400. The 400 excess of AEPlanned over real GDP corresponds to negative unplanned inventory investment equal to −400. More generally, any level of real GDP below 2,000 implies that firms have underestimated sales, leading to a negative level of unplanned inventory investment in the economy.
By putting together Equations 62-
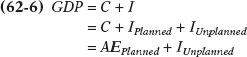
So whenever real GDP exceeds AEPlanned, IUnplanned is positive; whenever real GDP is less than AEPlanned, IUnplanned is negative.

But firms will act to correct their mistakes. We’ve assumed that they don’t change their prices, but they can adjust their output. Specifically, they will reduce production if they have experienced an unintended rise in inventories or increase production if they have experienced an unintended fall in inventories. And these responses will eventually eliminate the unanticipated changes in inventories and move the economy to a point at which real GDP is equal to planned aggregate spending.
Staying with our example, if real GDP is 1,000, negative unplanned inventory investment will lead firms to increase production, leading to a rise in real GDP. In fact, this will happen whenever real GDP is less than 2,000—
The economy is in income–
Income–
The only situation in which firms won’t have an incentive to change output in the next period is when aggregate output, measured by real GDP, is equal to planned aggregate spending in the current period, an outcome known as income–
Figure 62-2 illustrates the concept of income–
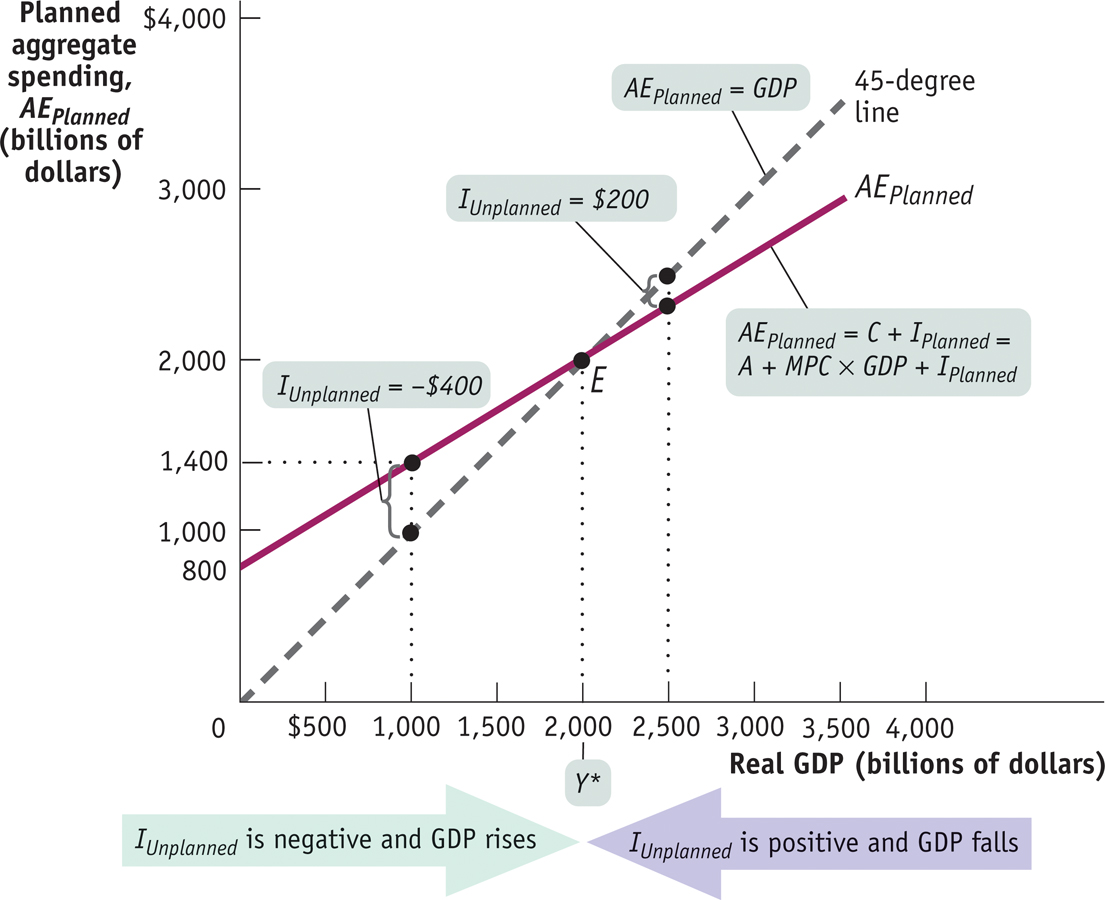
The dashed line, which goes through the origin with a slope of 1 (often called a 45-
Now consider what happens if the economy isn’t in income–
The Keynesian cross diagram identifies income–
The type of diagram shown in Figure 62-2, which identifies income–
The Multiplier Process and Inventory Adjustment
We’ve just learned about a very important feature of the macroeconomy: when planned spending by households and firms does not equal the current aggregate output by firms, this difference shows up in changes in inventories. The response of firms to those inventory changes moves real GDP over time to the point at which real GDP and planned aggregate spending are equal. That’s why, as we mentioned earlier, changes in inventories are considered a leading indicator of future economic activity.
Now that we understand how real GDP moves to achieve income–
In our simple model there are only two possible sources of a shift of the planned aggregate spending line: a change in planned investment spending, IPlanned, or a shift of the aggregate consumption function, CF. For example, a change in IPlanned can occur because of a change in the interest rate. (Remember, we’re assuming that the interest rate is fixed by factors that are outside the model. But we can still ask what happens when the interest rate changes.) A shift of the aggregate consumption function (that is, a change in its vertical intercept, A) can occur because of a change in aggregate wealth—
62-3
When the planned aggregate spending line shifts—
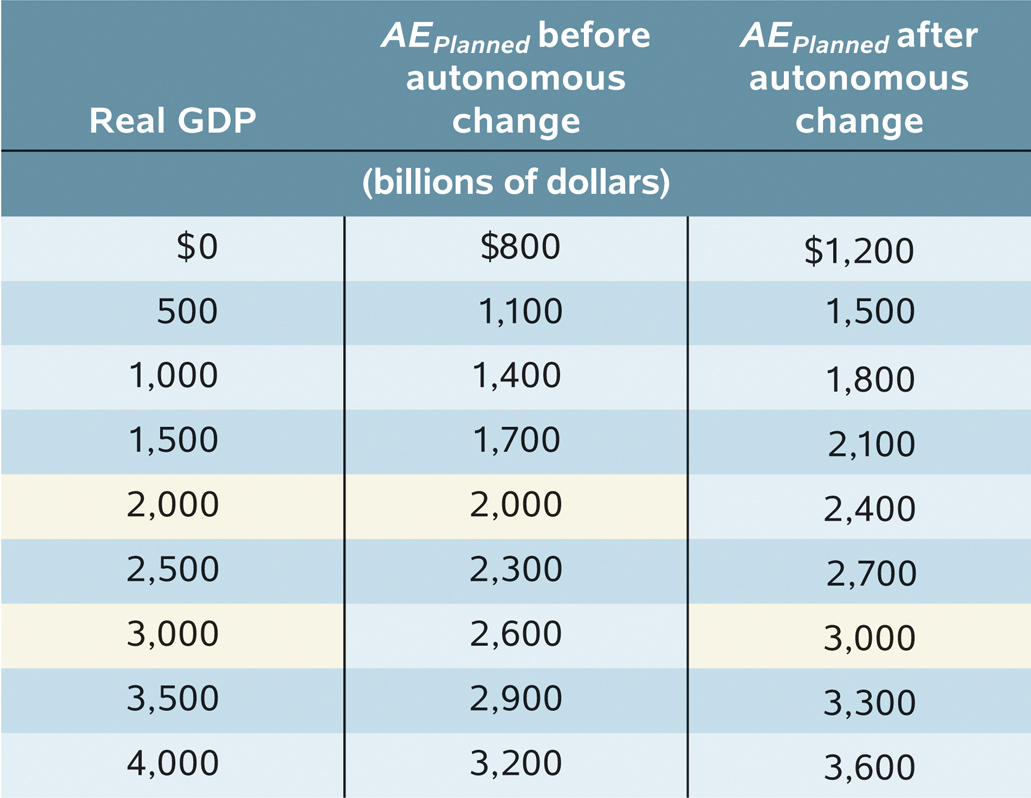
Table 62-3 and Figure 62-3 start from the same numerical example we used in Table 62-2 and Figure 62-2. They also show the effect of an autonomous increase in planned aggregate spending of 400—
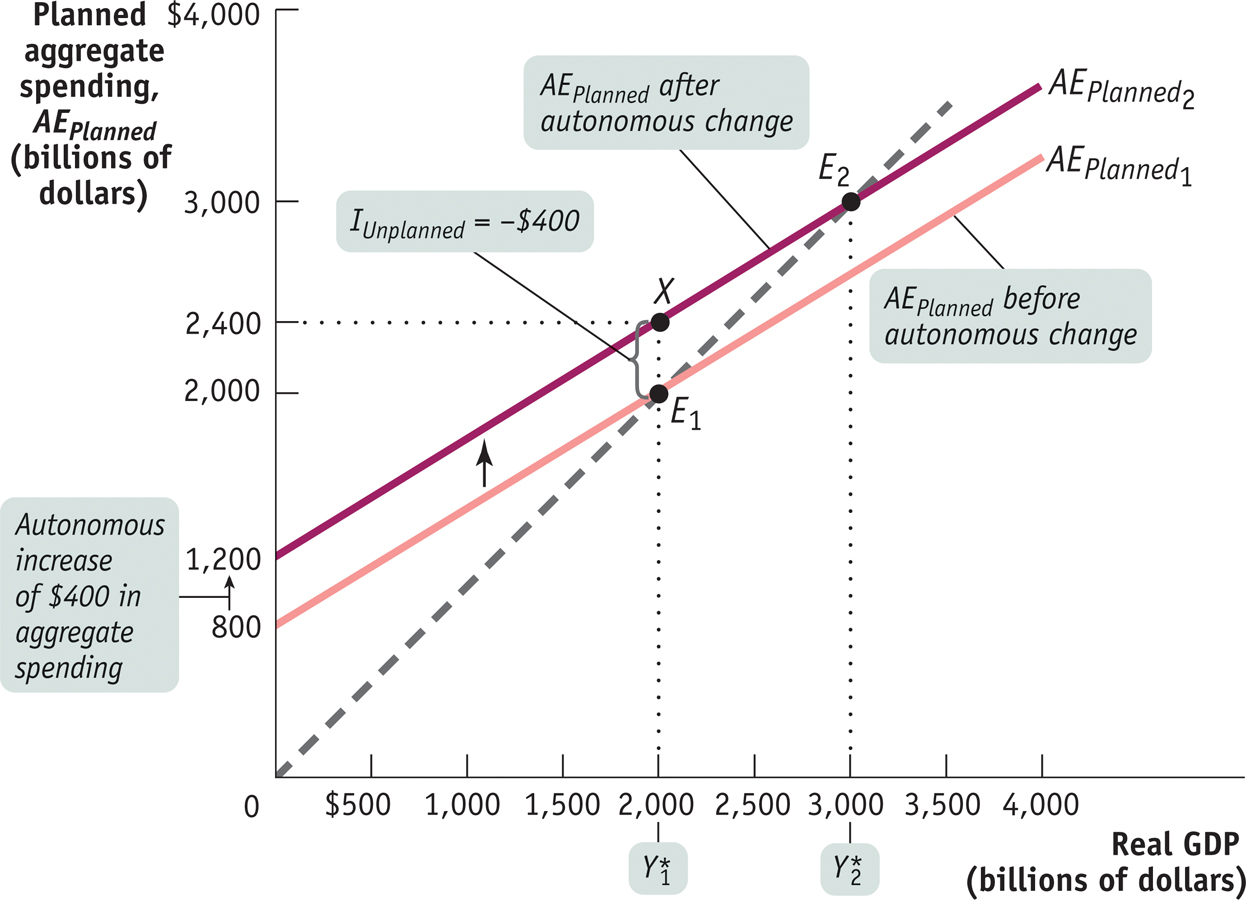
 , equal to 2,000. An autonomous increase in AEPlanned of 400 shifts the planned aggregate spending line upward by 400. The economy is no longer in income–
, equal to 2,000. An autonomous increase in AEPlanned of 400 shifts the planned aggregate spending line upward by 400. The economy is no longer in income–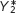 , equal to 3,000.
, equal to 3,000.The same result is visible in Figure 62-3. The initial income–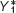 is 2,000. The autonomous rise in planned aggregate spending shifts the planned aggregate spending line up, leading to a new income–
is 2,000. The autonomous rise in planned aggregate spending shifts the planned aggregate spending line up, leading to a new income–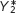 is 3,000.
is 3,000.
The fact that the rise in income–
We can examine in detail what underlies the multistage multiplier process by looking more closely at Figure 62-3. First, starting from E1, the autonomous increase in planned aggregate spending leads to a gap between planned aggregate spending and real GDP. This is represented by the vertical distance between X, at 2,400, and E1, at 2,000. This gap illustrates an unplanned fall in inventory investment: IUnplanned = −400. Firms respond by increasing production, leading to a rise in real GDP from 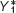 . The rise in real GDP translates into an increase in disposable income, YD.
. The rise in real GDP translates into an increase in disposable income, YD.
That’s the first stage in the chain reaction. But it doesn’t stop there—
We can summarize these results in an equation, where ΔAAEPlanned represents the autonomous change in AEPlanned, and 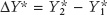 , the subsequent change in income–
, the subsequent change in income–
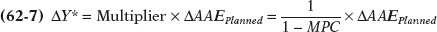
Recalling that the multiplier, 1/(1 − MPC), is greater than 1, Equation 62-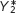 .
.
The Paradox of ThriftLet’s now consider what happens when there is a slump in consumer spending or investment spending, or both. This causes a fall in income–
In the paradox of thrift, households and firms cut their spending in anticipation of future tough economic times. These actions depress the economy, leaving households and firms worse off than if they hadn’t acted virtuously to prepare for tough times. It is called a paradox because what’s usually “good” (saving for hard times) is “bad” (because it can make everyone worse off).
We’ve seen that declines in planned investment spending are usually the major factor causing recessions, because historically they have been the most common source of autonomous reductions in aggregate spending. Likewise, we know that consumption spending can change as a result of an increase or decrease in the aggregate wealth or expected future disposable income of individuals. But regardless of the source, there are multiplier effects in the economy that magnify the size of the initial change in aggregate spending.
INVENTORIES AND THE END OF A RECESSION
A very clear example of the role of inventories in the multiplier process took place in late 2001, as that year’s recession came to an end.
The driving force behind the recession was a slump in business investment spending. It took several years before investment spending bounced back in the form of a housing boom. Still, the economy did start to recover in late 2001, largely because of an increase in consumer spending—
Initially, this increase in consumer spending caught manufacturers by surprise. Figure 62-4 shows changes in real GDP, real consumer spending, and real inventories in each quarter of 2001 and 2002. Notice the surge in consumer spending in the fourth quarter of 2001. It didn’t lead to a lot of GDP growth because it was offset by a plunge in inventories. But in the first quarter of 2002 producers greatly increased their production, leading to a jump in real GDP.
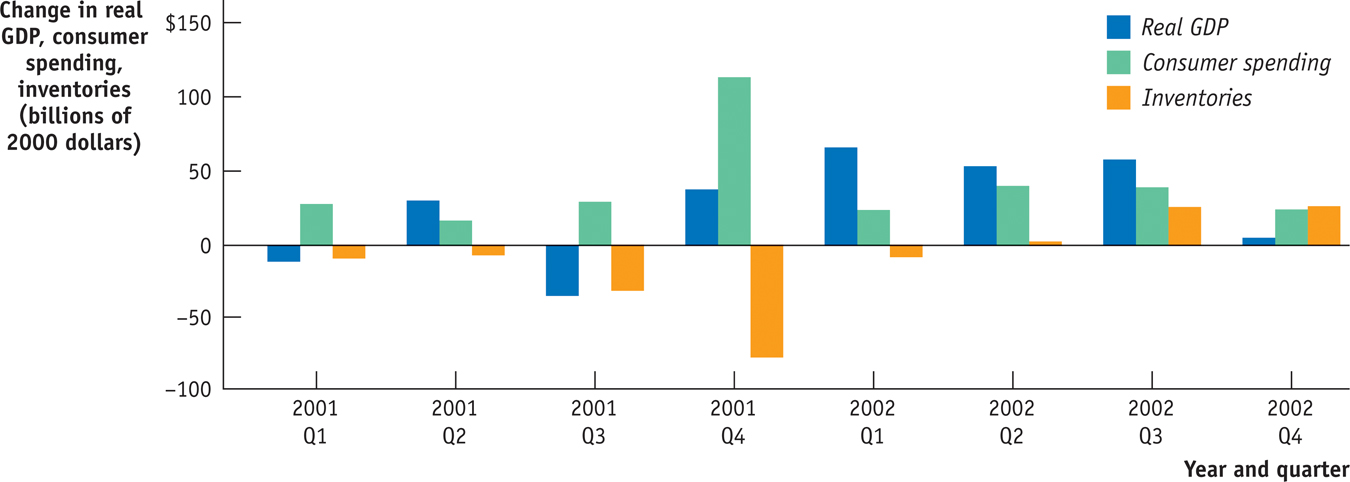
62
Solutions appear at the back of the book.
Check Your Understanding
Although economists believe that recessions typically begin as slumps in investment spending, they also believe that consumer spending eventually slumps during a recession. Explain why.
A slump in planned investment spending will lead to a fall in real GDP in response to an unanticipated increase in inventories. The fall in real GDP will translate into a fall in households’ disposable income, and households will respond by reducing consumer spending. The decrease in consumer spending leads producers to further decrease output, further lowering disposable income and leading to further reductions in consumer spending. So although the slump originated in investment spending, it will cause a reduction in consumer spending.-
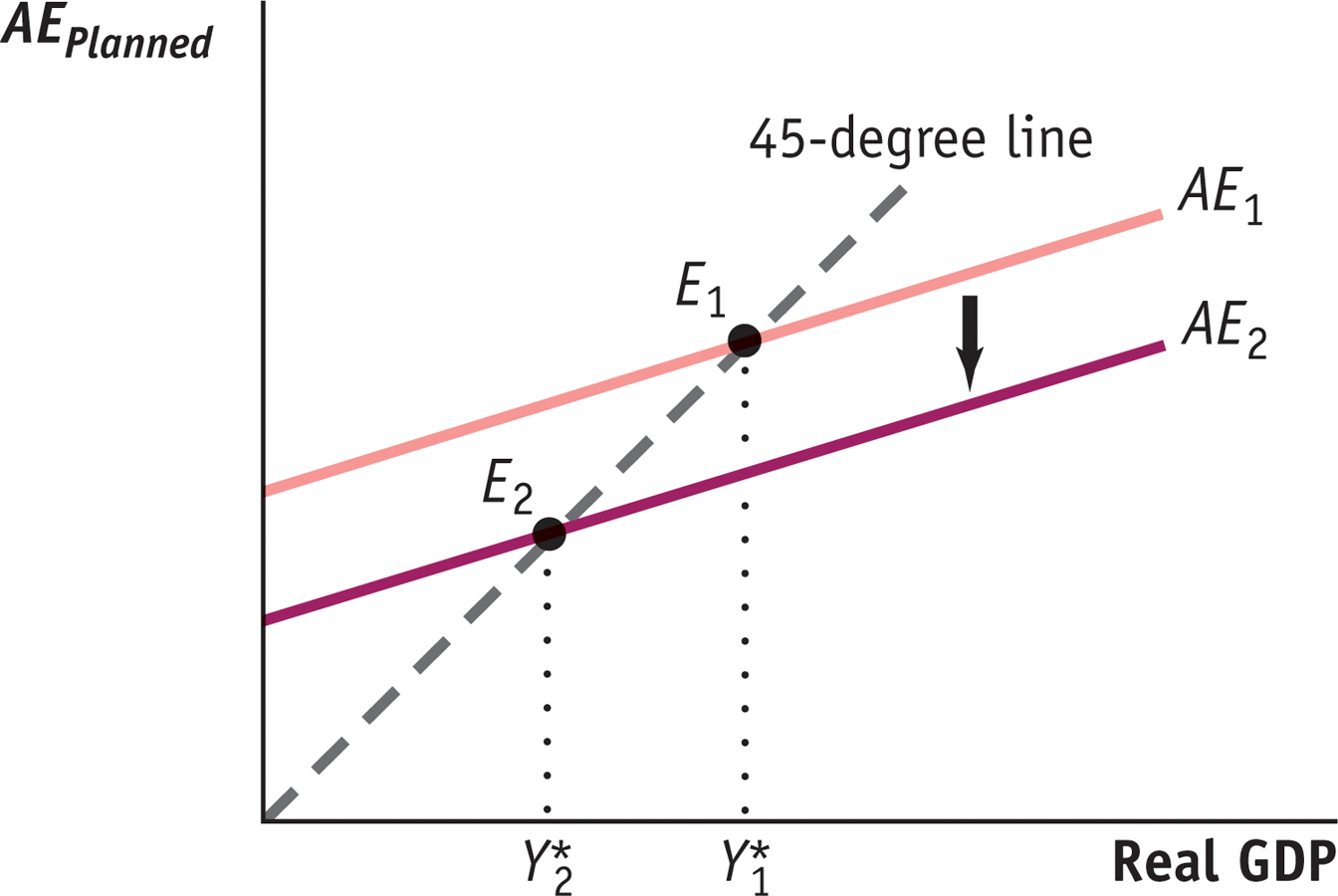
a. Use a diagram like Figure 62-3 to show what happens when there is an autonomous fall in planned aggregate spending. Describe how the economy adjusts to a new income–
expenditure equilibrium. After an autonomous fall in planned aggregate spending, the economy is no longer in equilibrium: real GDP is greater than planned aggregate spending. The accompanying figure shows this autonomous fall in planned aggregate spending by the shift of the aggregate spending curve from AE1 to AE2. The difference between the two results in positive unplanned inventory investment: there is an unanticipated increase in inventories. Firms will respond by reducing production. This will eventually move the economy to a new equilibrium. In the accompanying figure, this is illustrated by the movement from the initial income–expenditure equilibrium at E1 to the new income–expenditure equilibrium at E2. As the economy moves to its new equilibrium, real GDP falls from its initial income–expenditure equilibrium level at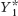 to its new lower level,
to its new lower level, 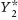 .
.
-
b. Suppose Y* is originally $500 billion, the autonomous reduction in planned aggregate spending is $300 million ($0.3 billion), and MPC = 0.5. Calculate Y* after such a change.
We know that the change in income–expenditure equilibrium GDP is given by Equation 62-7: ΔY* = Multiplier × ΔAAEPlanned. Here, the multiplier = 1/(1 − 0.5) = 1/0.5 = 2. So a $300 million autonomous reduction in planned aggregate spending will lead to a 2 × $300 million = $600 million ($0.6 billion) fall in income–expenditure equilibrium GDP. The new Y* will be $500 billion − $0.6 billion = $499.4 billion.
-
Multiple-
Question
The aggregate consumption function shows the relationship between
A. B. C. D. E. Question
In income–
expenditure equilibrium A. B. C. D. E. Question
Planned aggregate spending
A. B. C. D. E. Question
If real GDP is less than planned aggregate spending then
A. B. C. D. E. Question
Suppose there is a $200 million increase in autonomous planned aggregate spending. This will cause the planned aggregate spending line to shift upwards by __________ and real GDP will increase by ____________.
A. B. C. D. E.
Critical-
Question 1.1
What is the value of unplanned inventory investment in income–