1.2 21The Market for Loanable Funds

Shutterstock

The Role of the Loanable Funds Market

For the economy as a whole, savings always equals investment spending. In a closed economy, savings is equal to national savings. In an open economy, savings is equal to national savings plus capital inflow. At any given time, however, savers, the people with funds to lend, are usually not the same as borrowers, the people who want to borrow to finance their investment spending. How are savers and borrowers brought together?

Savers and borrowers are matched up with one another in much the same way producers and consumers are matched up: through markets governed by supply and demand. In Figure 10-2, the expanded circular-flow diagram, we noted that the financial markets channel the savings of households to businesses that want to borrow in order to purchase capital equipment. It’s now time to take a look at how those financial markets work.

Although there are a large number of different financial markets in the financial system, such as the bond market and the stock market, economists often work with a simplified model in which they assume that there is just one market. The market brings together those who want to lend money (savers) and those who want to borrow (firms with investment spending projects). This hypothetical market is known as the loanable funds market.

The price that is determined in the loanable funds market is the interest rate, denoted by r. As we’ve learned, loans typically specify a nominal interest rate. So although we call r “the interest rate,” it is with the understanding that r is a nominal interest rate—an interest rate that is unadjusted for inflation.

In the interest of simplicity we are also going to assume that there is only one type of loan. This, despite the fact that in reality there are many different kinds of interest rates because there are many different kinds of loans—short-term loans, long-term loans, loans made to corporate borrowers, loans made to governments, and so on.

Now we’re ready to analyze how savings and investment get matched up.

The Demand for Loanable Funds

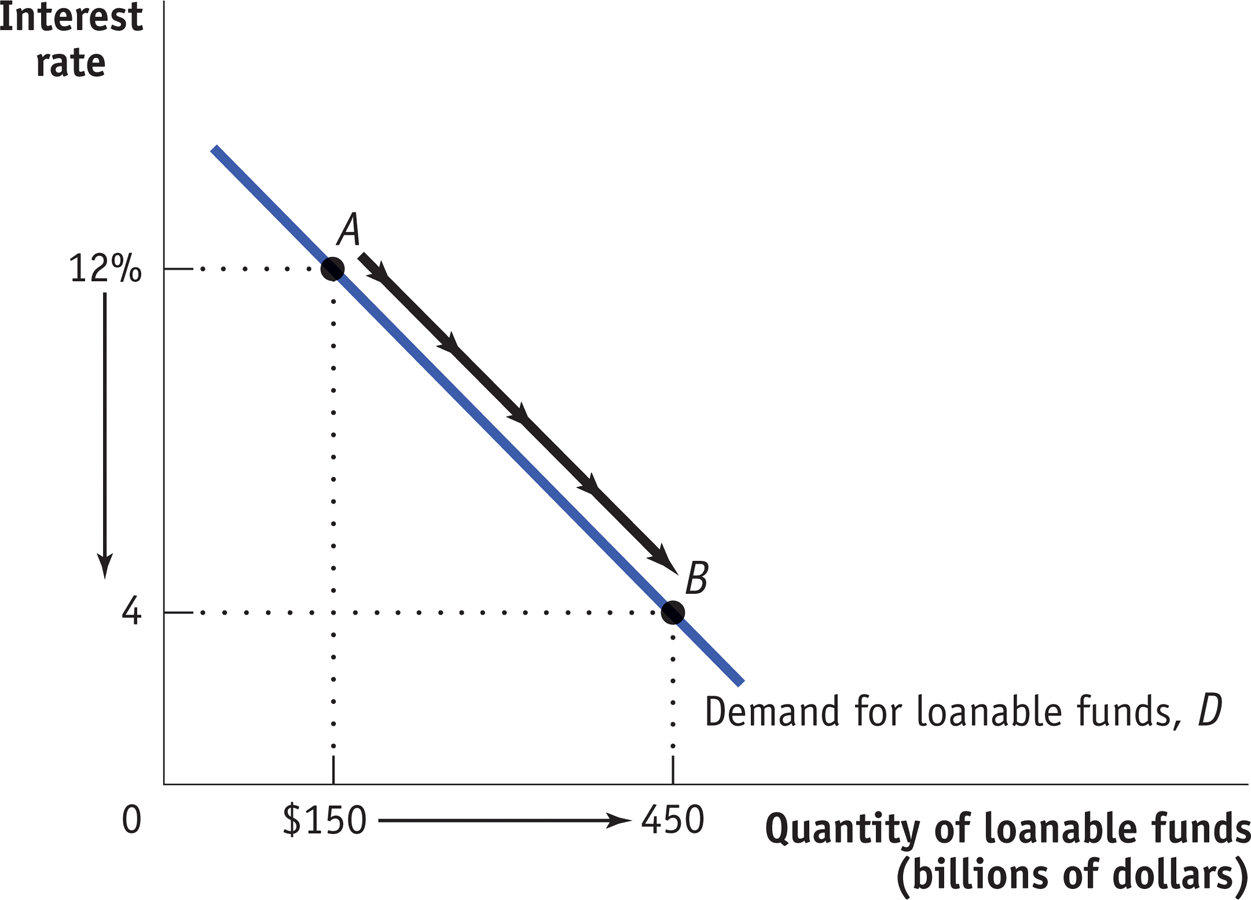
Figure 21-1 illustrates a hypothetical demand curve for loanable funds, D, which slopes downward. On the horizontal axis we show the quantity of loanable funds demanded. On the vertical axis we show the interest rate, which is the “price” of borrowing. But why does the demand curve for loanable funds slope downward?

The demand curve for loanable funds slopes downward: the lower the interest rate, the greater the quantity of loanable funds demanded. Here, reducing the interest rate from 12% to 4% increases the quantity of loanable funds demanded from $150 billion to $450 billion.

To answer this question, consider what a firm is doing when it engages in investment spending—say, by buying new equipment. Investment spending means laying out money right now, expecting that this outlay will lead to higher profits at some point in the future. In fact, however, the promise of a dollar five or ten years from now is worth less than an actual dollar right now.

When firms invest in projects, they spend money today in return for an expected payoff in the future.

Bob Thomason/Getty Images

So an investment is worth making only if it generates a future return that is greater than the monetary cost of making the investment today. How much greater? To answer that, we need to take into account the present value of the future return the firm expects to get.

We will look at the concept of present value in more detail in the next module. For now, keep in mind that in present value calculations, we use the interest rate to determine how the value of a dollar in the future compares to the value of a dollar today. But the fact is that future dollars are worth less than a dollar today, and they are worth even less when the interest rate is higher.

The intuition behind present value calculations is simple. The interest rate measures the opportunity cost of investment spending that results in a future return: instead of spending money on an investment spending project, a company could simply put the money into the bank and earn interest on it. And the higher the interest rate, the more attractive it is to simply put money into the bank instead of investing it in an investment spending project. In other words, the higher the interest rate, the higher the opportunity cost of investment spending. And, the higher the opportunity cost of investment spending, the lower the number of investment spending projects firms want to carry out, and therefore the lower the quantity of loanable funds demanded. It is this insight that explains why the demand curve for loanable funds is downward sloping.

When businesses engage in investment spending, they spend money right now in return for an expected payoff in the future. So, to evaluate whether a particular investment spending project is worth undertaking, a business must compare the present value of the future payoff with the current cost of that project. If the present value of the future payoff is greater than the current cost, a project is profitable and worth investing in. If the interest rate falls, then the present value of any given project rises, so more projects pass that test. If the interest rate rises, then the present value of any given project falls, so fewer projects pass that test.

So total investment spending, and therefore the demand for loanable funds to finance that spending, is negatively related to the interest rate. Thus, the demand curve for loanable funds slopes downward. You can see this in Figure 21-1. When the interest rate falls from 12% to 4%, the quantity of loanable funds demanded rises from $150 billion (point A) to $450 billion (point B).

The Supply of Loanable Funds

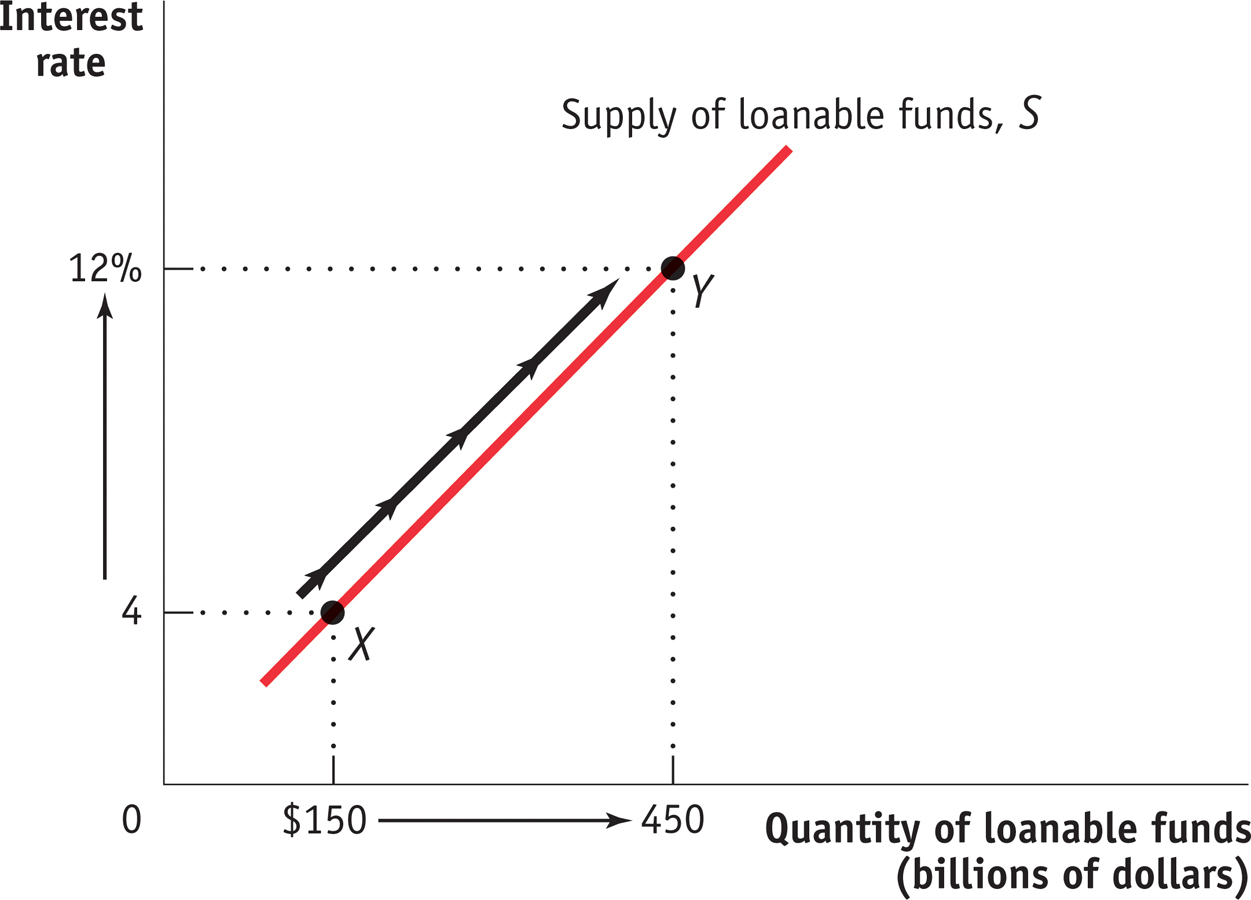
Figure 21-2 shows a hypothetical supply curve for loanable funds, S. Again, the interest rate plays the same role that the price plays in ordinary supply and demand analysis. But why is this curve upward sloping?

The supply curve for loanable funds slopes upward: the higher the interest rate, the greater the quantity of loanable funds supplied. Here, increasing the interest rate from 4% to 12% increases the quantity of loanable funds supplied from $150 billion to $450 billion.

Savers supply loanable funds to businesses and incur an opportunity cost in doing so.

Hemera/Thinkstock

The answer is that loanable funds are supplied by savers, and savers incur an opportunity cost when they lend to a business: the funds could instead be spent on consumption—say, a nice vacation. Whether a given saver becomes a lender by making funds available to borrowers depends on the interest rate received in return. By saving your money today and earning interest on it, you are rewarded with higher consumption in the future when the loan you made is repaid with interest.

So it is a good assumption that more people will forgo current consumption and make a loan to a borrower when the interest rate is higher. As a result, our hypothetical supply curve of loanable funds slopes upward. In Figure 21-2, lenders will supply $150 billion to the loanable funds market at an interest rate of 4% (point X); if the interest rate rises to 12%, the quantity of loanable funds supplied will rise to $450 billion (point Y).

The Equilibrium Interest Rate

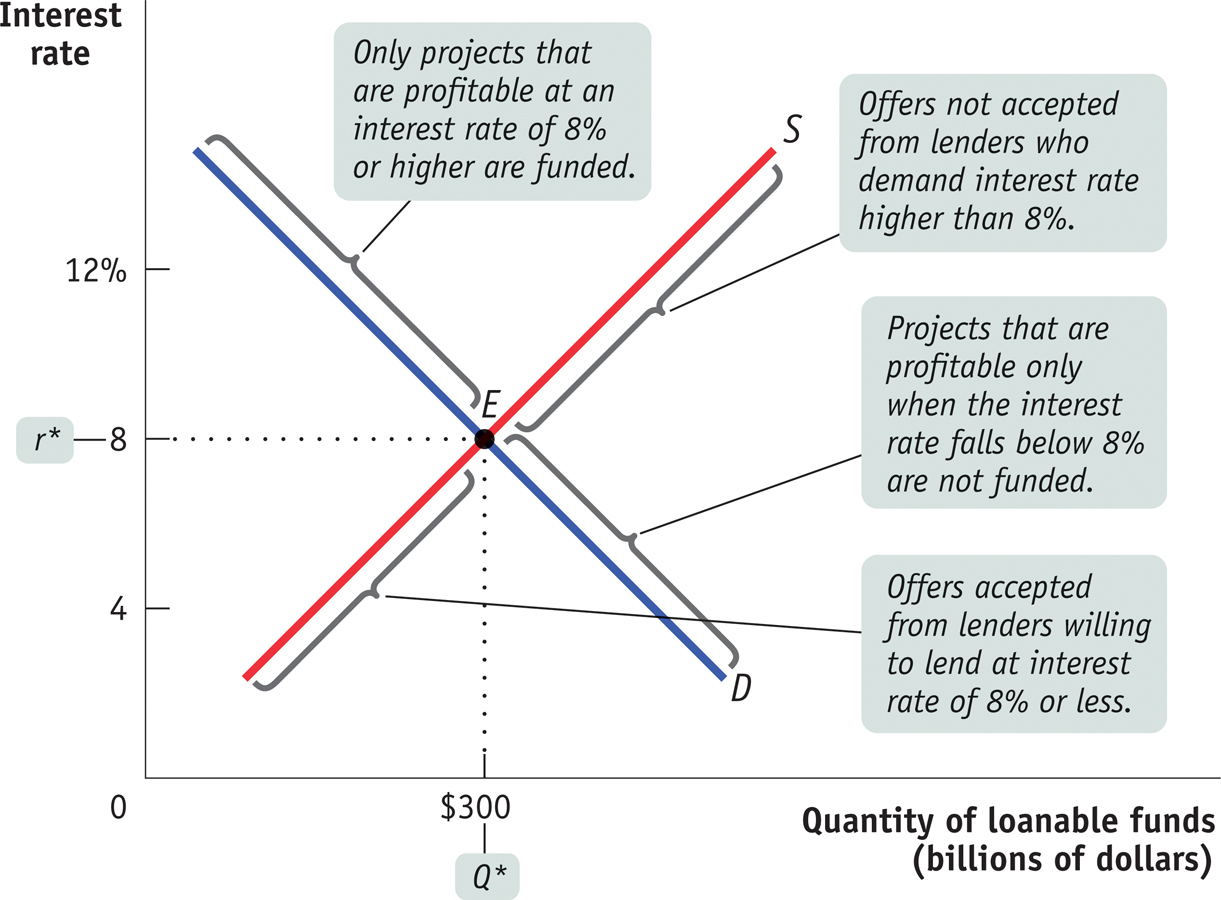
The interest rate at which the quantity of loanable funds supplied equals the quantity of loanable funds demanded is the equilibrium interest rate. As you can see in Figure 21-3, the equilibrium interest rate, r^*, and the total quantity of lending, Q^*, are determined by the intersection of the supply and demand curves, at point E. Here, the equilibrium interest rate is 8%, at which $300 billion is lent and borrowed. In this equilibrium, only investment spending projects that are profitable if the interest rate is 8% or higher are funded.

Projects that are profitable only when the interest rate falls below 8% are not funded. Correspondingly, only lenders who are willing to accept an interest rate of 8% or less will have their offers to lend funds accepted; lenders who demand an interest rate higher than 8% do not have their offers to lend accepted.

Figure 21-3 shows how the market for loanable funds matches up desired savings with desired investment spending: in equilibrium, the quantity of funds that savers want to lend is equal to the quantity of funds that firms want to borrow. The figure also shows that this match-up is efficient, in two senses. First, the right investments get made: the investment spending projects that are actually financed have higher payoffs (in terms of present value) than those that do not get financed. Second, the right people do the saving and lending: the savers who actually lend funds are willing to lend for lower interest rates than those who do not.

At the equilibrium interest rate, the quantity of loanable funds supplied equals the quantity of loanable funds demanded. Here, the equilibrium interest rate is 8%, with $300 billion of funds lent and borrowed. Lenders who demand an interest rate of 8% or lower have their offers of loans accepted; those who demand a higher interest rate do not. Projects that are profitable at an interest rate of 8% or higher are funded; those that are profitable only when the interest rate falls below 8% are not.

The insight that the loanable funds market leads to an efficient use of savings, although drawn from a highly simplified model, has important implications for real life: it is the reason that a well-functioning financial system increases an economy’s long-run economic growth rate.

Let’s look at how the market for loanable funds responds to shifts of demand and supply. As in the standard model of supply and demand, where the equilibrium price changes in response to shifts of the demand or supply curves, here the equilibrium interest rate changes when there are shifts of the demand curve for loanable funds, the supply curve for loanable funds, or both.

Shifts of the Demand for Loanable Funds

Let’s start by looking at the causes and effects of changes in demand.

The factors that can cause the demand curve for loanable funds to shift include the following:

1. Changes in perceived business opportunities. A change in beliefs about the payoff of investment spending can increase or reduce the amount of desired spending at any given interest rate. If there is great excitement over the business possibilities created by new technology, as there was when the Internet came into wide use in the 1990s, businesses will rush to buy computer equipment, put fiber-optic cables in the ground, and so on, shifting the demand for loanable funds to the right. But if there is disillusionment with technology-related investment, as there was in 2001 when many dot-com businesses failed, the demand for loanable funds will shift back to the left.
2. Changes in government borrowing. A government runs a budget deficit when, in a given year, it spends more than it receives. Running budget deficits can be a major source of demand for loanable funds, with the result that changes in the government budget deficit can shift the demand curve for loanable funds. For example, between 2000 and 2003, as the U.S. federal government went from a budget surplus to a budget deficit, the government went from being a net saver that provided loanable funds to the market to being a net borrower, borrowing funds from the market. In 2000, net federal borrowing was minus $189 billion, as the federal government was paying off some of its pre-existing debt. But by 2003, net federal borrowing was plus $416 billion because the government had to borrow large sums to pay its bills. This change had the effect, other things equal, of shifting the demand curve for loanable funds to the right.

Figure 21-4 shows the effects of an increase in the demand for loanable funds. S is the supply of loanable funds, and D₁ is the initial demand curve. The initial equilibrium interest rate is r₁. An increase in the demand for loanable funds means that the quantity of funds demanded rises at any given interest rate, so the demand curve shifts rightward to D₂. As a result, the equilibrium interest rate rises to r₂.

If the quantity of funds demanded by borrowers rises at any given interest rate, the demand for loanable funds shifts rightward from D₁ to D₂. As a result, the equilibrium interest rate rises from r₁ to r₂.

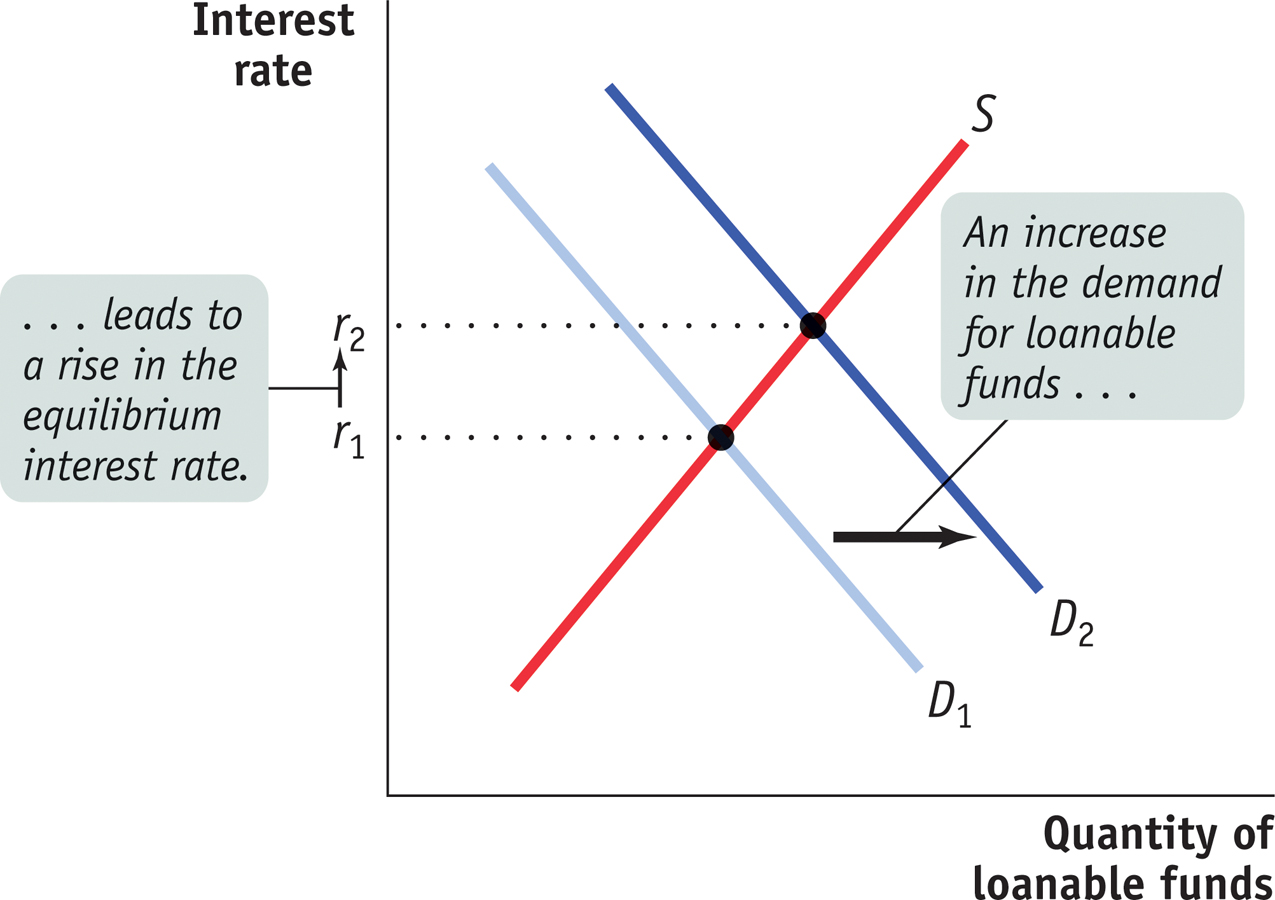
The fact that an increase in the demand for loanable funds leads, other things equal, to a rise in the interest rate has one especially important implication: it tells us that increasing or persistent government budget deficits are cause for concern because an increase in the government’s deficit shifts the demand curve for loanable funds to the right, which leads to a higher interest rate. If the interest rate rises, businesses will cut back on their investment spending.

So, other things equal, a rise in the government budget deficit tends to reduce overall investment spending. Economists call the negative effect of government budget deficits on investment spending crowding out. Concerns about crowding out are one key reason to worry about increasing or persistent budget deficits.

However, it’s important to add a qualification here: crowding out may not occur if the economy is depressed. When the economy is operating far below full employment, government spending can lead to higher incomes; and these higher incomes lead to increased savings at any given interest rate. Higher savings allows the government to borrow without raising interest rates. Many economists believe, for example, that the large budget deficits that the U.S. government ran from 2008 to 2013, in the face of a depressed economy, caused little if any crowding out.

Shifts of the Supply of Loanable Funds

Like the demand for loanable funds, the supply of loanable funds can shift. Among the factors that can cause the supply of loanable funds to shift are the following:

1. Changes in private savings behavior. A number of factors can cause the level of private savings to change at any given interest rate. For example, rising home prices in the United States will make many homeowners feel richer, leading them to spend more and save less. This will have the effect of shifting the supply curve of loanable funds to the left.
2. Changes in net capital inflows. Capital flows into and out of a country can change as investors’ perceptions of that country change. For example, Greece experienced large net capital inflows after the creation of the euro, Europe’s common currency, in 1999, because investors believed that Greece’s adoption of the euro as its currency had made it a safe place to put their funds. But, in the years that followed, worries about the Greek government’s solvency (and the discovery that it had been understating its debt) led to a collapse in investor confidence, and the net inflow of funds dried up. The effect of shrinking capital inflows was to shift the supply curve in the Greek loanable funds market to the left.

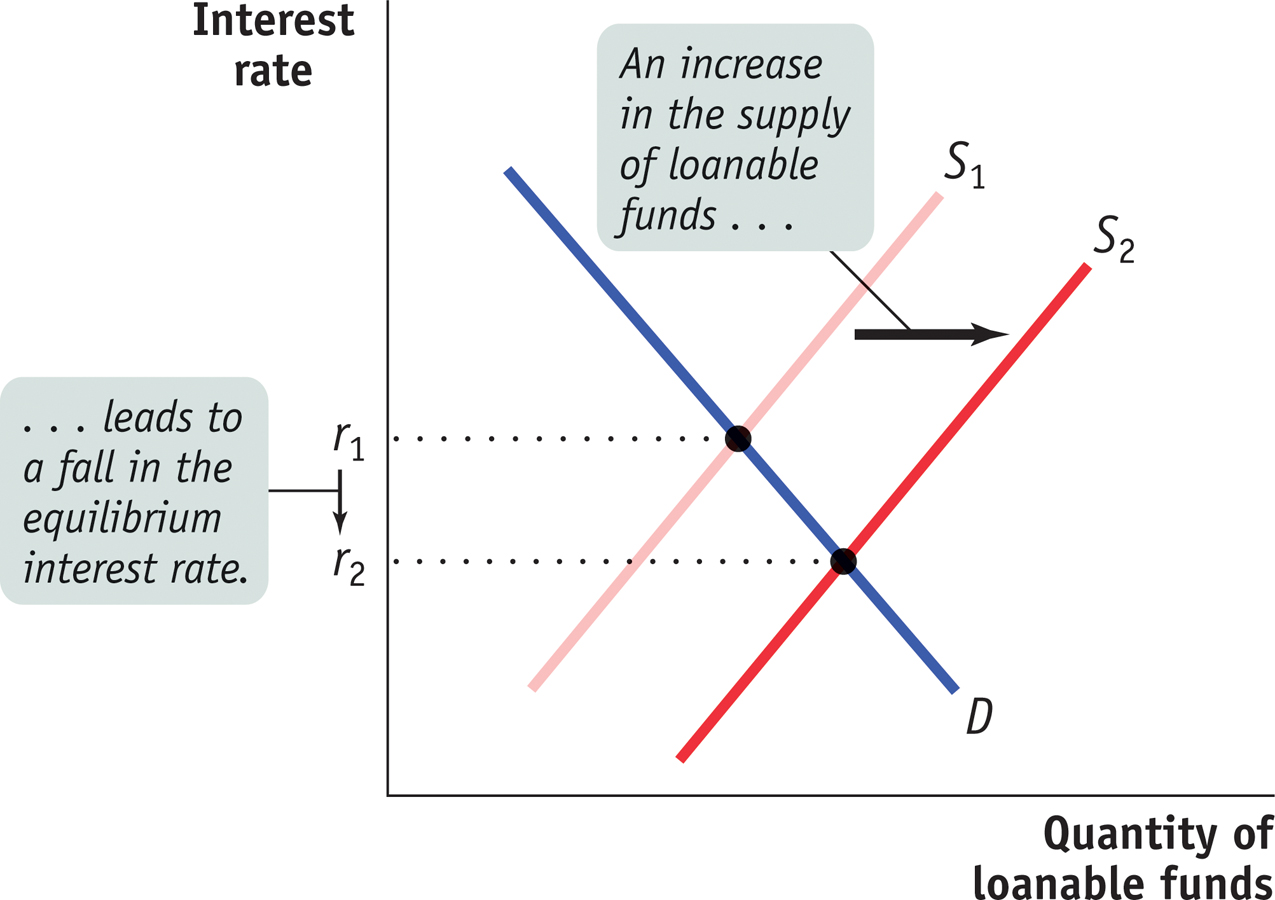
Figure 21-5 shows the effects of an increase in the supply of loanable funds. D is the demand for loanable funds, and S₁ is the initial supply curve. The initial equilibrium interest rate is r₁. An increase in the supply of loanable funds means that the quantity of funds supplied rises at any given interest rate, so the supply curve shifts rightward to S₂. As a result, the equilibrium interest rate falls to r₂.

If the quantity of funds supplied by lenders rises at any given interest rate, the supply of loanable funds shifts rightward from S₁ to S₂. As a result, the equilibrium interest rate falls from r₁ to r₂.

Inflation and Interest Rates

Anything that shifts either the supply of loanable funds curve or the demand for loanable funds curve changes the interest rate. Historically, major changes in interest rates have been driven by many factors, including changes in government policy and technological innovations that created new investment opportunities.

However, arguably the most important factor affecting interest rates over time—the reason, for example, that interest rates today are much lower than they were in the late 1970s and early 1980s—is changing expectations about future inflation, which shift both the supply and the demand for loanable funds.

To understand the effect of expected future inflation on interest rates, let’s look at an example: in the 1970s and 1980s higher than expected U.S. inflation reduced the real value of homeowners’ mortgages, which was good for the homeowners but bad for the banks. Economists summarize the effect of inflation on borrowers and lenders by distinguishing between the nominal interest rate and the real interest rate, where the difference is:

The true cost of borrowing is the real interest rate, not the nominal interest rate.

To see why, suppose a firm borrows $10,000 for one year at a 10% nominal interest rate. At the end of the year, it must repay $11,000—the amount borrowed plus the interest. But suppose that over the course of the year the average level of prices increases by 10%, so that the real interest rate is zero. Then the $11,000 repayment has the same purchasing power as the original $10,000 loan. In real terms, the borrower has received a zero-interest loan.

Similarly, the true payoff to lending is the real interest rate, not the nominal rate. Suppose that a bank makes a $10,000 loan for one year at a 10% nominal interest rate. At the end of the year, the bank receives an $11,000 repayment. But if the average level of prices rises by 10% per year, the purchasing power of the money the bank gets back is no more than that of the money it lent out. In real terms, the bank has made a zero-interest loan.

Now we can add an important detail to our analysis of the loanable funds market. Figures 21-4 and 21-5 are drawn with the vertical axis measuring the nominal interest rate for a given expected future inflation rate. Why do we use the nominal interest rate rather than the real interest rate? Because in the real world neither borrowers nor lenders know what the future inflation rate will be when they make a deal.

Actual loan contracts therefore specify a nominal interest rate rather than a real interest rate. Because we are holding the expected future inflation rate fixed in Figures 21-4 and 21-5, however, changes in the nominal interest rate also lead to changes in the real interest rate.

The expectations of borrowers and lenders about future inflation rates are normally based on recent experience. In the late 1970s, after a decade of high inflation, borrowers and lenders expected future inflation to be high. By the late 1990s, after a decade of fairly low inflation, borrowers and lenders expected future inflation to be low.

Changing expectations about future inflation is the most important factor affecting interest rates over time.

Shutterstock

These changing expectations about future inflation had a strong effect on the nominal interest rate, largely explaining why nominal interest rates were much lower in the early years of the twenty-first century than they were in the early 1980s. Let’s look at how changes in the expected future rate of inflation are reflected in the loanable funds model.

In Figure 21-6, the curves S₀ and D₀ show the supply and demand for loanable funds given that the expected future rate of inflation is 0%. In that case, equilibrium is at E₀ and the equilibrium nominal interest rate is 4%. Because expected future inflation is 0%, the equilibrium expected real interest rate over the life of the loan is also 4%.

D₀ and S₀ are the demand and supply curves for loanable funds when the expected future inflation rate is 0%. At an expected inflation rate of 0%, the equilibrium nominal interest rate is 4%. An increase in expected future inflation pushes both the demand and supply curves upward by 1 percentage point for every percentage point increase in expected future inflation. D₁₀ and S₁₀ are the demand and supply curves for loanable funds when the expected future inflation rate is 10%. The 10 percentage point increase in expected future inflation raises the equilibrium nominal interest rate to 14%. The expected real interest rate remains at 4%, and the equilibrium quantity of loanable funds also remains unchanged.

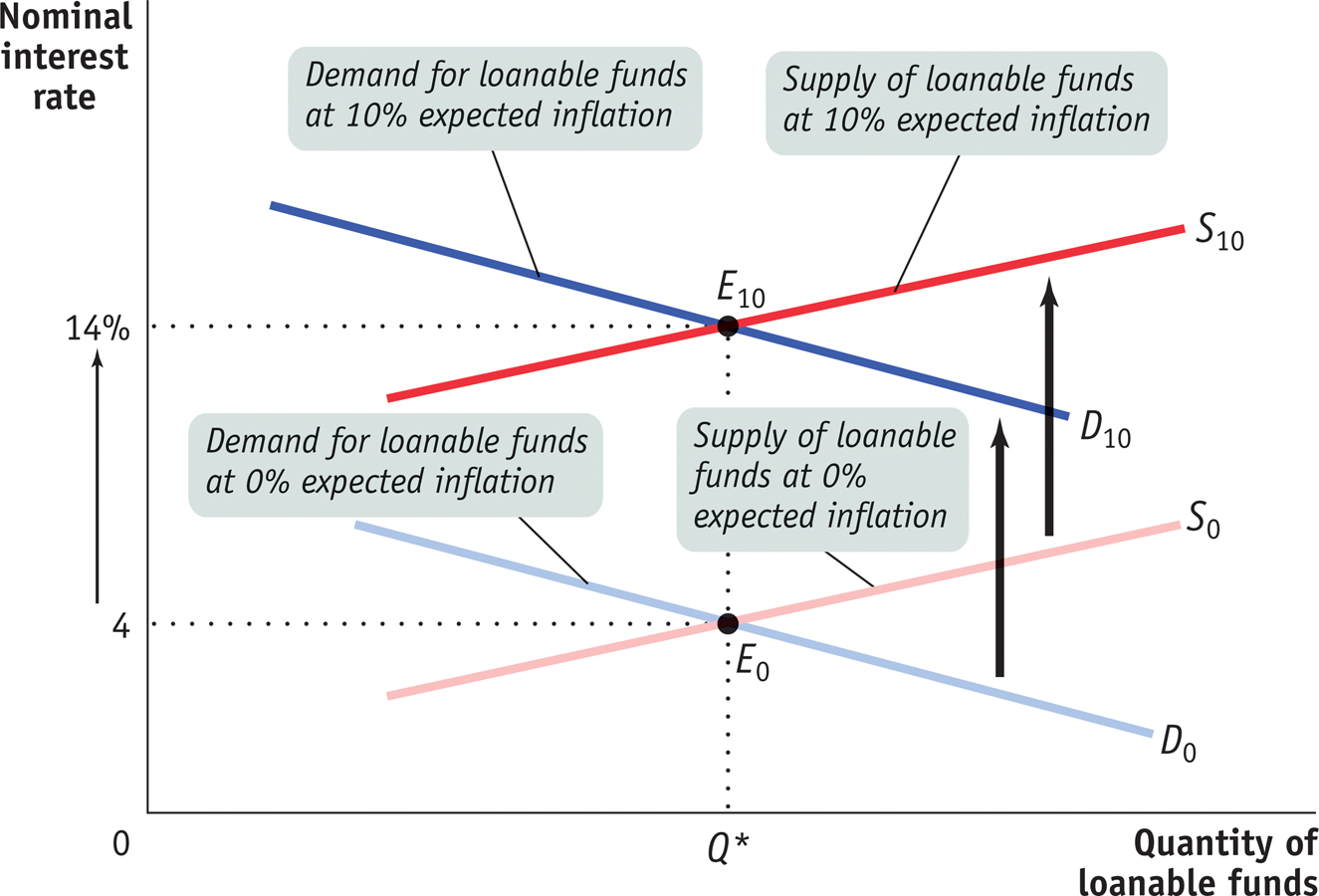
Now suppose that the expected future inflation rate rises to 10%. The demand curve for loanable funds shifts upward to D₁₀: borrowers are now willing to borrow as much at a nominal interest rate of 14% as they were previously willing to borrow at 4%. That’s because with a 10% inflation rate, a 14% nominal interest rate corresponds to a 4% real interest rate.

Similarly, the supply curve of loanable funds shifts upward to S₁₀: lenders require a nominal interest rate of 14% to persuade them to lend as much as they would previously have lent at 4%. The new equilibrium is at E₁₀: the result of an expected future inflation rate of 10% is that the equilibrium nominal interest rate rises from 4% to 14%.

This situation can be summarized as a general principle, known as the Fisher effect, which states that the expected real interest rate is unaffected by changes in expected future inflation. According to the Fisher effect, an increase in expected future inflation drives up the nominal interest rate, where each additional percentage point of expected future inflation drives up the nominal interest rate by 1 percentage point.

The central point is that both lenders and borrowers base their decisions on the expected real interest rate. As a result, a change in the expected rate of inflation does not affect the equilibrium quantity of loanable funds or the expected real interest rate; all it affects is the equilibrium nominal interest rate.

FIFTY YEARS OF FLUCTUATIONS IN U.S. INTEREST RATES

There have been some large movements in U.S. interest rates over the past half-century. These movements clearly show how both changes in expected future inflation and changes in the expected return on investment spending move interest rates.

Panel (a) of Figure 21-7 illustrates the first effect. It shows the average interest rate on bonds issued by the U.S. government—specifically, bonds for which the government promises to repay the full amount after 10 years—from 1960 to 2012, along with the rate of consumer price inflation over the same period. As you can see, the big story about interest rates is the way they soared in the 1970s, before coming back down in the 1980s.

FIGURE21-7Changes in U.S. Interest Rates Over Time

Sources: Federal Reserve Bank of St. Louis; Bureau of Labor Statistics.

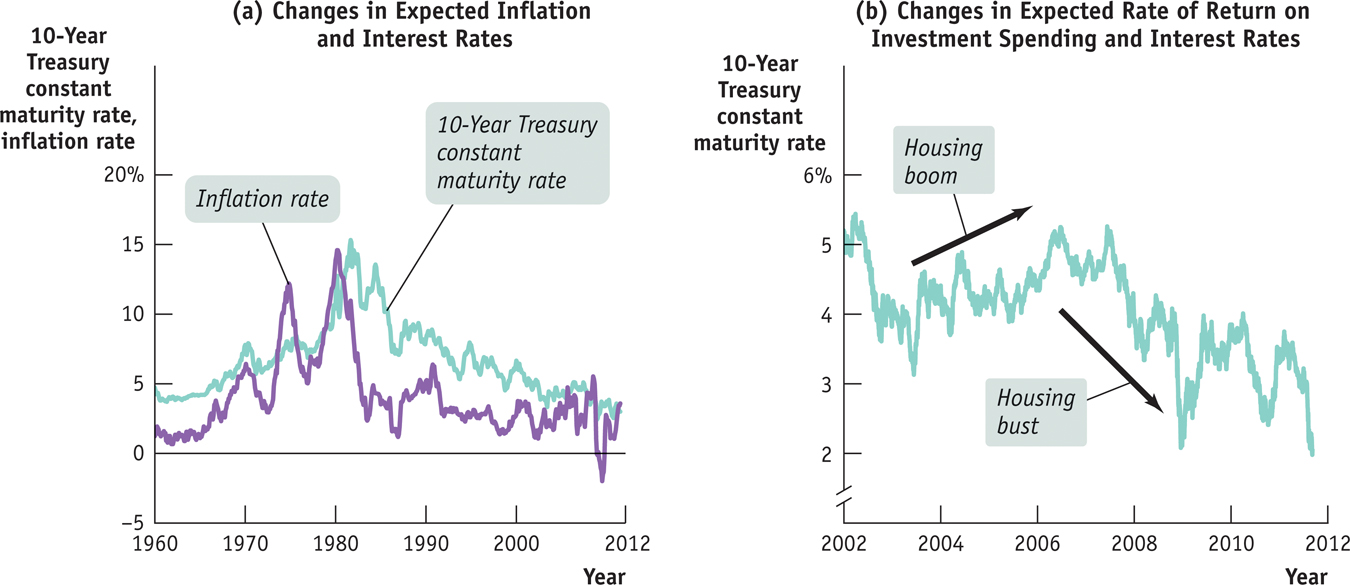
It’s not hard to see why that happened: inflation shot up during the 1970s, leading to widespread expectations that high inflation would continue. And as we’ve seen, expected inflation raises the equilibrium interest rate. As inflation came down in the 1980s, so did expectations of future inflation, and this brought interest rates down as well.

Panel (b) illustrates the second effect: changes in the expected return on investment spending and interest rates, with a “close-up” of interest rates from 2002 to 2012. Notice the rise in interest rates during the middle years of the last decade, followed by a sharp drop. We know from other evidence (such as surveys of investor opinion) that expected inflation didn’t change much over those years.

What happened, instead, was the boom and bust in housing: interest rates rose as demand for housing soared, pushing the demand curve for loanable funds to the right, then fell as the housing boom collapsed, shifting the demand curve for loanable funds back to the left. Throughout this whole process, total savings was equal to total investment spending, and the rise and fall of the interest rate played a key role in matching lenders with borrowers.

21

Check Your Understanding

Does each of the following affect either the supply or the demand for loanable funds, and if so, does the affected curve increase (shift to the right) or decrease (shift to the left)?