1.1 Module 43: The Cost-Minimizing Input Combination

(left) Beth Hail/Bloomberg via Getty Images;
(right) iStockphoto

In the previous section we discussed the markets for factors of production and how firms determine the optimal quantity of each factor to hire. But firms don’t determine how much of each input to hire separately. Production requires multiple inputs, and firms must decide what combination of inputs to use to produce their output. In this module, we will look at how firms decide the optimal combination of factors for producing the desired level of output.

Alternative Input Combinations

In many instances a firm can choose among a number of alternative combinations of inputs that will produce a given level of output. For example, on George and Martha’s wheat farm, the decision might involve labor and capital. To produce their optimal quantity of wheat, they could choose to have a relatively capital-intensive operation by investing in several tractors and other mechanized farm equipment and hiring relatively little labor. Alternatively, they could have a more labor-intensive operation by hiring a lot of workers to do much of the planting and harvesting by hand.

The same amount of wheat can be produced using many different combinations of capital and labor. George and Martha must determine which combination of inputs will maximize their profits.

To begin our study of the optimal combination of inputs, we’ll look at the relationship between the inputs used for production. Depending on the situation, inputs can be either substitutes or complements.

Substitutes and Complements in Factor Markets

Early in this book we discussed substitutes and complements in the context of the supply and demand model. Two goods are substitutes if a rise in the price of one good makes consumers more willing to buy the other good. For example, an increase in the price of oranges will cause some buyers to switch from purchasing oranges to purchasing tangerines.

ATMs can substitute for bank tellers.

iStockphoto

When buyers tend to consume two goods together, the goods are known as complements. For example, cereal and milk are considered complements because many people consume them together. If the price of cereal increases, people will buy less cereal and therefore need less milk. The decision about how much of a good to buy is influenced by the prices of related goods.

The concepts of substitutes and complements also apply to a firm’s purchase of inputs. And just as the price of related goods affects consumers’ purchasing decisions, the price of other inputs can affect a firm’s decision about how much of an input it will use. In some situations, capital and labor are substitutes. For example, George and Martha can produce the same amount of wheat by substituting more tractors for fewer farm workers. Likewise, ATM machines can substitute for bank tellers.

Capital and labor can also be complements when more of one increases the marginal product of the other. For example, a farm worker is more productive when George and Martha buy a tractor, and each tractor requires a worker to drive it. Office workers are more productive when they can use faster computers, and doctors are more productive with modern X-ray machines. In these cases the quantity and quality of capital available affect the marginal product of labor, and thus the demand for labor.

Given the relationship between inputs, how does a firm determine which of the possible combinations to use?

Determining the Optimal Input Mix

If several alternative input combinations can be used to produce the optimal level of output, a profit-maximizing firm will select the input combination with the lowest cost. This process is known as cost minimization.

Cost Minimization

How does a firm determine the combination of inputs that maximizes profits? Let’s consider this question using an example.

Imagine you manage a grocery store chain and you need to decide the right combination of self-checkout stations and cashiers at a new store. Table 43-1 shows the alternative combinations of capital (self-checkout stations) and labor (cashiers) you can hire to check out customers shopping at the store. If the store puts in 20 self-checkout stations, you will need to hire 1 cashier to monitor every 5 stations for a total of 4 cashiers. However, trained cashiers are faster than customers at scanning goods, so the store could check out the same number of customers using 10 cashiers and only 10 self-checkout stations.

If you can check out the same number of customers using either of these combinations of capital and labor, how do you decide which combination of inputs to use? By finding the input combination that costs the least—the cost-minimizing input combination.

Assume that the cost to rent, operate, and maintain a self-checkout station for a month is $1,000 and hiring a cashier costs $1,600 per month. The cost of each input combination from Table 43-1 is shown below.

What is the right combination of cashiers and self-checkout stations?

Aleph Studio/Shutterstock

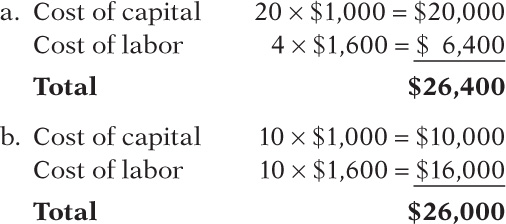
Clearly, your firm would choose the lower cost combination, combination b, and hire 10 cashiers and put in 10 self-checkout stations.

When firms must choose between alternative combinations of inputs, they evaluate the cost of each combination and select the one that minimizes the cost of production. This can be done by calculating the total cost of each alternative combination of inputs, as shown in this example. However, because the number of possible combinations can be very large, it is more practical to use marginal analysis to find the cost-minimizing level of output—which brings us to the cost-minimization rule.

The Cost-Minimization Rule

We already know that the additional output that results from hiring an additional unit of an input is the marginal product (MP) of that input. Firms want to receive the highest possible marginal product from each dollar spent on inputs. To do this, firms adjust their hiring of inputs until the marginal product per dollar is equal for all inputs. This is the cost-minimization rule. When the inputs are labor and capital, this amounts to equating the marginal product of labor (MPL) per dollar spent on wages to the marginal product of capital (MPK) per dollar spent to rent capital:

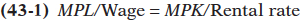
To understand why cost minimization occurs when the marginal product per dollar is equal for all inputs, let’s start by looking at two counterexamples. Consider a situation in which the marginal product of labor per dollar is greater than the marginal product of capital per dollar. This situation is described by Equation 43-2:

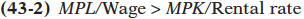
Suppose the marginal product of labor is 20 units and the marginal product of capital is 100 units. If the wage is $10 and the rental rate for capital is $100, then the marginal product per dollar will be 20/$10 = 2 units of output per dollar for labor and 100/$100 = 1 unit of output per dollar for capital. The firm is receiving 2 additional units of output for each dollar spent on labor and only 1 additional unit of output for each dollar spent on capital. In this case, the firm gets more additional output for its money by hiring labor, so it should hire more labor and less capital.

Because of diminishing returns, as the firm hires more labor, the marginal product of labor falls and as it hires less capital, the marginal product of capital rises. The firm will continue to substitute labor for capital until the falling marginal product of labor per dollar meets the rising marginal product of capital per dollar and the two are equivalent. That is, the firm will adjust its hiring of capital and labor until the marginal product per dollar spent on each input is equal, as in Equation 43-1.

Next, consider a situation in which the marginal product of capital per dollar is greater than the marginal product of labor per dollar. This situation is described by Equation 43-3:

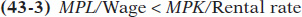
Let’s continue with the assumption that the marginal product of labor for the last unit of labor hired is 20 units and the marginal product of capital for the last unit of capital hired is 100 units. If the wage is $10 and the rental rate for capital is $25, then the marginal product per dollar will be 20/$10 = 2 units of output per dollar for labor and 100/$25 = 4 units of output per dollar for capital. The firm is receiving 4 additional units of output for each dollar spent on capital and only 2 additional units of output for each dollar spent on labor. In this case, the firm gets more additional output for its money by hiring capital, so it should hire more capital and less labor.

Because of diminishing returns, as the firm hires more capital, the marginal product of capital falls, and as it hires less labor, the marginal product of labor rises. The firm will continue to hire more capital and less labor until the falling marginal product of capital per dollar meets the rising marginal product of labor per dollar to satisfy the cost-minimization rule. That is, the firm will adjust its hiring of capital and labor until the marginal product per dollar spent on each input is equal.

The cost-minimization rule is analogous to the optimal consumption rule (introduced in the module on maximizing utility): consumers maximize their utility by choosing the combination of goods so that the marginal utility per dollar is equal for all goods.

Module 43 Review

Check Your Understanding