1.2 44The Time Value of Money

WHAT YOU WILL LEARN
 Why a dollar today is worth more than a dollar a year from now
Why a dollar today is worth more than a dollar a year from now
 How the concept of present value can help you make decisions when costs or benefits occur in the future
How the concept of present value can help you make decisions when costs or benefits occur in the future
The Concept of Present Value
Individuals are often faced with financial decisions that will have consequences long into the future. For example, when you decide to attend college, you are committing yourself to years of study, which you expect will pay off for the rest of your life. So the decision to attend college is a decision to embark on a long-
The basic rule in deciding whether or not to undertake a project is that you should compare the benefits of that project with its costs, implicit as well as explicit. But making these comparisons can sometimes be difficult because the benefits and costs of a project may not arrive at the same time.
Sometimes the costs of a project come at an earlier date than the benefits. For example, going to college involves large immediate costs: tuition, income forgone because you are in school, and so on. The benefits, such as a higher salary in your future career, come later, often much later. In other cases, the benefits of a project come at an earlier date than the costs. If you take out a loan to pay for a vacation cruise, the satisfaction of the vacation will come immediately, but the burden of making payments will come later.
How, specifically is time an issue in economic decision making?
Borrowing, Lending, and Interest
In general, having a dollar today is worth more than having a dollar a year from now. To see why, let’s consider two examples.
First, suppose that you get a new job that comes with a $1,000 bonus, which will be paid at the end of the first year. But you would like to spend the extra money now—
The answer is yes—
Now consider a different scenario. Suppose that you are paid a bonus of $1,000 today, and you decide that you don’t want to spend the money until a year from now. What do you do with it? You may decide to put it in the bank; in effect, you would be lending the $1,000 to the bank, which in turn lends it out to its customers who wish to borrow. At the end of a year, you will get more than $1,000 back—
All of this means that having $1,000 today is worth more than having $1,000 a year from now. As any borrower and lender know, this is what allows a lender to charge a borrower interest on a loan: borrowers are willing to pay interest in order to have money today rather than waiting until they acquire that money later on.
Most interest rates are stated as the percentage of the borrowed amount that must be paid to the lender for each year of the loan. Whether money is actually borrowed for 1 month or 10 years, and regardless of the amount, the same principle applies: money in your pocket today is worth more than money in your pocket tomorrow. To keep things simple in the discussions that follow, we’ll restrict ourselves to examples of 1-
Because the value of money depends on when it is paid or received, you can’t evaluate a project by simply adding up the costs and benefits when those costs and benefits arrive at different times. You must take time into account when evaluating the project because $1 that is paid to you today is worth more than $1 that is paid to you a year from now. Similarly, $1 that you must pay today is more burdensome than $1 that you must pay next year.
Fortunately, there is a simple way to adjust for these complications so that we can correctly compare the value of dollars received and paid out at different times.
Next we’ll see how the interest rate can be used to convert future benefits and costs into what economists call present values. By using present values when evaluating a project, you can evaluate a project as if all relevant costs and benefits were occurring today rather than at different times. This allows people to “factor out” the complications created by time. We’ll start by defining the concept of present value.
Defining Present Value
The key to the concept of present value is to understand that you can use the interest rate to compare the value of a dollar realized today with the value of a dollar realized later. Why the interest rate? Because the interest rate correctly measures the cost to you of delaying the receipt of a dollar of benefit and, correspondingly, the benefit to you of delaying the payment of a dollar of cost.

Let’s illustrate this with some examples.
Suppose that you are evaluating whether or not to take a job in which your employer promises to pay you a bonus at the end of the first year. What is the value to you today of $1 of bonus money to be paid one year in the future? A slightly different way of asking the same question: what amount would you be willing to accept today as a substitute for receiving $1 one year from now?
To answer this question, begin by observing that you need less than $1 today in order to be assured of having $1 one year from now. Why? Because any money that you have today can be lent out at interest—
Let’s work this out mathematically. We’ll use the symbol r to represent the interest rate, expressed in decimal terms—

The next step is to find out how much you would have to lend out today to have $1 a year from now. To do that, we just need to set Equation 44-
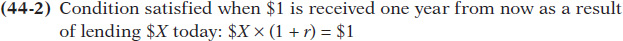
Rearranging Equation 44-
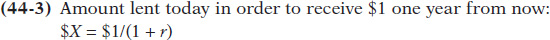
This means that you would be willing to accept today the amount $X defined by Equation 44-
Now let’s solve Equation 44-
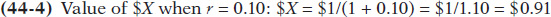
The present value of $1 realized one year from now is equal to $1/(1 + r): the amount of money you must lend out today in order to have $1 in one year. It is the value to you today of $1 realized one year from now.
So you would be willing to accept $0.91 today in exchange for every $1 to be paid to you one year from now. Economists have a special name for $X—it’s called the present value of $1. Note that the present value of any given amount will change as the interest rate changes.
To see that this technique works for evaluating future costs as well as evaluating future benefits, consider the following example. Suppose you enter into an agreement that obliges you to pay $1 one year from now—

These examples show us that the present value concept provides a way to calculate the value today of $1 that is realized in a year—
Below we will use the present value concept to evaluate a project. But before we do that, it is worthwhile to note that the present value method can be used for projects in which the $1 is realized more than a year later—
Let’s call $ V the amount of money you need to lend today at an interest rate of r in order to have $1 in two years. So if you lend $V today, you will receive $V × (1 + r) in one year. And if you relend that sum for another year, you will receive $V × (1 + r) × (1 + r) = $ V × (1 + r)2 at the end of the second year. At the end of two years, $V will be worth $V × (1 + r)2. In other words:
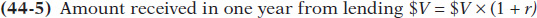
Amount received in two years from lending $V = $V × (1 + r) × (1 + r) = $V × (1 + r)2 and so on. For example, if r = 0.10, then $V × (1.10)2 = $V × 1.21.
Now we are ready to answer the question of what $1 realized two years in the future is worth today. In order for the amount lent today, $V, to be worth $1 two years from now, it must satisfy this formula:

Rearranging Equation 44-
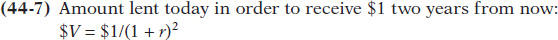
Given r = 0.10 and using Equation 44-

From this example we can see how the present value concept can be expanded to a number of years even greater than two. If we ask what the present value is of $1 realized any number of years, represented by N, into the future, the answer is given by a generalization of the present value formula: it is equal to $1/(1 + r)N.
Using Present Value
Suppose you have to choose one of three hypothetical projects to undertake. Project A costs nothing and has an immediate payoff to you of $ 100. Project B requires that you pay $10 today in order to receive $115 a year from now. Project C gives you an immediate payoff of $119 but requires that you pay $20 a year from now. We’ll assume that the annual interest rate is 10%—that is, r = 0.10.
The net present value of a project is the present value of current and future benefits minus the present value of current and future costs.
The problem in evaluating these three projects is that their costs and benefits are realized at different times. That is, of course, where the concept of present value becomes extremely helpful: by using present value to convert any dollars realized in the future into today’s value, you factor out the issue of time. Appropriate comparisons can be made using the net present value of a project—
Table 44-1 shows how to calculate net present value for each of the three projects. The second and third columns show how many dollars are realized and when they are realized; costs are indicated by a minus sign. The fourth column shows the equations used to convert the flows of dollars into their present value, and the fifth column shows the actual amounts of the total net present value for each of the three projects.
44-1
The Net Present Value of Three Hypothetical Projects
| Project | Dollars realized today | Dollars realized one year from today | Present value formula | Net present value given r = 0.10 |
|---|---|---|---|---|
| A | $100 | — | $100 | $100.00 |
| B | −$10 | $115 | −$10 + $115/(1 + r) | $94.55 |
| C | $119 | −$20 | 119 − $20/(1 + r) | $100.82 |
For instance, to calculate the net present value of project B, we need to calculate the present value of $115 received in one year. The present value of $1 received in one year would be $1/(1 + r). So the present value of $115 is equal to 115 × $1/(1 + r); that is, $115/(1 + r). The net present value of project B is the present value of today’s and future benefits minus the present value of today’s and future costs: $10 + $115/(1 + r).
From the fifth column, we can immediately see which is the preferred project—
This example shows how important the concept of present value is. If we had failed to use the present value calculations and instead simply added up the dollars generated by each of the three projects, we could have easily been misled into believing that project B was the best project and project C was the worst.
HOW BIG IS THAT JACKPOT, ANYWAY?
For a clear example of present value at work, consider the case of lottery jackpots.
On March 30, 2012, Mega Millions set the record for the largest jackpot ever in North America, with a payout of $656 million. Well, sort of. That $656 million was available only if you chose to take your winnings in the form of an “annuity,” consisting of an annual payment for the next 26 years. If you wanted cash up front, the jackpot was only $474 million and change.

Why was Mega Millions so stingy about quick payoffs? It was all a matter of present value. If the winner had been willing to take the annuity, the lottery would have invested the jackpot money, buying U.S. government bonds (in effect lending the money to the federal government). The money would have been invested in such a way that the investments would pay just enough to cover the annuity. This worked, of course, because at the interest rates prevailing at the time, the present value of a $656 million annuity spread over 26 years was just about $474 million. To put it another way, the opportunity cost to the lottery of that annuity in present value terms was $474 million.
So why didn’t they just call it a $474 million jackpot? Well, $656 million sounds more impressive! But receiving $656 million over 26 years is essentially the same as receiving $474 million today.
44
Solutions appear at the back of the book.
Check Your Understanding
1. Consider the three hypothetical projects shown in Table 44-1. This time, however, suppose that the interest rate is only 2%.
-
a. Calculate the net present values of the three projects. Which one is now preferred?
The net present value of project A is unaffected by the interest rate since it is money received today; its present value is still $100. The net present value of project B is now −$10 + $115/1.02 = $102.75. The net present value of project C is now $119 − $20/1.02 = $99.39. Project B is now preferred. -
b. Explain why the preferred choice with a 2% interest rate differs from one with a 10% interest rate.
When the interest rate is lower, the cost of waiting for money that arrives in the future is lower. For example, at a 10% interest rate, $1 arriving one year from today is worth only $1/1.10 = $0.91. But when the interest rate is 2%, $1 arriving one year from today is worth $1/1.02 = $0.98, a sizable increase. As a result, project B, which has a benefit one year from today, becomes more attractive. And project C, which has a cost one year from today, becomes less attractive.
Multiple-
Question
1. Suppose, for simplicity, that a bank uses a single interest rate for loans and deposits, there is no inflation, and all unspent money is deposited in the bank. The interest rate measures which of the following?
I. the cost of using a dollar today rather than a year from now
II. the benefit of delaying the use of a dollar from today until a year from now
III. the price of borrowing money calculated as a percentage of the amount borrowed
| A. |
| B. |
| C. |
| D. |
| E. |
Question
2. If the interest rate is zero, then the present value of a dollar received at the end of the year is
| A. |
| B. |
| C. |
| D. |
| E. |
Question
3. If the interest rate is 10%, the present value of $1 paid to you one year from now is
| A. |
| B. |
| C. |
| D. |
| E. |
Question
4. If the interest rate is 5%, the amount received one year from now as a result of lending $100 today is
| A. |
| B. |
| C. |
| D. |
| E. |
Question
5. What is the present value of $100 realized two years from now if the interest rate is 10%?
| A. |
| B. |
| C. |
| D. |
| E. |
Critical-
1. What is the amount you will receive in three years if you loan $1,000 at 5% interest?
2. What is the present value of $1,000 received in three years if the interest rate is 5%?