Optimal Consumption Choice

A consumer’s optimal consumption bundle is the consumption bundle that maximizes the consumer’s total utility given his or her budget constraint.

Because Sammy has a budget constraint, which means that he will consume a consumption bundle on the budget line, a choice to consume a given quantity of clams also determines his potato consumption, and vice versa. We want to find the consumption bundle—the point on the budget line—that maximizes Sammy’s total utility. This bundle is Sammy’s optimal consumption bundle, the consumption bundle that maximizes his total utility given the budget constraint.

Table 10-1 shows how much utility Sammy gets from different levels of consumption of clams and potatoes, respectively. According to the table, Sammy has a healthy appetite; the more of either good he consumes, the higher his utility.

Utility from clam consumption

Utility from potato consumption

Quantity of clams (pounds)

Utility from clams (utils)

Quantity of potatoes (pounds)

Utility from potatoes (utils)

0

  0

  0

0

1

15

  1

11.5

2

25

  2

21.4

3

31

  3

29.8

4

34

  4

36.8

5

36

  5

42.5
   

  6

47.0
   

  7

50.5
   

  8

53.2
   

  9

55.2
   

10

56.7
Table :

TABLE 10-1 Sammy’s Utility from Clam and Potato Consumption

But because he has a limited budget, he must make a trade-off: the more pounds of clams he consumes, the fewer pounds of potatoes, and vice versa. That is, he must choose a point on his budget line.

Table 10-2 shows how his total utility varies for the different consumption bundles along his budget line. Each of six possible consumption bundles, A through F from Figure 10-2, is given in the first column. The second column shows the level of clam consumption corresponding to each choice. The third column shows the utility Sammy gets from consuming those clams. The fourth column shows the quantity of potatoes Sammy can afford given the level of clam consumption; this quantity goes down as his clam consumption goes up, because he is sliding down the budget line. The fifth column shows the utility he gets from consuming those potatoes. And the final column shows his total utility. In this example, Sammy’s total utility is the sum of the utility he gets from clams and the utility he gets from potatoes.

Consumption bundle

Quantity of clams (pounds)

Utility from clams (utils)

Quantity of potatoes (pounds)

Utility from potatoes (utils)

Total utility (utils)

A

0

  0

10

56.7

56.7

B

1

15

  8

53.2

68.2

C

2

25

  6

47.0

72.0

D

3

31

  4

36.8

67.8

E

4

34

  2

21.4

55.4

F

5

36

  0

0

36.0
Table :

TABLE 10-2 Sammy’s Budget and Total Utility

Figure 10-3 gives a visual representation of the data shown in Table 10-2. Panel (a) shows Sammy’s budget line, to remind us that when he decides to consume more clams he is also deciding to consume fewer potatoes. Panel (b) then shows how his total utility depends on that choice. The horizontal axis in panel (b) has two sets of labels: it shows both the quantity of clams, increasing from left to right, and the quantity of potatoes, increasing from right to left.

Optimal Consumption Bundle Panel (a) shows Sammy’s budget line and his six possible consumption bundles. Panel (b) shows how his total utility is affected by his consumption bundle, which must lie on his budget line. The quantity of clams is measured from left to right on the horizontal axis, and the quantity of potatoes is measured from right to left. His total utility is maximized at bundle C, the highest point on his utility function, where he consumes 2 pounds of clams and 6 pounds of potatoes. This is Sammy’s optimal consumption bundle.

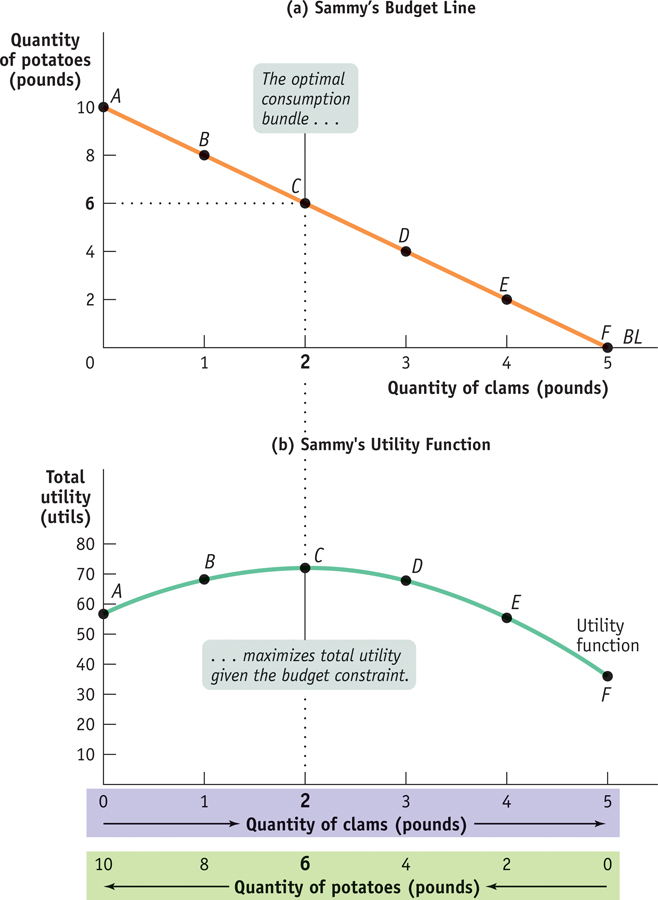
The reason we can use the same axis to represent consumption of both goods is, of course, the budget line: the more pounds of clams Sammy consumes, the fewer pounds of potatoes he can afford, and vice versa.

Clearly, the consumption bundle that makes the best of the trade-off between clam consumption and potato consumption, the optimal consumption bundle, is the one that maximizes Sammy’s total utility. That is, Sammy’s optimal consumption bundle puts him at the highest point of the total utility curve.

As always, we can find the highest point of the curve by direct observation. We can see from Figure 10-3 that Sammy’s total utility is maximized at point C—that his optimal consumption bundle contains 2 pounds of clams and 6 pounds of potatoes. But we know that we usually gain more insight into “how much” problems when we use marginal analysis. So in the next section we turn to representing and solving the optimal consumption choice problem with marginal analysis.

FOR INQUIRING MINDS: Food for Thought on Budget Constraints

Budget constraints aren’t just about money. In fact, there are many other budget constraints affecting our lives. You face a budget constraint if you have a limited amount of closet space for your clothes. All of us face a budget constraint on time: there are only so many hours in the day.

And people trying to lose weight on the Weight Watchers plan face a budget constraint on the foods they eat.

The Weight Watchers plan assigns each food a certain number of points. A 4-ounce scoop of premium ice cream is 8 points, a slice of cheese pizza with a medium crust is 7 points, and a cup of grapes is zero points. You are allowed a maximum number of points each day but are free to choose which foods you eat.

In other words, a dieter on the Weight Watchers plan is just like a consumer choosing a consumption bundle: points are the equivalent of prices, and the overall point limit is the equivalent of total income.

ECONOMICS in Action: The Great Condiment Craze

The Great Condiment Craze

Changing tastes and budgets drove the American condiment craze.
The Photo Works

Those of us of a certain age remember when the only kind of mustard available in American grocery stores was a runny, fluorescent yellow concoction packaged in plastic squeeze bottles. Ditto for ketchup and mayonnaise—what little selection there was, tasted the same. As for salsa—wasn’t that some sort of dance step?

No longer. Americans have developed an intense liking for condiments—in a dizzying array of varieties. Who wants plain mustard when you can get mustard flavored with roasted garlic, apricot, or even bourbon/molasses? Likewise, would you like saffron and garlic mayonnaise or sriracha mayonnaise on your club sandwich? And sales of salsa in the United States have long since overtaken ketchup sales.

So what happened? Tastes changed and budgets changed. Spurred by the severe recession that began in 2007, more budget-minded consumers ate at home. But having been exposed to gourmet cooking and ethnic cuisine, they sought ways to spice up their home cooking. Unsurprisingly, then, the onset of the recession coincided with an increase of condiment sales of 5.6% in 2008 and 6.2% in 2009. By 2012, U.S. condiment sales reached $9.7 billion, and have been forecast to reach $10.7 billion by 2017.

The explosion of varieties stems from the fact that it’s fairly easy to make bottled condiments. This enables smaller companies to experiment with exotic flavors, finding the ones that appeal to consumers’ increasingly sophisticated tastes. Eventually, the flavors that attract a significant following are picked up by the larger companies such as Kraft. As one industry analyst put it, “People want cheaper, more specialized gourmet products. It’s like fashion.”

As the economy has slowly recovered in recent years, restaurant dining has picked up. However, American home cooking appears to have been forever changed by the great condiment craze. Consumers continue to purchase a wide variety of premium condiments to add zest to their home-cooked meals.

Quick Review

  • The budget constraint requires that a consumer’s total expenditure be no more than his or her income. The set of consumption bundles that satisfy the budget constraint is the consumer’s consumption possibilities.

  • A consumer who spends all of his or her income chooses a point on his or her budget line. The budget line slopes downward because on the budget line a consumer must consume less of one good in order to consume more of another.

  • The consumption choice that maximizes total utility given the consumer’s budget constraint is the optimal consumption bundle. It must lie on the consumer’s budget line.

10-2

  1. Question 10.4

    In the following two examples, find all the consumption bundles that lie on the consumer’s budget line. Illustrate these consumption possibilities in a diagram and draw the budget line through them.

    1. The consumption bundle consists of movie tickets and buckets of popcorn. The price of each ticket is $10.00, the price of each bucket of popcorn is $5.00, and the consumer’s income is $20.00. In your diagram, put movie tickets on the vertical axis and buckets of popcorn on the horizontal axis.

    2. The consumption bundle consists of underwear and socks. The price of each pair of underwear is $4.00, the price of each pair of socks is $2.00, and the consumer’s income is $12.00. In your diagram, put pairs of socks on the vertical axis and pairs of underwear on the horizontal axis.

Solutions appear at back of book.