We’ve already introduced the concept of marginal utility, the additional utility a consumer gets from consuming one more unit of a good or service; now let’s see how this concept can be used to derive the related measure of marginal utility per dollar.

Table 10-3 shows how to calculate the marginal utility per dollar spent on clams and potatoes, respectively.

In panel (a) of the table, the first column shows different possible amounts of clam consumption. The second column shows the utility Sammy derives from each amount of clam consumption; the third column then shows the marginal utility, the increase in utility Sammy gets from consuming an additional pound of clams. Panel (b) provides the same information for potatoes. The next step is to derive marginal utility per dollar for each good. To do this, we must divide the marginal utility of the good by its price in dollars.

To see why we must divide by the price, compare the third and fourth columns of panel (a). Consider what happens if Sammy increases his clam consumption from 2 pounds to 3 pounds. As we can see, this increase in clam consumption raises his total utility by 6 utils. But he must spend $4 for that additional pound, so the increase in his utility per additional dollar spent on clams is 6 utils/$4 = 1.5 utils per dollar.

Similarly, if he increases his clam consumption from 3 pounds to 4 pounds, his marginal utility is 3 utils but his marginal utility per dollar is 3 utils/$4 = 0.75 util per dollar. Notice that because of diminishing marginal utility, Sammy’s marginal utility per pound of clams falls as the quantity of clams he consumes rises. As a result, his marginal utility per dollar spent on clams also falls as the quantity of clams he consumes rises.

So the last column of panel (a) shows how Sammy’s marginal utility per dollar spent on clams depends on the quantity of clams he consumes. Similarly, the last column of panel (b) shows how his marginal utility per dollar spent on potatoes depends on the quantity of potatoes he consumes. Again, marginal utility per dollar spent on each good declines as the quantity of that good consumed rises, because of diminishing marginal utility.

We will use the symbols MU_C and MU_P to represent the marginal utility per pound of clams and potatoes, respectively. And we will use the symbols P_C and P_P to represent the price of clams (per pound) and the price of potatoes (per pound). Then the marginal utility per dollar spent on clams is MU_C/P_C and the marginal utility per dollar spent on potatoes is MU_P/P_P. In general, the additional utility generated from an additional dollar spent on a good is equal to:

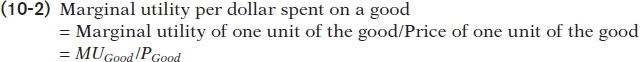
Now let’s see how this concept helps us derive a consumer’s optimal consumption using marginal analysis.