Consider Noelle, who runs a Christmas tree farm. Suppose that the market price of Christmas trees is $18 per tree and that Noelle is a price-taker—she can sell as many as she likes at that price. Then we can use the data in Table 12-1 to find her profit-maximizing level of output by direct calculation.

The first column shows the quantity of output in number of trees, and the second column shows Noelle’s total revenue from her output: the market value of trees she produced. Total revenue, TR, is equal to the market price multiplied by the quantity of output:

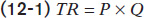
In this example, total revenue is equal to $18 per tree times the quantity of output in trees.

The third column of Table 12-1 shows Noelle’s total cost. The fourth column shows her profit, equal to total revenue minus total cost:

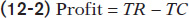
As indicated by the numbers in the table, profit is maximized at an output of 50 trees, where profit is equal to $180. But we can gain more insight into the profit-maximizing choice of output by viewing it as a problem of marginal analysis, a task we’ll do next.