The Monopolist’s Profit-Maximizing Output and Price
PITFALLS: FINDING THE MONOPOLY PRICE
FINDING THE MONOPOLY PRICE
In order to find the profit-
However, it’s important not to fall into a common error: imagining that point A also shows the price at which the monopolist sells its output. It doesn’t: it shows the marginal revenue received by the monopolist, which we know is less than the price.
To find the monopoly price, you have to go up vertically from A to the demand curve. There you find the price at which consumers demand the profit-
To complete the story of how a monopolist maximizes profit, we now bring in the monopolist’s marginal cost. Let’s assume that there is no fixed cost of production; we’ll also assume that the marginal cost of producing an additional diamond is constant at $200, no matter how many diamonds De Beers produces. Then marginal cost will always equal average total cost, and the marginal cost curve (and the average total cost curve) is a horizontal line at $200, as shown in Figure 13-6.
To maximize profit, the monopolist compares marginal cost with marginal revenue. If marginal revenue exceeds marginal cost, De Beers increases profit by producing more; if marginal revenue is less than marginal cost, De Beers increases profit by producing less. So the monopolist maximizes its profit by using the optimal output rule:
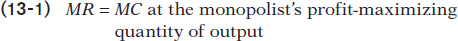
13-6
The Monopolist’s Profit-

The monopolist’s optimal point is shown in Figure 13-6. At A, the marginal cost curve, MC, crosses the marginal revenue curve, MR. The corresponding output level, 8 diamonds, is the monopolist’s profit-