What is the cost of a tax? You might be inclined to answer that it is the money taxpayers pay to the government. In other words, you might believe that the cost of a tax is the tax revenue collected. But suppose the government uses the tax revenue to provide services that taxpayers want. Or suppose that the government simply hands the tax revenue back to taxpayers. Would we say in those cases that the tax didn’t actually cost anything?

No—because a tax, like a quota, prevents mutually beneficial transactions from occurring. Consider Figure 7-6 once more. Here, with a $40 tax on hotel rooms, guests pay $100 per room but hotel owners receive only $60 per room. Because of the wedge created by the tax, we know that some transactions don’t occur that would have occurred without the tax.

For example, we know from the supply and demand curves that there are some potential guests who would be willing to pay up to $90 per night and some hotel owners who would be willing to supply rooms if they received at least $70 per night. If these two sets of people were allowed to trade with each other without the tax, they would engage in mutually beneficial transactions—hotel rooms would be rented.

But such deals would be illegal, because the $40 tax would not be paid. In our example, 5,000 potential hotel room rentals that would have occurred in the absence of the tax, to the mutual benefit of guests and hotel owners, do not take place because of the tax.

So an excise tax imposes costs over and above the tax revenue collected in the form of inefficiency, which occurs because the tax discourages mutually beneficial transactions. As we learned in Chapter 5, the cost to society of this kind of inefficiency—the value of the forgone mutually beneficial transactions—is called the deadweight loss. While all real-world taxes impose some deadweight loss, a badly designed tax imposes a larger deadweight loss than a well-designed one.

To measure the deadweight loss from a tax, we turn to the concepts of producer and consumer surplus. Figure 7-8 shows the effects of an excise tax on consumer and producer surplus. In the absence of the tax, the equilibrium is at E and the equilibrium price and quantity are P_E and Q_E, respectively. An excise tax drives a wedge equal to the amount of the tax between the price received by producers and the price paid by consumers, reducing the quantity sold. In this case, where the tax is T dollars per unit, the quantity sold falls to Q_T. The price paid by consumers rises to P_C, the demand price of the reduced quantity, Q_T, and the price received by producers falls to P_P, the supply price of that quantity. The difference between these prices, P_C – P_P, is equal to the excise tax, T.

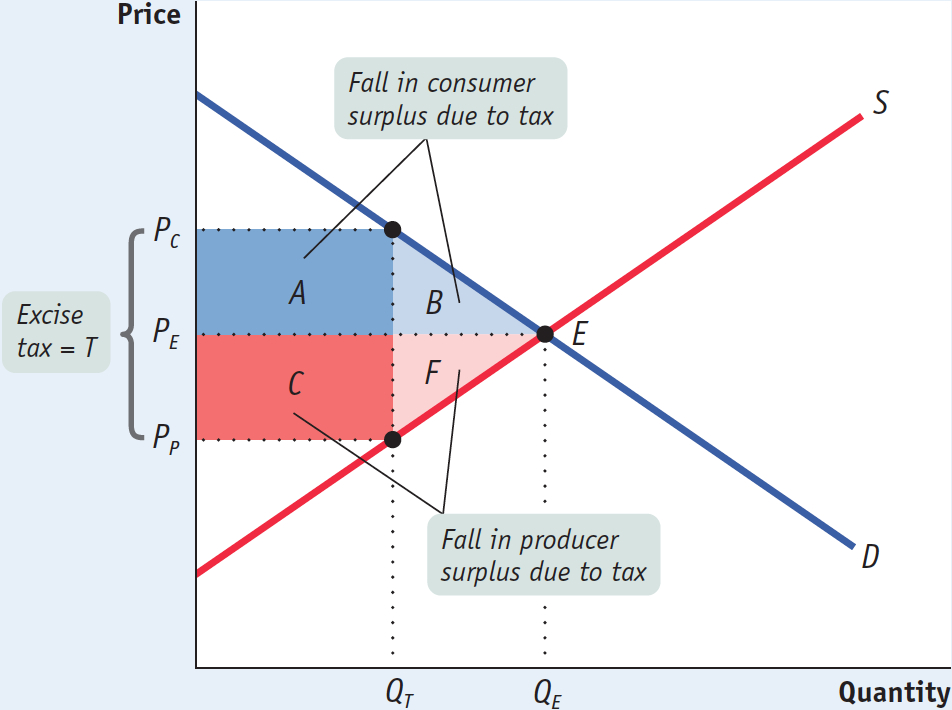
Using the concepts of producer and consumer surplus, we can show exactly how much surplus producers and consumers lose as a result of the tax. From Figure 5-4 we learned that a fall in the price of a good generates a gain in consumer surplus that is equal to the sum of the areas of a rectangle and a triangle. Similarly, a price increase causes a loss to consumers that is represented by the sum of the areas of a rectangle and a triangle. So it’s not surprising that in the case of an excise tax, the rise in the price paid by consumers causes a loss equal to the sum of the areas of a rectangle and a triangle: the dark blue rectangle labeled A and the area of the light blue triangle labeled B in Figure 7-8.

Meanwhile, the fall in the price received by producers leads to a fall in producer surplus. This, too, is equal to the sum of the areas of a rectangle and a triangle. The loss in producer surplus is the sum of the areas of the dark red rectangle labeled C and the pink triangle labeled F in Figure 7-8.

Of course, although consumers and producers are hurt by the tax, the government gains revenue. The revenue the government collects is equal to the tax per unit sold, T, multiplied by the quantity sold, Q_T. This revenue is equal to the area of a rectangle Q_T wide and T high. And we already have that rectangle in the figure: it is the sum of rectangles A and C. So the government gains part of what consumers and producers lose from an excise tax.

But a portion of the loss to producers and consumers from the tax is not offset by a gain to the government—specifically, the two triangles B and F. The deadweight loss caused by the tax is equal to the combined area of these two triangles. It represents the total surplus lost to society because of the tax—that is, the amount of surplus that would have been generated by transactions that now do not take place because of the tax.

Figure 7-9 is a version of Figure 7-8 that leaves out rectangles A (the surplus shifted from consumers to the government) and C (the surplus shifted from producers to the government) and shows only the deadweight loss, here drawn as a triangle shaded yellow. The base of that triangle is equal to the tax wedge, T; the height of the triangle is equal to the reduction in the quantity transacted due to the tax, Q_E – Q_T Clearly, the larger the tax wedge and the larger the reduction in the quantity transacted, the greater the inefficiency from the tax.

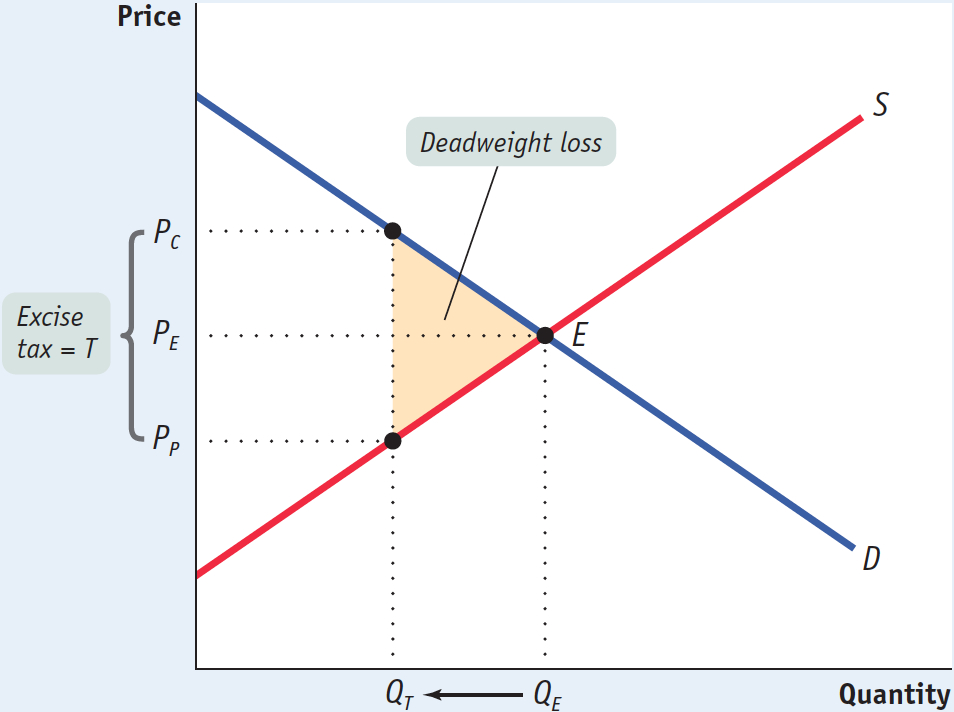
But also note an important, contrasting point: if the excise tax somehow didn’t reduce the quantity bought and sold in this market—if Q_T remained equal to Q_E after the tax was levied—the yellow triangle would disappear and the deadweight loss from the tax would be zero. This observation is simply the flip-side of the principle found earlier in the chapter: a tax causes inefficiency because it discourages mutually beneficial transactions between buyers and sellers. So if a tax does not discourage transactions, which would be true if either supply or demand were perfectly inelastic, it causes no deadweight loss. In this case, the tax simply shifts surplus straight from consumers and producers to the government.

Using a triangle to measure deadweight loss is a technique used in many economic applications. For example, triangles are used to measure the deadweight loss produced by types of taxes other than excise taxes. They are also used to measure the deadweight loss produced by monopoly, another kind of market distortion. And deadweight-loss triangles are often used to evaluate the benefits and costs of public policies besides taxation—such as whether to impose stricter safety standards on a product.

In considering the total amount of inefficiency caused by a tax, we must also take into account something not shown in Figure 7-9: the resources actually used by the government to collect the tax, and by taxpayers to pay it, over and above the amount of the tax. These lost resources are called the administrative costs of the tax. The most familiar administrative cost of the U.S. tax system is the time individuals spend filling out their income tax forms or the money they pay for tax return preparation services like those provided by H&R Block and companies like it. (The latter is considered an inefficiency from the point of view of society because resources spent on return preparation could be used for other, non-tax-related purposes.)

Included in the administrative costs that taxpayers incur are resources used to evade the tax, both legally and illegally. The costs of operating the Internal Revenue Service, the arm of the federal government tasked with collecting the federal income tax, are actually quite small in comparison to the administrative costs paid by taxpayers.

So the total inefficiency caused by a tax is the sum of its deadweight loss and its administrative costs. The general rule for economic policy is that, other things equal, a tax system should be designed to minimize the total inefficiency it imposes on society. In practice, other considerations also apply (as the Washington administration learned during the Whiskey Rebellion), but this principle nonetheless gives valuable guidance. Administrative costs are usually well known, more or less determined by the current technology of collecting taxes (for example, filing paper returns versus filing electronically). But how can we predict the size of the deadweight loss associated with a given tax? Not surprisingly, as in our analysis of the incidence of a tax, the price elasticities of supply and demand play crucial roles in making such a prediction.